求根公式的再理解及其教育价值
华南师范大学数学科学学院(510631) 卢颖妍
求根公式的再理解及其教育价值
华南师范大学数学科学学院(510631) 卢颖妍
1.引言
求根公式的发展经过了漫长的岁月,现在求根公式作为初中教材的求解一元二次方程的有力手段.但是在初中的数学教学中,很多老师对于求根公式的教学往往只停留在对公式的表面理解,要求学生死板记忆公式,懂得应用公式求解一元二次方程即可,让很多学生对求根公式产生一种难记难懂的感觉,使得更多人认为数学就是一些枯燥无味的公式.为尽量改变这些片面的观念,本文将从求根公式的推导、几何解释、自身特征几个方面让更多人重新认识求根公式,发现求根公式的美,真正体会求根公式的教育价值.
2.求根公式的推导过程
对于人教版初中教材[1]上的求根公式的推导主要运用了配方法以及降次思想.设计意图是由于学生前面刚刚学完配方法,容易想到将二次项系数化为1,利用配方法转化为可直接开方的形式,问题难在推导过程中对式子b2-4ac涉及了分类讨论的思想.教材中的推导过程如下(方法1):
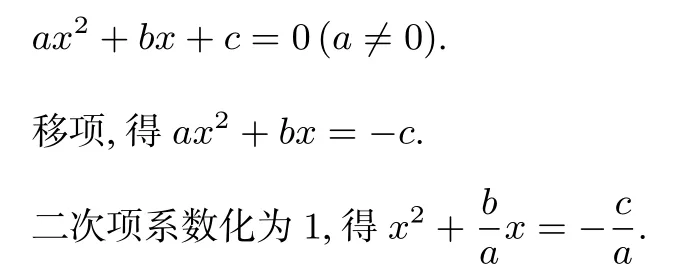
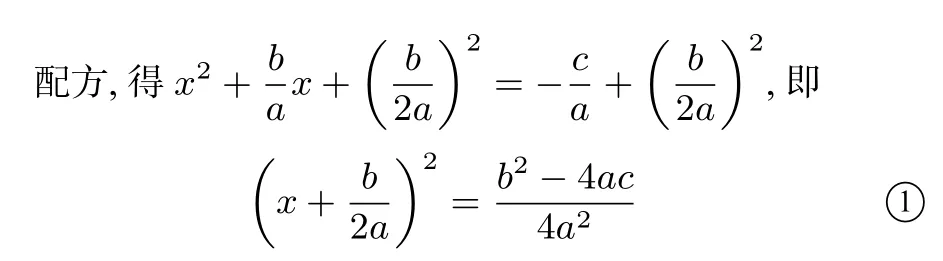
(3)b2-4ac<0,方程无实数根.
以上是初中教材中的求根公式的推导过程,现在如果已经知道了一元二次方程的求根公式为我们可以从公式本身出发,对一元二次方程和它的求解逆向思考,由有
两边平方,
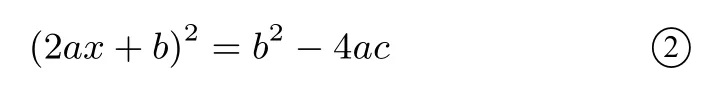
这里每一步都是平淡的,但是,当我们把上述每一步骤倒过来书写时,我们就“发现”了一元二次方程的一个新解法[2](方法2):
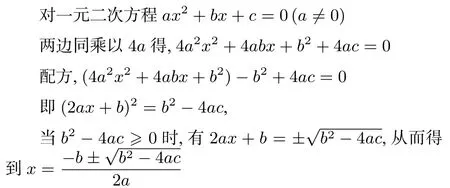
与课本中的解法相比,这个解法有两个明显的优点:
第一,解法2左右两边同乘以4a比解法1中两边除以a之后的配方法更简易了,消除了的误解.解法1中容易让学生产生误解
小结:从求根公式的两种不同的推论过程可以看出它各自具有一定的教育价值:
(1)在思想方法上,教材上的解法(解法1)运用了配方法,其基本思想是降次,通过配方转化为可以直接开方的形式,推导过程中涉及分类讨论的思想以及方程的思想,同时整体思路是转化为学生已经学过的配方法求解,这同时体现了转化与化归思想.
3.求根公式的几何解释
在初中的课本中,我们从来没有接触过求根公式的几何解释,甚至很少人知道求根公式竟然也可以向完全平方公式和平方差公式一样用几何图形解释.在初中,我们知道完全平方公式的几何解释如下:
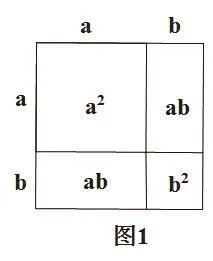
图1
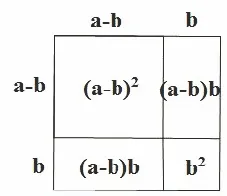
图2
从图1中我们可以容易知道:(a±b)2=a2±2ab+b2.从图2中我们可以容易知道:(a-b)2=a2-2ab+b2我们也知道平方差公式也可以用下面的几何图形解释:
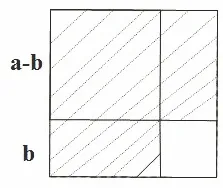
图3


图4
从图3中我们可知道阴影部分面积为:a2-b2.从图4中我们可知道阴影部分面积为:(a+b)·(a-b).显然两者是相等的,所以平方差公式a2-b2=(a+b)·(a-b)成立.
其实有了几何解释,中学生对于完全平方公式与平方差公式就会有一个更深刻的理解,就会使得公式的理解不仅仅停留在字母的言语信息的记忆,更重要的是公式的内涵与实质.这不禁会引起我们思考:求根公式是否也可以用几何图形表示呢?当然答案是肯定的.
下面用几何图形解释求根公式[3]:
如图5所示,正方形ABCD是由四个面积为s的全等矩形和一个面积为t2的小正方形所围成的.其中四个矩形的长和宽分别为x,y,小正方形边长为x-y.
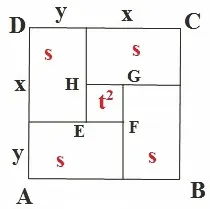
图5
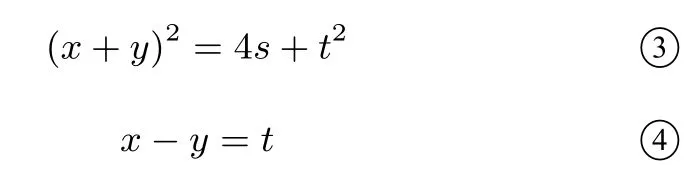
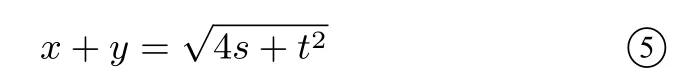
小结:一元二次方程的求根公式也可以用几何图形解释了,通过几何解释我们可以看出求根公式的又一教育价值:通过求根公式这样一个例子更有力地反驳了那些对数学有偏见的人的观点,数学不是一些枯燥无味的公式,求根公式也是可以用美丽简洁的图形来解释的,从几何解释中,我们看到了数与形之间的完美结合,体会到数形结合的思想方法.让学生不仅从懂得求根公式的表面的言语信息,还能从几何的角度深入理解求根公式.
4.求根公式的自身特征
深入理解求根公式可以让更多人对求根公式刮目相看,从此喜欢求根公式.对于求根公式的再理解,除了推导过程、几何解释之外,求根公式自身蕴含了很多数学之美,包含了多重地教育价值:
(1)从未知数与系数的角度看,求根公式告诉我们,二次方程的实根由其三个系数完全确定,至于未知数用什么字母(x,y,z,t,s,···)表示没有关系,同样,未知数所代表地实际意义(时间、路程、速度、边长等)也是没有关系的.这是一个“万能公式”,它向我们展示了数学的抽象性、一般性和简洁美.
(2)从运算地角度看,公式包括了初中阶段学过的全部六种代数运算:加、减、乘、除、乘方、开方.其中除法要求分母不为零,这是满足的;开平方要求被开方数非负却并非总能满足,因此有的方程有实数根,有的方程没有实数根.能够包含六种代数运算体现了公式的统一性与和谐美.
(3)从方程的观点来看,当公式中三个量为常数时,则它是关于第四个量的方程,比如当a,b,c为确定的数值时,它便是关于自变量x的方程,当a,b,c,x中不只有一个变量时,若视其中一个字母为变量时,其余为常数,则它是关于这个变量的一元方程;若视其中两个字母为变量,其余为常数,则它是关于这两个变量的二元方程.
(4)从解题的顺序看,求根公式将抽象的解题思想(降次地思想-通过配方、开方来实现)转化为具体的解题操作,思想不再是空洞的,操作也不再是盲目的了,求根公式中各级运算地顺序决定了一元二次方程用公式法求根地解题顺序:
(5)从整体上看,公式本身回答了解二次方程的全部三个问题:
5.对求根公式的几点教学建议
绝大多数初中教师对于求根公式的教学仅仅停留在公式的表面理解、死板地记忆与机械式地运用,根本没有多花一点时间让学生多了解一点求根公式的魅力,所以导致很多学生不喜欢求根公式,难以理解与记忆公式.因此,本文就这现象对求根公式的教学提出了以下几点建议:
[1]章建跃.义务教育教科书(数学九年级上册)[M].北京:人民教育出社,2013.
[2]刘玉波.一元二次方程求根公式的推导及教育价值[J].福建中学数学,2013(03):30-31.
[3]卢子文.平方带纵与古算诗题的一元二次方程[J].中学数学杂志,2010(02).
[4]罗增儒.数学的领悟[M].河南:河南科学技术出版社,1997.
[5]夏星.数学公式教学的几点建议及其示例[J].课堂教学研究,2008(06).

