串联数学问题,拓展学生思维

广东省恩平市年乐夫人学校(529400) 陈素屏

串联数学问题,拓展学生思维

广东省恩平市年乐夫人学校(529400) 陈素屏

问题是数学产生、起源与发展的动力.教材在概念、公式、性质和定理的教学中到处可见运用数学问题开展教学的范例.教师在教学中串联数学问题,有利于激发学生探索数学知识的发展,领悟数学知识的联系,启发学生钻研更深刻的数学问题,从而使学生深层次参与教学过程,为学生可持续发展打下良好的基础.教师串联数学问题进行教学时,必须要以学生为主体,以学生互动为主线,其教学过程大致如下：

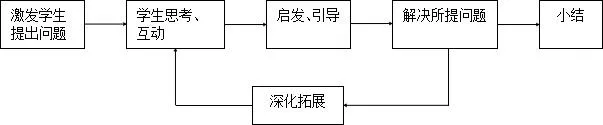
图1

一、串联数学问题

1.利用知识的发生过程串联问题,加深知识.

教材由于篇幅所限,知识的发生过程时有所略,教师在提出问题时就要发挥“主导”作用.这时可根据知识的发生过程来串联问题,将数学问题拓展,以利学生在掌握知识发生过程中,培养学生解题能力,深化数学思维品质.如在《一元一次不等式组》的教学可以这样设计：

串联方案一：具有一般性,可用于新课授课.

问题(三)题中的大括号表示什么意思?

问题(四)请用式子表达这个不等式的解集.

通过上述问题设计,层层拓展,不但使学生学会解不等式组,而且使学生明确解不等式的目的以及确立了如何构建不等式组的方法.

串联方案二：根据知识网络串联问题,拓展知识,可用于复习提高课

串联数学问题目的不仅是教会学生解某一条题,更重要的是教会学生将知识有机地结合起来,构建知识网络,形成能力.承接上面提出的问题,我们可以进一步利用问题将知识拓展.

问题(一)不等式2x+2＜0和3x-6＞0有公共部分吗?(空集)

问题(三)求不等式(2x-2)(3x-6)＞ 0,与不等式的解集可转化为问题(二)求解吗?问题(四)当不等式组中不等式的个数为三个时,解题方法怎样?由n个不等式组成的不等式组呢?解题方法又怎样?

上述问题的设计揭示了由二个不等式组推广到n个不等式的求解,由二个不等式组求解,运用到高次不等式和分式不等式的求解.帮助学生构建了知识网络.

串联方案三：体现知识的联系,适用于尖子辅导教学

问题(五)：通过“等号”与“不等号”的改动,你有什么体会的“规律总结”?

这些数学问题串联,体现了逆向思维,“等”与“不等”关系的转换,为今后学习数学打下良好的基础.

2.根据数学的思想方法串联问题,拓展知识

例如以平移、旋转的基本变换进行图形变换,培养学生的运动变化的数学思想,下面我们先看在《全等三角形》一章中,教材怎样利用几何变换的思想串联问题,让学生构建知识体系：

例1、已知：如图2,AC=AD,∠CAB=∠DAB求证：△ACB ∼= △ADB

例 2、已知：如图 3,AD//BC,AD=CB求证：△ADC△CBA

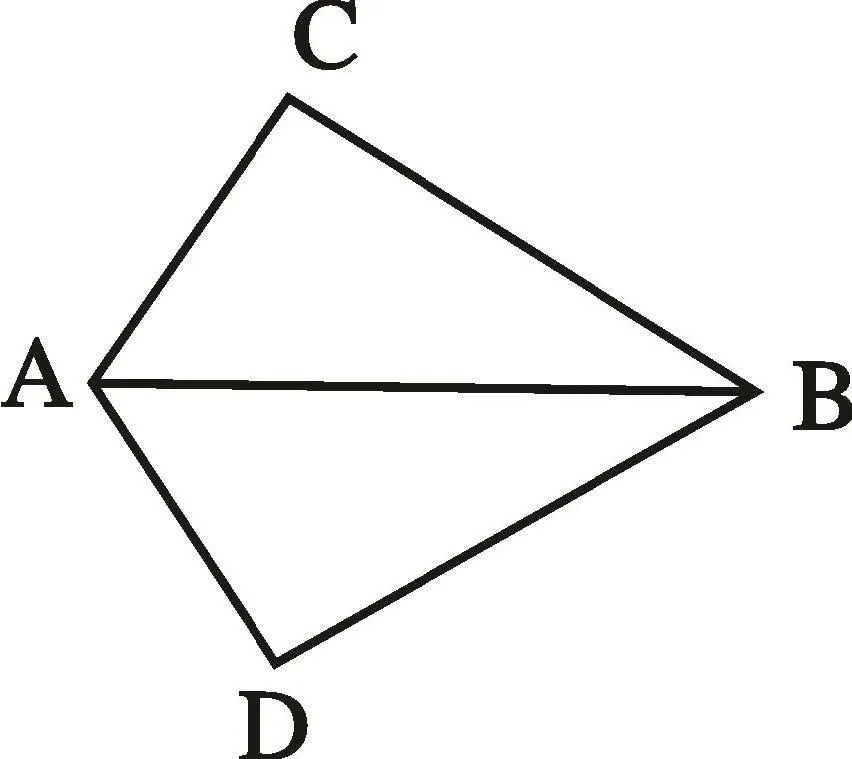
图2

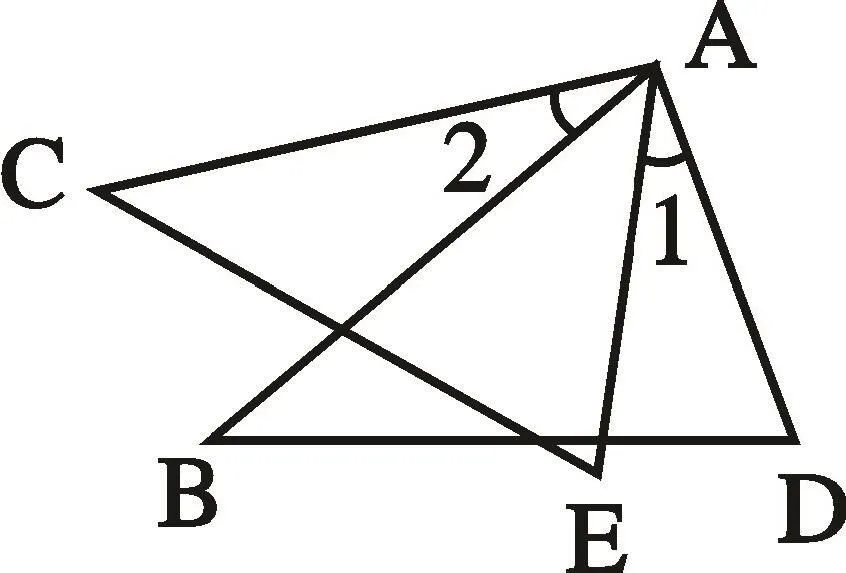
图3

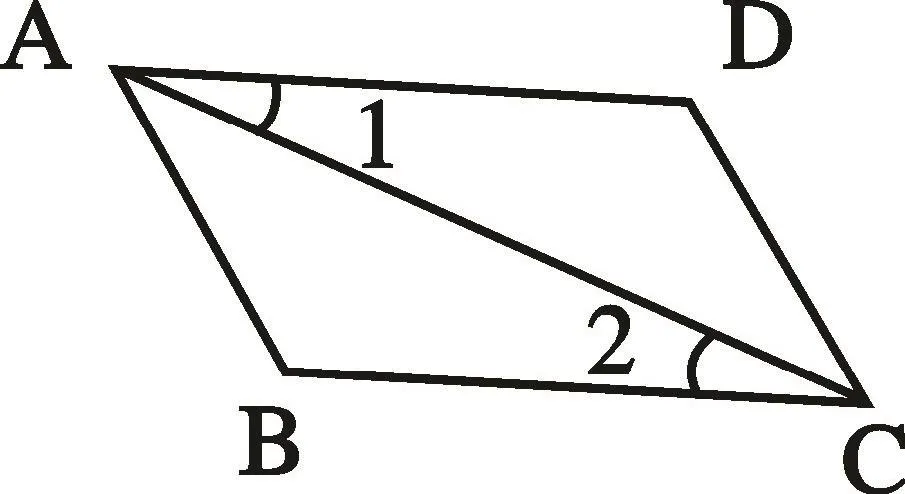
图4

例3、已知：如图4,AB=AC,AD=AE,∠1=∠2求证：△ABD△ACE

可借助以下两个全等三角形的平移、旋转这些最基本图形变化方法让学生明确三角形全等变换中图形的形状、大小、位置关系的变化,帮助学生建立图形全等变换的数学思想,运用平移,全等变换思想提高学生的解题能力.例题变换方式：

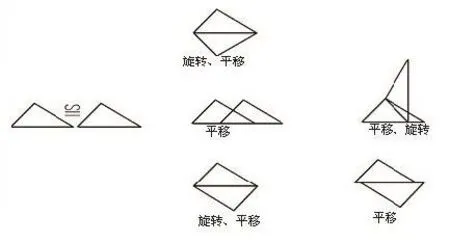
图5

二、拓展数学问题

1.拓展数学问题的作用

怎样拓展数学问题是教师在课堂中体现和实施启发式教学的重要手段.通过将数学问题拓展揭示数学知识和蕴涵数学知识中的数学思想方法是教学过程的重要组成部分.恰当地拓展数学问题有利于突破知识难点,突出重点.有利于及时反馈教学信息,掌握学生的学习动态,调整教学进程.有利于培养学生的发散思维能力和创造力.我们明白问题拓展的作用,才能在教学过程中精心设计好的问题.

2.拓展数学问题的方式

数学教材主要包括数学概念的确立,定理的推导和数学知识的运用这三种类型课题,数学思想和技能渗透其中.而拓展数学问题的方向恰好是教师通过数学问题设计,揭示概念的内涵和外延,引导学生探究知识,以及强化学生对知识运用的表现形式.教师要注重数学问题拓展的方式,努力串联好的数学问题.

方式一：串联数学问题链,层层推进,纵向拓展.

例如：证明“四边形内角和等于360°”这一定理时,我串联了如下一条问题链：

(这里学生会有很多种转化方式,教师要注意巡堂和指导,同时每种转化方法,可能会遇到不同的问题,我是选择了其中两种转化方法,继续设计问题的)

如图6、7

图6

图7

学生在解决上述问题时,既巩固了旧知识,又学到了新知识,而且在解决问题的过程中学会了图形的分割方法,转化思想,还从这些问题出发,探究了多边形内角和,激发了学生的学习兴趣,培养了学生的探究精神,真正让学生得到了自主的发展,体现教学以人为本.

方式二：串联数学问题群,横向拓展,形成网络.

我们在一章节(或一类型)的知识授课完毕后,往往要根据知识体系的脉络,对错综复杂的知识进行横向、纵向的联系,从而让学生对所学知识进行归纳,类比,形成自己的认知结构.他们对知识的结构越清晰、越稳定,对知识的运用就会越得心应手,也就越能诱发他们的创新意识.

例如,在研究二次函数的图像和性质一节中,我设计了这样一些问题,帮助学生构建知识网络(部分).

三、几点体会

1．串联题材丰富,内容深刻,情景新颖的数学问题,不仅可以激发学生的学习兴趣,更重要的是能使学生在运用数学基础知识解决数学问题的过程中,优化了思维品质,培养了研究、开拓的创新精神,为今后继续学习一切知识打下良好的思维基础.

2．要串联好的数学问题,教师必须要深入钻研教材,把握教材,了解教材的内在联系,才能深入浅出,有的放矢地根据实际提出有效的数学问题.

3．教师不仅数学知识要广阔,要了解些数学发展史、科学知识、人文知识和社会实践,也要有较好的修养,这样才会串联有趣味,有价值的数学问题.至于串联的数学问题是否有深刻性和较高的数学价值,那就更取决于教师的素质和修养.

[1]杜宪刚.拓宽引导途径,发展提问能力[J].中学数学教学参考,2009(9)：24-26

[2]王先进.一节用问题串来驱动的复习课[J].中学数学教学参考,2011(7)：22-24