借题发挥促进学生发展数学核心素养
广东省中山市坦洲实验中学(528467) 高艳玲
借题发挥促进学生发展数学核心素养
广东省中山市坦洲实验中学(528467) 高艳玲
发展学生数学核心素养是数学课堂教学的基本任务.为了帮助学生发展数学核心素养,教师必须要解决好三个问题:一是如何选择最优问题,使每个题目具有典型性、代表性和示范性,避免题海战术;二是如何借题发挥,使问题解决达到“解一题通一类,做一题知一法”的举一反三效果;三是如何最大限度地挖掘题目蕴含的数学方法、解题规律,达到训练学生的数学思维的目的.其中,最关键最核心的问题是借题发挥,促进学生发展数学核心素养.笔者结合个人多年的初中数学教学经验,尝试从以下四个方面来谈一谈如何借题发挥促进学生发展数学核心素养.
一、多角度串联问题,发展学生数学抽象素养
发展学生数学抽象素养的比较好的方法是引导学生寻找题目与题目之间规律的同一性、思维的相似性、方法的关联性.因此,教师在教学设计时要有意识地将类似问题串联.串联可以是纵向梯度串联,即同一知识点的层层深化;也可以是横向平行串联,即同一知识点的角度变化.教学实践中只有善于从杂乱无章的题目中,概括出一般规律和方法,学生才在经验迁移和触类旁通中实现数学抽象.
案例一:如图1,△ABD和△AEC分别是以△ABC的边AB和AC为边长的等边三角形,求证:BE=DC.
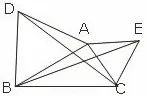
图1
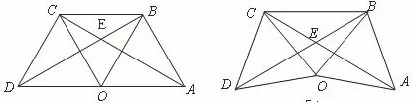
图2
变式一:如图2,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边△OAB和等边△OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;
变式二: 如图3,若将上述条件中的三角形改为四边形ABCD和四边形DGFE分别是以△CDE的边CD和DE为边长的正方形,求证:AE=GC.
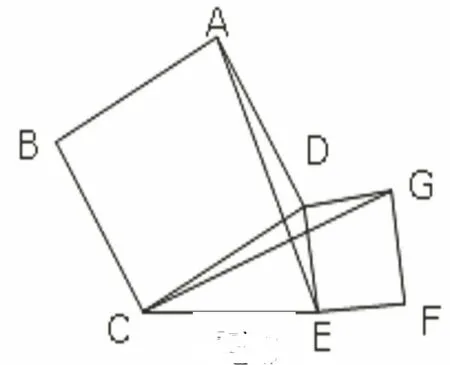
图3
两道变式题,虽然呈现形式和几何背景发生了变化,但是问题的实质却没有发生变化,仍然是利用正多边形提供的边、角相等条件导致三角形全等.这样设置问题便于让学生透过现象看到问题的本质,有利于培养学生思维的深刻性.引导学生进行分类对比,多题归一,找到解决同一类题的规律和方法,从而达到举一反三实现数学抽象的目的.
二、多层次激活“母题”,发展学生逻辑推理素养
数学“母题”具有代表性、典型性、示范性、统领性,能够体现出数学基本方法和规律,如果把一类题比喻成一颗大树,那么母题就是树根,千枝万叶源于树根,所以引导学生抓住了“母题”,也就抓住了问题的关键,可以达到一题多用、触类旁通、事半功倍之效,而且能有效地帮助学生发展数学逻辑推理素养.
案例二:如图4,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,求证:阴影部分四边形OFCG的面积是△ABC面积的三分之一.
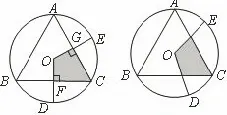
图4
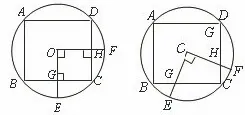
图5
变式一:如图5,正方形ABCD内接于⊙O,OE、OF为⊙O的半径,OE⊥BC于点G,OF⊥CD于点H.求证:四边形OHCG的面积是正方形ABCD的面积的四分之一.
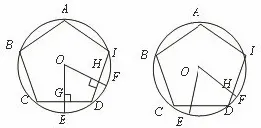
图6
变式二:如图6,正五边形ABCDI内接于⊙O,OE、OF为⊙O的半径,OE⊥CD于点 G,OF⊥ID于点H.求证:四边形OHDG的面积是正五边形ABCDI的面积的五分之一.
……
变式三:如果是正n边形A1A2···An内接于⊙O,情况又如何?
处理好一些特殊几何图形的数量关系的“母版”,其他图形就是它的变式.对于母题及其变式问题的解决与比较的过程,就是发展学生逻辑推理素养的过程.教学实践中要紧扣教材,夯实基础,同时对典型问题进行变式引导,做到以不变应万变,提升迁移能力,发展逻辑推理素养.
三、探索图形规律,发展学生直观想象素养
几何图形进行图形变换,往往呈现一定的规律,引导学生探索图形变换蕴含的规律,不仅有助于学生对几何图形的认识,对几何图形性质的认知,对几何图形变换的感知,对几何图形中相关元素关系的感悟,对几何图形整体的想象,而且有助于学生通过规律探索的过程发展直观想象的素养.
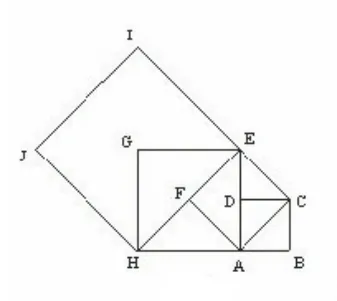
图7
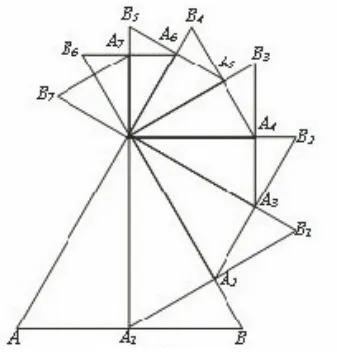
图8
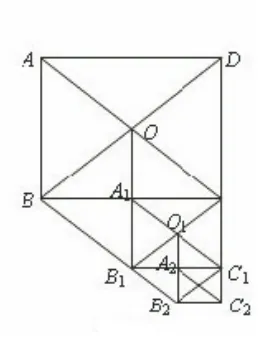
图9
案例三:如图7,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去……
(1)记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,···,an,请求出a2,a3,a4的值;
(2)根据以上规律写出an的表达式.
变式一:如图8,已知等边△OAB的边长为a,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2.
(1)求线段OA2的长;
(2)若再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,···,△OAnBn.求 △OA6B6的周长.
变式二:如图9所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1···依次类推.
(1)求矩形ABCD的面积;
(2)求第1个平行四边形OBB1C、第2个平行四边形A1B1C1C和第6个平行四边形的面积.
这组题图形呈现方式比较新颖,几何背景虽然比较复杂,但学生只要通过研究图形的产生过程,就不难发现规律:正多边型及特殊四边形中相关线段与边长之间的关系.属于同一题型的多种变化,但是万变不离其宗.教师要引导学生发现这些变化,并能发现解决此类问题的一般方法,从而发展学生直观想象素养.
四、深层次挖掘考题,全面发展学生数学核心素养
引导学生解题时,既要提倡以求同思维为基础的“通法”,又要注重以求异思维为突破的“优法”.“通法”可以至熟,“优法”可以生巧.过份强调“通法”,会导致学生解题思维的僵化,不利于思维的灵活性的培养.故解题时要在“通法”的基础上加强“优法”的引导,通过一题多解,让学生“学有所悟”.从中比较孰繁孰简,孰优孰劣,久而久之,能够精益求精,突破常规.这类探索活动,有利于学生全面发展数学核心素养.案例四:已知:AB是⊙O的弦,半径OC,OD分别交AB于点E,F,且AE=BF,证明:OE=OF.
证法一:连结OA,OB然后证明△AOE∼=△BOF(证法略)
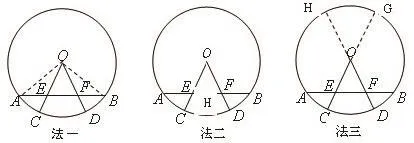
图10

以上三种证明方法,利用了垂径定理、全等、相交弦定理等多方面的知识,学生通过不同的方法在同一问题情境中正确应用,加深了对基础知识的理解,发展了学生多维度、多层次、多角度地分析解决问题的能力,增强了学生思考问题的广度、深度和精度,培养了学生思维的发散性、灵活性和开放性,有利于学生全面发展数学核心素养.
总之,通过“借题发挥”可以大大提高学生学习的效率,促进学生基本活动经验的积累,发展学生数学核心素养.
[1]任勇:你能成为最好的数学教师[M]上海:华东师范大学出版社,2010.11
[2]顾明远:把学习的选择权还给学生[J].河北师范大学学报(教育科学版),2012,(1):5-7

