基于玲珑画板技术的数学实验设计探索

广东省珠海市斗门区第一中学(519100) 唐学宁

基于玲珑画板技术的数学实验设计探索

广东省珠海市斗门区第一中学(519100) 唐学宁

当下信息技术迅猛发展,数学教学中融入技术已成为时代的需要,各种数学教育技术软件及平台也逐步进入中学数学课堂,教学中,如何设计数学实验、如何利用数学实验提升学生学习数学的兴趣以及提高学生的数学成绩,已成为数学技术整合到高中数学的重要话题.笔者参考已有的一些数学实验设计,结合教学中利用玲珑画板软件实践经验,撰写此文,抛砖引玉,希望有更多同仁参与到数学实验的设计中来.

一、数学实验设计应注重趣味性

“知之者不如好之者,好之者不如乐之者”,兴趣是最好的老师.在数学实验的设计过程中,如果我们适时地增加一些提升学生兴趣的内容,能让复杂抽象的认识活动变得简单而直观,促使学生积极主动地参与学习.

案例1.函数称之为囧函数,请大家利用软件画出图像并指出函数的单调区间.

分析：针对函数单调区间的认识,常见的设计方法是由PPT给出一个函数图像(如图1),然后由学生观察图像,并说出单调区间.此方法可以让学生形象的观察出函数的上升与下降趋势,并依此指出函数的单调区间.

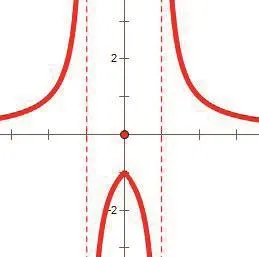
图1

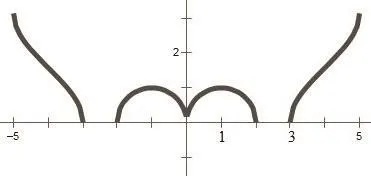
图2

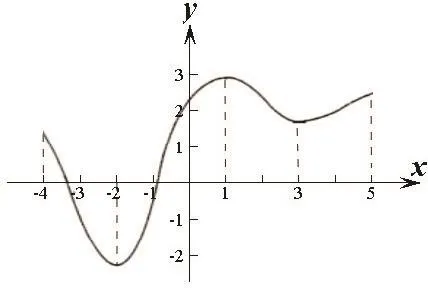
图3

设计：实际教学中,笔者给出案例1,要求学生利用玲珑画板的画函数图像功能自行输入函数解析式画函数图像.学生画图像时,开始没有考虑定义域,结果作出的图像上顶天下不着地.经过思考,画出函数图像如图2所示,很像一个中文的囧字,顿时个个都露出会心的微笑,之后再让学生指出函数的单调区间,轻松至极.趁此机会,笔者提醒学生,课后还可以自己搜寻一些特殊的函数并画出图像.图3正是学生探索后发现的一个函数图像,学生们称它为：眼镜函数.

整个教学过程中,让学生领会了除列表、描点、画图的函数图像画法之外,还可以使用画板软件画函数图像,开阔了学生的眼界,让他们的思维插上了翅膀,得以在数学的函数世界翱翔.

二、数学实验设计应注重形象性

空间想象能力是对空间图像的观察、分析、抽象的能力,要求学生能根据条件作出正确的图像,或根据图像想象出直观形象;能正确地分析出图像中基本元素及其相互关系;能对图像进行分解、组合;会运用图像与图表等手段形象地揭示问题的本质.

在数学实验的设计中,要是我们能够把要求学生必须要想象的问题形象化,然后再由学生模仿、联想,一定会收到不错的效果.

案例2.某几何体的三视图如图4所示,其俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是___.

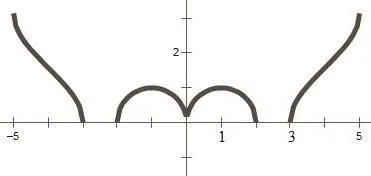
图2

分析：对于三视图问题,常见的方法是要求学生发挥想象力,然后在草稿上画出直观图;平时学生只是在教室学习,缺少直接观察的模型,要想在考试的短短时间画出直观图,难度较大.

设计：实际教学中,笔者采用玲珑画板首先画出三视图,然后利用精确旋转命令把左视图与俯视图旋转成如图5所示的形状,再利用对齐命令把左视图

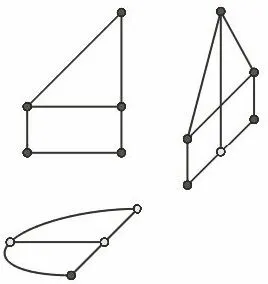
图5

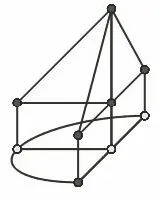
图6

与正视图对齐成图6所示形状,最后利用复制工具把图形还原成直观图(图6),很自然的发现图形是由一个半圆锥与一个半圆柱构成.

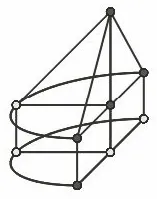
图7

在这个过程中,学生目之所见是图形的动态旋转,耳之所闻是教师精细的步骤讲解,不知不觉中就学会了还原法画三视图直观图的方法：首先旋转左视图与俯视图,然后把正视图与左视图对齐到俯视图上,最后添加必要的线段构成直观图.

三、数学实验设计应注重探究性

善于发现知识间联系并用于解决新问题,是数学创造性思维活动的重要特征.在数学实验设计过程中,教师如果有意识地选择一些具有挑战性的探究问题,为学生创造自主探究与发现的机会,将会很好的培养学生的创新意识与创造性思维能力.

案例3.人教A版教材选修2-1《椭圆》一节中设计了“探究与发现”：用一个平面去截圆锥得到的截口曲线为什么是椭圆?

图8

图9

分析：对于平面截圆锥的问题,教师常常因为高考中根本不会考查,从而要求学生自己阅读,或者采用拿个模型到班给学生一看了之.殊不知,教材设置这个内容,必定是经过千锤百炼,有它自己特定的作用：理解椭圆的几何特征.

设计：实际教学中,笔者使用玲珑画板软件,制作了平面截圆锥得到圆(如图8),得到椭圆(图9),以及得到双曲线与抛物线的动画,并让学生总结出：当平面与圆锥母线平行时得到抛物线,当平面与圆锥底面平行时得到圆,当平面与母线不平行时,得到椭圆或双曲线一支.学生感觉很新奇,纷纷要求继续给出证明.

如图10,在圆锥内的截面两侧各放置一个球,使上下两球都与截面、圆锥侧面相切,记球与截面的切点分别为F1,F2,球与圆锥侧面的交线分别为圆O1,O2,在截口曲线上任取一点P,作过点P的圆锥母线,与圆O1,O2分别交于M、N 两点,因为PF1,PM都是圆O1的切线,故PF1=PM,同理可得是定值,易知MN＞F1F2,因此P点的轨迹为椭圆.

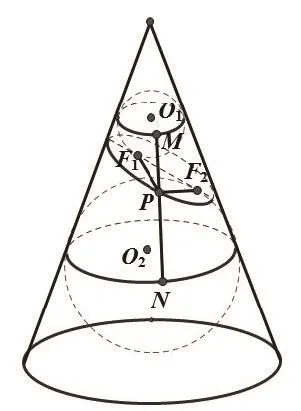
图10

在本案例的解决过程中,不仅让学生形象的看到了平面截圆锥得到的几种曲线,而且让学生领会到圆、球、圆锥与椭圆等几何图形之间浑然一体的联系.

四、数学实验设计应注重应用性

近年来,高考指挥棒下,数学科俨然已丧失美的教育,逼迫学生成为做题的机器,更有甚者,有调查显示,七成网友要求数学滚出高考,这是我们数学人的悲哀.作为一线数学教师,我们要不断的去挖掘数学在生活实际中的点滴应用,积极的去传授数学的在生活中的应用,让学生感受到数学的独特美.

案例4.德克萨斯扑克全称Texas Hold’em poker,中文简称德州扑克,它是一种玩家对玩家的公共牌类游戏一张台面一般由2-10人参加,德州扑克一共有52张牌,没有王牌;牌型中“皇家同花顺”是指：由AKQJ10五张组成,并且这5张牌花色相同,“四条”是指：4张同点值的牌加上一张其他任何牌,平时我们都认为四条(炸弹)非常大,请问为什么在德州扑克里“皇家同花顺”比“四条”大?

分析：要弄清楚为什么皇家同花顺比四条大,其实只需要研究皇家同花顺出现的概率与四条出现的概率,哪个出现的概率小,就应该哪个大;如果学生研究52张牌随机派发5张,出现皇家同花顺的次数与出现四条的次数,然后比较大小也一样可行.

设计：实际教学中,笔者使用玲珑画板软件,制作了简单的扑克派发程序,然后要求学生计算皇家同花顺出现的概率：再计算四条出现的次数,第一步先从13套牌中选一套有种,然后再从剩下的48张牌中选一张有方法,因此出现四条的概率为由此可见,四条出现的概率虽然也比较小,但是却是皇家同花顺出现概率的156倍,可见皇家同花顺比四条大一点都不出奇了.

在计算完皇家同花顺与四条之后,我更进一步要求学生计算出现“葫芦”(三对二)、“同花”(5张牌花色相同,但是不成顺子),“3条”(三张牌点值相同,其他两张各异)等牌型的概率,学生兴味盎然,又开心,又积极,感觉不仅学到了知识,还能应用于实际.

综上所述,数学实验的设计是以现行教材上的数学内容的某个知识点或者学生在数学学习中遇到的问题为研究对象,设计成供师生共同实验学习的问题.在实验过程中,学生通过自主探究,合作交流,在研究中学习,在学习中研究.在技术应用的过程中,不能停留在玲珑画板的功能应用,而是应该整合玲珑技术的优势,反复锤炼我们数学的精品实验,力争提高学生解决实际问题的能力.

[1]余明芳王钦敏.例谈数学探究课题的选择与教学设计[J].高中数学教与学,2016(5)：29-32.

[2]徐章韬.用信息技术深度挖掘课程内容[J].高中数学教与学,2016(2)：7-11.

[3]崔永红.信息技术平台下改进数学教学设计的研究[J].高中数学教与学,2016(2)：16-19.