基于数据分析下的初中数学复习课教学探索与反思*—以《与圆有关的位置关系》复习课为例

广东省广州市培正中学(510080) 汤俭

广东省广州市越秀区教师进修学校(510080) 吴平生

基于数据分析下的初中数学复习课教学探索与反思*—以《与圆有关的位置关系》复习课为例

广东省广州市培正中学(510080) 汤俭

广东省广州市越秀区教师进修学校(510080) 吴平生

随着大数据时代的到来,数据分析正影响着传统教学．如何借助数据分析的方法和手段,精准地找到学生学习的困难,为学生的课前、课中、课后的学习提供有效的服务,是笔者一直在思考的问题．在复习课中,以数据分析得到的反馈情况作为复习的起点,以学生的最近发展区来实施复习教学,以数据反馈来促进教学方式与学习方式的转变,是一种有益的尝试．基于以上设想,笔者以《与圆有关的位置关系》复习课为例开展数据分析下的初中数学复习课例研究．

一、基于数据分析下的《与圆有关的位置关系》复习课构想

为了将数据分析应用于初中数学复习课教学,在课前,我尝试用数据统计学生学习状况,确定适合学生实际情况的复习目标．在课中,我尝试通过数据统计对比,找出前后测出现的知识缺陷,有针对性地点评,找出共性问题,设置变式拓展问题．在课后,我尝试根据前后测形成的错题本,推送分层作业,为学生的“再次学习”创造条件．

本节复习课流程图如下：(前后测内容参见附录1与附录2)

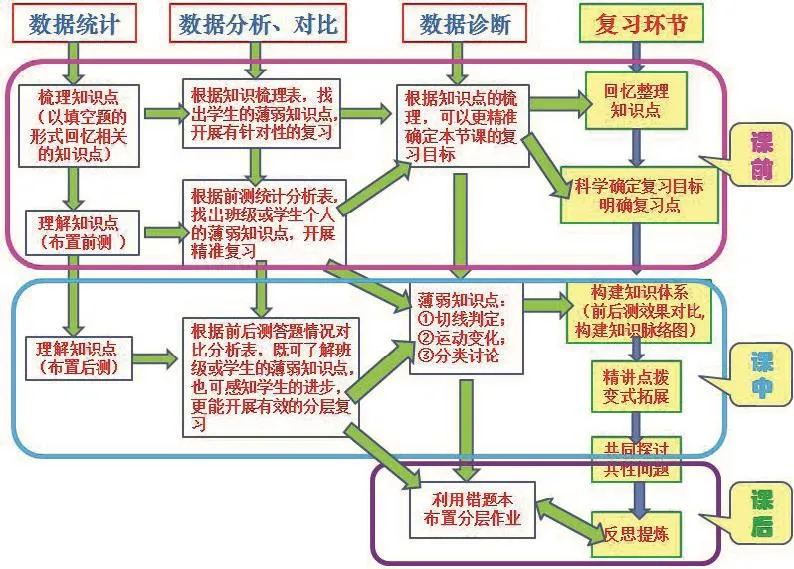
图1

【说明】在本节复习课的课前、课中和课后,学生所做的练习都是利用神算子数学网站同步布置,课中使用的数据都是基于神算子数学网站的统计分析功能而进行的．在本节复习课中,学生带手机或者IPAD等电子产品通过登录神算子数学网站完成后测,课后也是利用神算子数学网站推送分层作业．

二、基于数据分析下的《与圆有关的位置关系》复习课实践

(一)内容分析

本节复习课是以2014年人教版九上数学教材第24章《圆》第2节作为教学内容．本单元中,圆的有关概念、性质和定理比较多,图形变化也比较丰富,直线与圆的位置关系是核心内容,圆的切线的判定定理、性质定理和切线长定理是重点内容,本节内容蕴含了丰富的数形结合思想、转化化归思想等．

(二)学情分析

笔者所教班学生对本单元的基础知识掌握得较好,但容易混淆圆的切线的判定与性质中的条件与结论,综合应用能力不强．通过作业的反馈,笔者发现学生的分析问题和解决问题的能力有待提高．

(三)教学目标

1.复习目标：

2.复习重点：圆的切线的判定和性质的综合运用．

3.复习难点：用运动变化的观点和数形结合的思想方法分析直线与圆的位置关系．

(四)教学实施

1.以题带点,触类旁通——基于数据分析下的学情分析与诊断

(1)设计前测与后测内容

为了准确把握学生的复习基础,我根据平时的课堂反馈和作业批改情况整理了前测内容,并提前一天在神算子网站布置．上课前一天晚上我获得前测内容的反馈数据,并在前测内容的基础上设计了后测内容．上课时,我根据前测数据对前测内容进行了讲评．并让学生在当天课堂上完成后测内容．

(2)实验班各类数据分析

【前后测及格人数对比表1】

图2

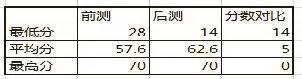
图3

【前后测各分数段对比表2】

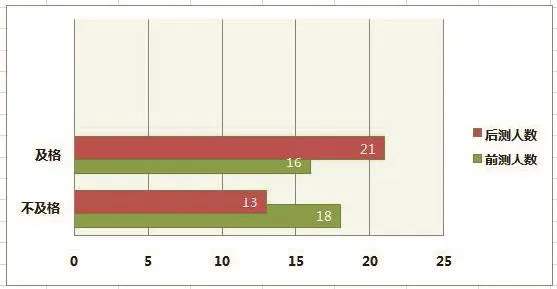
图4

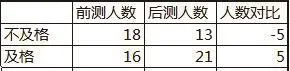
图5

【说明】通过条形图,我们发现学生的前后测发生了可喜的变化,及格人数明显增加,平均分有显著提高．

【前后测每小题得分率对比表3】

图6

【说明】前后测的题目涉及的知识点基本一致,只是在题目的表现形式上、图形的变化上、能力的要求上有所提高．通过统计表可以发现,整体正确率有了一定提高,后测第4小题的得分率达到100%．在讲评了前测第5小题的基础上,我欣喜地看到学生做后测第5小题的得分率有了很大的提高．但是后测第1小题,考查直线与圆的位置关系,由于点的位置不确定,需要分类讨论,不少学生漏解,另外由于本小题有两个空,有些学生只做对第一空,做错第二空,系统判错,导致得分率降低．第3小题的正确率也由100%下降到88.2%．通过数据的对比,我们可以及时发现自己的教学效果和学生的掌握情况,为更好地开展下一环节教学提供科学的依据．

2.以变促能,举一反三——基于数据分析下的变式教学与拓展探究

(1)梳理框图,提炼重点

帮助学生梳理本单元的知识框图,建立知识间的内在联系,使知识结构化、系统化,是本节复习课的基本目标之一．为此,我与学生一起找出本单元的知识脉络和研究方法．

图7

知识脉络：点与圆——直线与圆——三角形与圆．

研究方法：比较d与r的大小．

圆的切线的判别方法：定义法;距离法：无交点,作垂直,证半径;判定定理法：有交点,连半径,证垂直．

蕴含的数学思想：数形结合,分类讨论,转化化归．

(2)变式训练,促进迁移

根据课前的诊断数据,我发现学生对圆的切线的判断方法的理解不是很到位,为此给出了以下变式．

原题：如图8,在 △ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E．证明：DE是⊙O的切线．

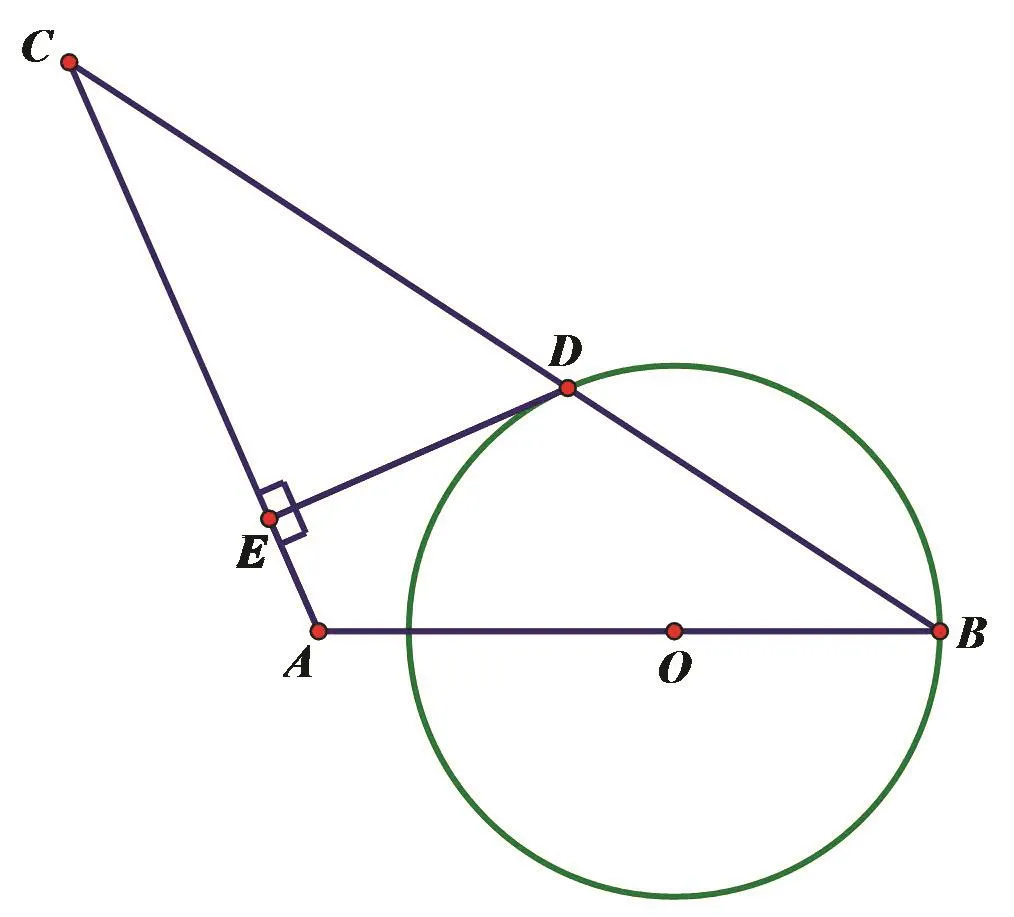
图8

【说明】本题采用小组讨论的形式,通过学生之间的交流与讨论,一共收集到三种不同的解题方法．基本方法是连接OD,证明DE⊥OD．

变式：如图9,若点O在AB边上的位置改变了,半径为OB,但AB不是⊙O的直径,BC与⊙O相交于点D,过点D作DE⊥AC于点E．试问DE还是⊙O的切线吗?为什么?

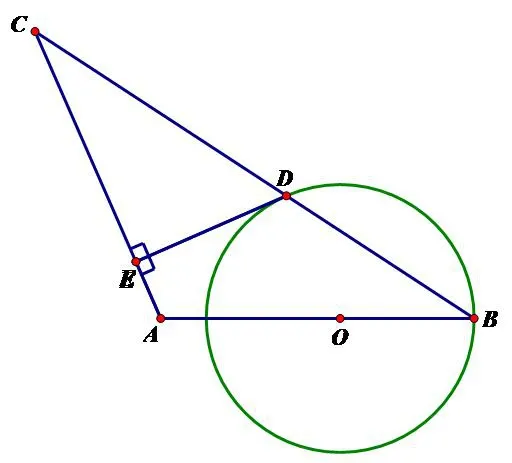
图9

【说明】通过几何画板的演示,发现DE仍是⊙O的切线．证明方法不变,还是连接OD,证明DE⊥OD．通过变式练习,让学生感受到虽然圆心的位置、圆的半径发生变化,但直线与圆相切的位置关系不变,证明圆的切线的方法也没变,从而与学生一起归纳出证明圆的切线的两种常见方法：连半径,证垂直;作垂直,证半径．让学生领悟“动中求静,变中求定”是解决运动变化问题的基本思路,为下一环节作好铺垫．

(3)例题分析,引申拓展

根据课前的诊断数据,我发现学生的运动变化和分类讨论意识较弱,因此我设置了一道有关运动变化的例题,以加强学生的运动变化意识．

图10

(I)在移动过程中,⊙O与△ABC的三条边相切几次?

(II)当t为何值时,⊙O与AC相切?

【说明】用几何画板动画演示,解题过程略．

3.以错促思,提升自我——基于数据分析下的师生课堂生成

(1)动态课堂,精彩纷呈

在传统教学中,我们主要通过举手或者教师巡堂的方式来获取学生课堂的反馈信息,有些片面和模糊．但利用数据分析,可以精准统计出学生的正确率,记录下学生的做题痕迹,自动分类出学生的典型错误,实时进行教学上的调整．比如在发现第1小题的得分率下降后,我利用了网站中的数据分析功能,在出现典型错误的学生中随机抽取一位学生(这时学生的错题本也相应形成),根据她的做题情况,请学生说出自己的分析过程和出错的原因,请大家一起来纠错和改正,并顺势提炼本题的核心知识点．在师生互动纠错的过程中,学生的情绪被我充分调动起来,这时我发现第5小题的得分率显著提高,就请学生做小老师,这时有一个学生举手提出问题：“若把线段变成直线,情况如何?”我便顺势把“线段BP”改成“直线BP”让学生讨论,拓展了学生思维．

(2)建立错题本,推送分层作业

传统的作业都是老师预先准备好,教师通过统一的作业来检验学生的学习情况．但在数据分析下,教师可结合前后测的数据反馈和学生课堂做题情况从试题库推送分层作业,不同类型的学生会收到适合自己的作业．若有错题,题目会自动进入学生的错题本中,学生一方面可以通过网络随时随地进行错题反馈,另一方面可以利用数据统计的功能了解自己的掌握情况和在班上的学习排名,这样每一个学生都在适合自己的作业中取得成功,获得轻松、愉悦、满足的学习体验．

三、教后思考

1.运用数据分析可以提高复习课的教学效率与效果

在本节课例研究中,我选择了一个班是传统教学,另一个班是实验教学．通过两个班的数据统计发现,实验班的课堂教学效果比常规班好一些．相比之下,实验班的学生反馈数据由计算机同步自动完成,获得的是实时精确数据,让教师从数据统计中解放出来,提高了教学效率．教师可以随时处理“生成”数据,精准点评,提高了教学诊断的实时性与精准性．

【实验班与常规班统计对比表】：

【对比表1】

图11

【对比表2】

图12

【对比表3】

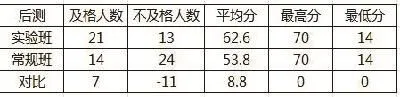
图13

【对比表4】

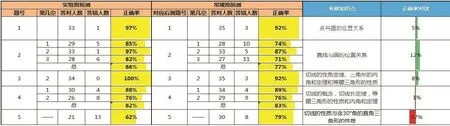
图14

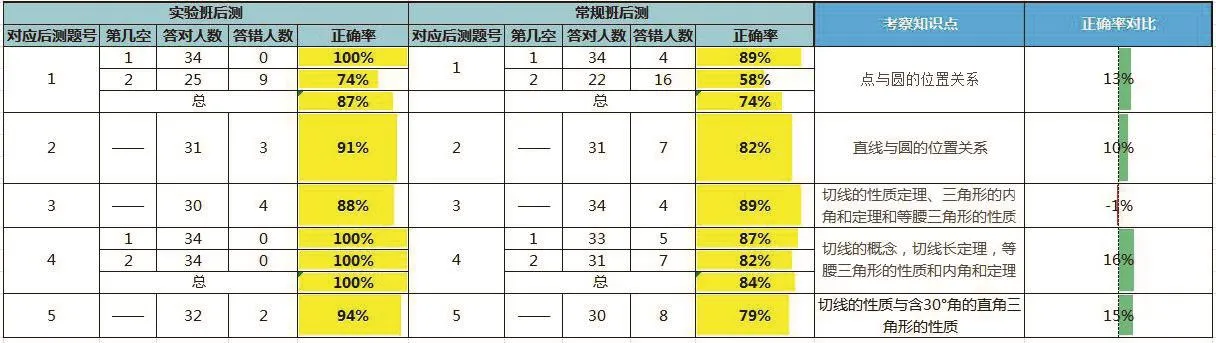
图15

【说明】前后测成绩满分均为70分,常规班的数据是由神算子网络公司利用学生的做题试卷课后完成统计分析．从实验班与常规班前后测的成绩对比可以发现：实验班的成绩进步较大,平均分由57.6分提高到了62.6分,常规班的成绩由57.8分下降到53.8分．在前测中,实验班与常规班的及格人数相差1人,但在后测中,实验班合格人数进步明显,比常规班多了7人(见对比表1与表2);在前测中,实验班的第1至4小题的得分率都比常规班高,但实验班第5小题的正确率比常规班低17%(见对比表3);在后测中,实验班每小题的表现比常规班优势更明显,优势基本在10%以上(见对比表4)．

2.基于数据分析下开展复习教学需要教师提高课堂调控能力

在本节课例研究中,我们发现教学的顺利进行离不开网络的帮助,如前后测的正确率统计,成绩分布图,满分人数统计,每个分数段的统计等．如果网络出现问题,会影响整节课的顺利开展．在本节课上,我正准备上课时网络发生了意外,连不上网,耽误了将近10分钟,严重影响了我的上课情绪和打乱了我的上课节奏．通过这个例子说明,我们借助网络来开展教学,要做好充分的思想和技术准备,师生要提前检查好网络设备,熟悉好网络功能键,安排好学生探究活动时间,突出教学重点,以便有效达成教学目标．

3.运用数据分析进行复习教学要注意“效”和“度”

基于数据分析开展复习课教学有助于教师精准了解学情,为实施分层教学提供科学依据,但一味追求数据分析的所谓“精准”,有可能出现适得其反的效果．在本节课例中,笔者根据数据分析统计出的结果,围绕学生出错的题目进行变式引申,讲在学生的薄弱点和易错处,受到学生欢迎,但感觉被题目牵着鼻子走,有就题论题之嫌,总觉得没有帮助学生揭示与领悟题目之间的联系与蕴藏的数学思想方法,只是一味告知学生,教学效果不是很满意．本节课的前后测主要反映了近迁移的学习效果,但远迁移的学习效果还有待验证．如何借助数据分析来提高复习课的效果和广度,仍需不断探索．

附录1：《与圆有关的位置关系》复习课前测内容

1.⊙O的半径为10 cm,点P到圆心的距离为8 cm,则点P在⊙O___.

(选择字母填空,A：内,B：上,C：外)

2.在 △ABC 中,∠ACB=90°,AC=3,BC=4.

(1)若以C为圆心,r=2为半径作圆,则直线AB与⊙C的位置关系是___.

(2)若以C为圆心,r=2.4为半径作圆,则直线AB与⊙C的位置关系是___.

(3)若以C为圆心,r=3为半径作圆,则直线AB与⊙C的位置关系是___.

(选择字母填空,A：相切,B：相离,C：相交)

3.如图15,AB是⊙O的直径,BC是⊙O的切线,且AB=BC,则 ∠A=___.

4.如图16,PA,PB是⊙O的切线,点A,B为切点,AC是 ⊙O 的直径,AC=6,∠CAB=30°,则 ∠P=___°,AP=___.

5.如图17,∠APB=30°,点O是射线PB上一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离是___.

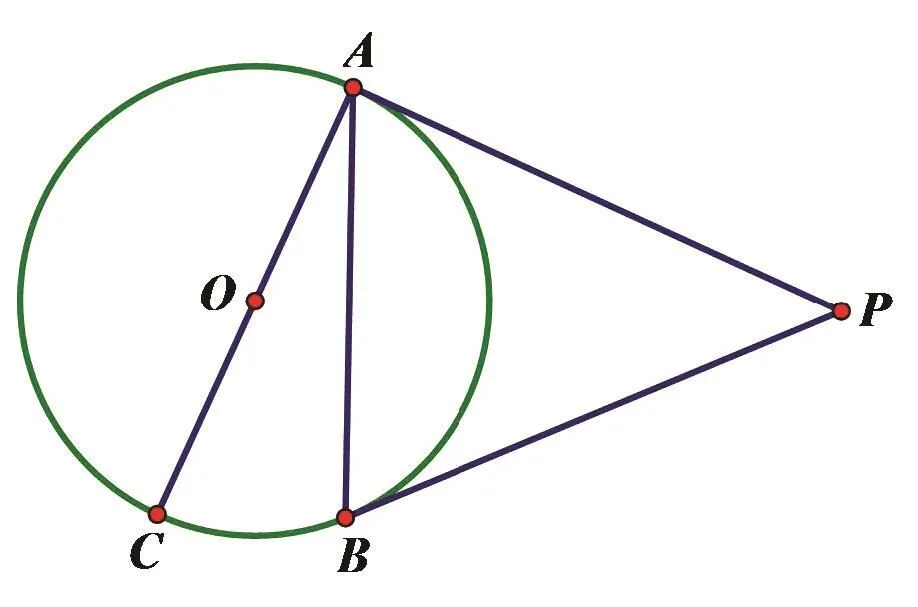
图16

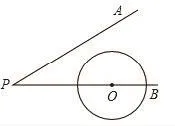
图17

图18

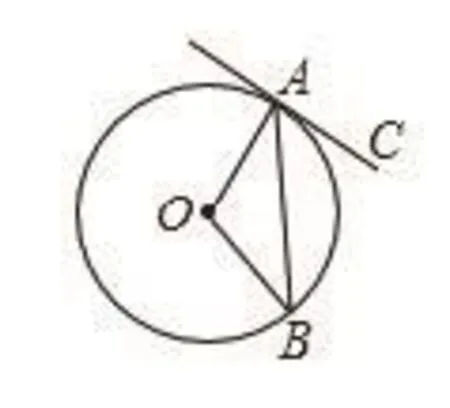
图19

附录2：《与圆有关的位置关系》复习课后测内容

1.已知⊙O的半径为5,直线l上有一点P满足PO=5,则点P与⊙O的位置关系是___,直线l与⊙O的位置关系是___.

(选择字母填空,A：在圆上,B：在圆内,C：在圆外,D：相切,E：相交,F：相切或相交)

2.已知等腰三角形ABC中,AB=AC=13cm,BC=10cm,以A为圆心,13cm为半径的圆与直线BC的位置关系是___.

(选择字母填空,A：相离,B：相交,C：相切)

图20

图21

3.如图18,CA是⊙O的切线,切点为A,点B在⊙O上,如果 ∠CAB=55°,则 ∠AOB=___°.

4.如图19,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠APB=50°,则∠PAB=___°,∠CAB=_____°.

5.如图20,∠APB=30°,点O 在PB 上,⊙O的半径为1cm,OP=6cm.若⊙O在线段BP上沿BP方向以每秒2cm的速度平移,当圆心O平移____秒时,⊙O与直线PA相切．

[1]雷明生,马红丽．浅谈数学中考第一轮复习的课堂教学模式[J]．中国数学教育(初中版),2009(4)．

[2]徐强．新课程理念下数学总复习课的设计范式和解读[J]．中国数学教育(初中版),2007(5)．

[3]温伟明．基于大数据分析下的小学数学互动课堂[J]．中国现代教育装备,2016(9)．

[4]丁永刚．借助网络进行变式教学的探究与思考[J]．中学数学教学参考 (上旬),2015(10)：16-20 ．

广东省教育科学规划课题“基于不同课型的初中数学教学策略整合研究”(课题批准号：2014YQJK018);广州市越秀区科信局课题“基于自主学习的初中数学复习课的有效学习策略研究”(课题批准号：2015-JY-009)