关于正规矩阵的注记
贾 杰,任芳国
(陕西师范大学数学与信息科学院,陕西西安710062)
关于正规矩阵的注记
贾 杰,任芳国*
(陕西师范大学数学与信息科学院,陕西西安710062)
利用正规矩阵特征值和奇异值的定义,联系谱范数、Schur引理、极分解、矩阵酉相似对正规矩阵进行了等价刻画,得到正规矩阵特征值和奇异值存在关系σi=|λi|,i=1,2,…,n,λ1,λ2,…,λn,σ1,σ2,…,σn分别为A的特征值和奇异值,正规矩阵特征值和它的迹存在关系数学分析及类比思想获得了正规矩阵唯一分解,推广并证明了正规矩阵下的内积不等式和范数不等式.
正规矩阵;特征值;迹;范数
正规矩阵是一类特殊的矩阵,是在讨论矩阵的酉等价时产生的一类矩阵,在矩阵分析中占据重要的位置.文献[1]研究了对角矩阵和正规矩阵的性质;文献[2]给出了可换矩阵的定理.文献[3]线性代数的应用给出了正规矩阵的相关性质;文献[4-8]分别研究了奇异值与特征值的内容以及正规矩阵乘积的性质等;在之后的文献中研究了特征值理论,正规矩阵定理,矩阵与算子的应用等.笔者继续研究正规矩阵的等价定理,并得到正规矩阵的奇异值是特征值的绝对值,特征值与迹的关系,正规矩阵在范数中的应用以及正规矩阵的分解及分解的唯一性.
1 预备知识
为了叙述方便,对符号约定如下:A*表示矩阵A的共轭转置矩阵,AT表示矩阵A的转置;Mm×n(F)表示数域F上的所有m×n阶矩阵的集合;Mn(F)表示数域F上的所有n×n阶矩阵的集合;tr(A)是矩阵A的迹,其中A∈Mn,其他未加说明的符号参见文献[6].
下面是与本文有关的几个定义及引理:
定义1[1]设A∈Mn,则存在n阶酉矩阵U及对角线元素为A的特征值的上三角矩阵D,使得A=UDU*,称A具有Schur分解.
定义2[2]设A=(aij)n×n∈Cn×n则||A||2=,λ1为A*A的最大特征值.
定义3[5]设A=(aij)n×n∈Cn×n,若A*A=AA*,则A正规.
定义4[6]设A∈Mn(C),则A=U|A|,其中A是A*A的平方根或A=|A*|U,称为极分解.
引理1[3]设矩阵A∈Mm×n(C),则存在两个酉矩阵V∈Mm和W∈Mn及矩阵Σ=[σij]∈Mm,n,
其中σij=0(i≠j)且σ11σ22…σqq0,其中q=min{m,n},使得A=VΣW*,其中σii,i=1,2,…,q为A的奇异值,称A具有奇异值分解.如果A是实的,那么V∈Mm和W∈Mn是实正交阵,Λ=引理2[4]设A,B,C,D都是n×n阶矩阵且|A|≠0,AC=CA,则
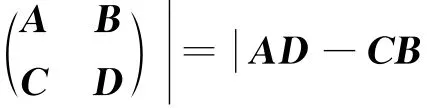
引理3[7-8]设A是一个n阶矩阵,对任何u,v∈Cn有
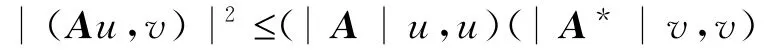
2 主要结论及证明
定理1 设A∈Cn×n,A是正规矩阵当且仅当
1)A与对角矩阵酉相似,即存在酉矩阵U∈Cn×n,使U*AU对角化.
2)A∈Cn×n,A=U|A|,A是正规矩阵当且仅当U与A可换.
3)λ1,λ2,...,λn是A的特征值且|λ1||λ2|,…,|λn|,则A是正规矩阵当且仅当|λ1(A)λ2(A)·…·λk(A)|=σ1(A)·…·σk(A), k=1,2,…,n.对于所有的k都成立.
4)A是正规矩阵当且仅当A的每个特征向量是A*的一个特征向量.
5)A是正规矩阵当且仅当和一个具有不同特征值的正规矩阵可换.
6)A是非奇异矩阵,M=A-1A*,证明A是正规矩阵当且仅当M是酉矩阵.
7)A是正规矩阵当且仅当I-A是正规的.
证 1)A是正规矩阵,则A*A=AA*
由定义1得,A=UDU*其中U∈Cn×n为酉矩阵,D为上三角阵.
则(U*AU)*(U*AU)=(U*AU)(U*AU)*,得A*A=AA*,A为正规矩阵.
2)A=U|A|, A=|A*|U,由于A*A=AA*,故|A|=|A*|
故U|A|=|A|U,U与A 可换;反之,U与A可换,则A=U|A|=|A|U=|A*|U,故|A|=|A*|A是正规的.
3)证明是显然的.
4)A是正规的,u是A的一个单位特征向量,特征值为λ,则存在酉矩阵U第一列为u,使得U*AU且α=0,取U*AU的共轭转置,u是A*的一个特征向量对应λ-是A*的特征值.另一方面,设Ax=λx(U*AU)(U*x)=λ(U*x)
U是n阶酉矩阵,由于Ax=λx由schur分解,假设A是一个上三角阵.
取e1=(1,0,…,0)T,e1是A的一个特征向量,假设e1也是A*的一个特征向量,A*e1=Ue1,A*的第一列由零组成除了第一个元素.因此
5)由于A和B可换,B是正规的,B的所有特征值不同,则B=V*CV,V为酉矩阵,C是对角阵diag(c1,c2,…,cn),AB=BA得WC=CW,W=(wij)=VAV*,wijci=wijcj,wij(ci-cj)=0,i≠j时ci≠cj,wij=0,因此是VAV*对角的,A是可以酉对角化的,故A是正规的.
反过来,B=Udiag(1,2,…,n)U*,显然可以得到B是正规的,AB=BA.
6)由于M=A-1A*,由A是正规的则A-1是正规的,故M*=A(A-1)*,M*M=A(A-1)*A-1A*=AA-1(A-1)*A*=In,故M是酉矩阵.反过来由于M是酉矩阵,则
M*M=In=A(A-1)*A-1A*,A-1In(A-1)*=A-1A(A-1)*A-1A*(A-1)*=(A-1)*A-1,
A-1(A-1)*=(A-1)*A-1,故A-1是正规的,显然A也是正规的.
7)由于A是正规的,则A*A=AA*
(I-A)*(I-A)=(I*-A*)(I-A)=(I-A*)(I-A)=I-A*-A+AA*
而(I-A)(I-A)*=I-A*-A+AA*
由于A*A=AA*,故(I-A)*(I-A)=(I-A)(I-A)*
故I-A是正规的.同理I-A是正规的,很容易可以得到A*A=AA*.
故A是正规的.
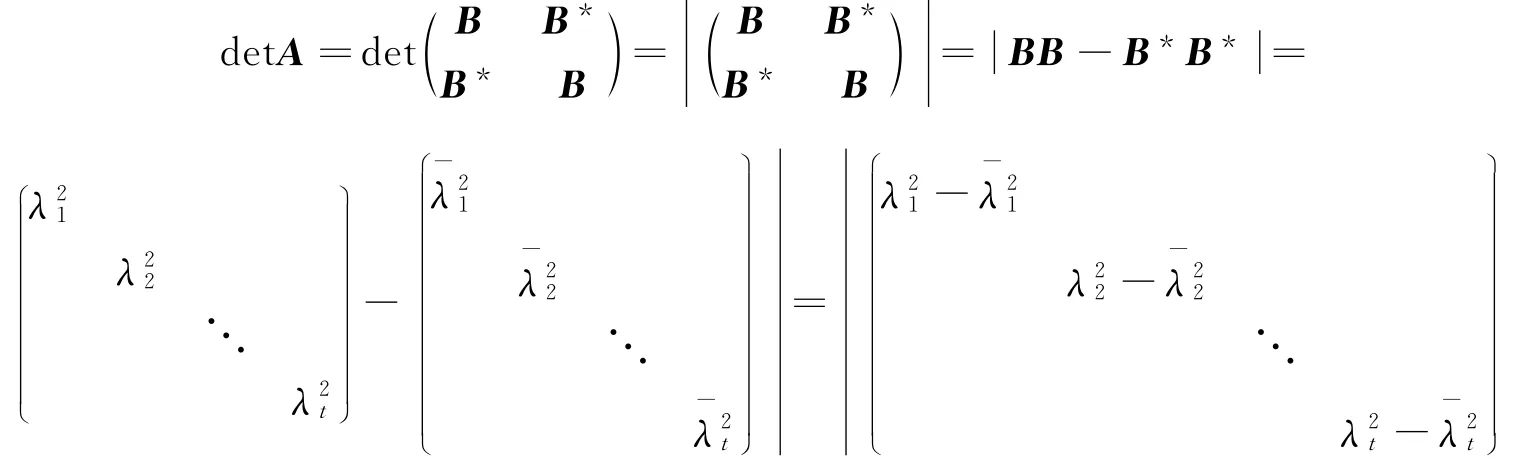
又由于λt=xt+yti,则λ-t=xt-yti,(xt,yt∈R,t=1,2,…,n),故
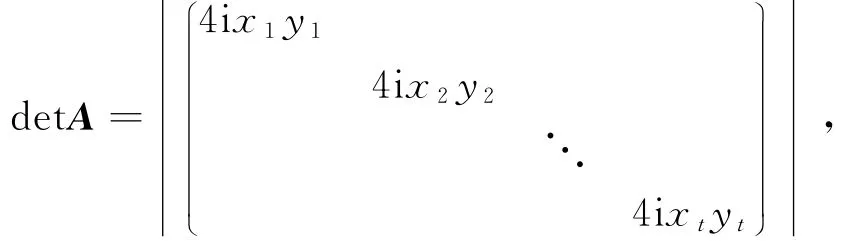
所以

定理3 设A=(aij)是一个n阶复矩阵,且λ1,λ2,…,λn为A的特征值.
2)若A是正规矩阵,则

3)若A和B是正规矩阵且AB是正规矩阵,则BA是正规矩阵
4)设A是正规矩阵,AB=BA,则A*B=BA*.
5)若A和B是正规矩阵,若AB=BA,则AB是正规的且存在一个酉矩阵U使得A和B同时对角化
6)设A是正规矩阵,则存在一个多项式P,使得
A*=P(A)
证 1)A=U*TU是A的schur分解,U是酉矩阵,T是上三角阵,则A*A=U*T*TU,显然tr(A*A)=tr(T*T)
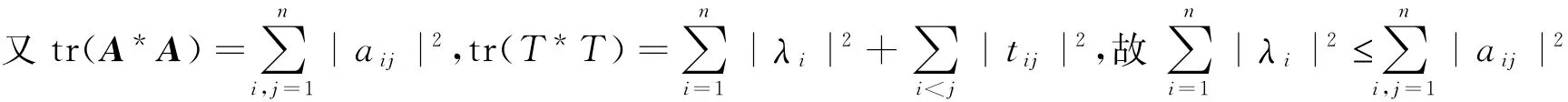
A正规时,T是对角的.等号显然成立.

且这种分解是唯一的.

则PkAQj=λkPkQj=λjPkQj,k≠j,则PkQj=0,Pj=PjIn=Pj(Q1+…+Qk)=PjQj

故Qj=Pj,分解是唯一的,称为A的谱分解.
3)设λ1(AB),λ2(AB),…,λn(AB)为AB的特征值.由于AB 的特征值和BA的特征值相同,又由于AB=

故A*B=BA*.
5)A和B是正规矩阵且AB=BA,由定理3的证明4)得A*B=BA*.
(AB)*(AB)=B*A*AB=B*AA*B=(A*B)*(A*B)
(AB)(AB)*=ABB*A*=AB*BA*=(BA*)*(BA*)
故AB是正规的.
由于A是正规的,则存在U使U*AU为对角阵,则
U*AUU*BU=U*BUU*AU,U*AU与U*BU可换,故U*BU为对角矩阵,定理得证.6)证明原理:设f是一个函数,f在不同的点λ1,λ2,…,λm的取值分别为b1,b2,…,bm.则
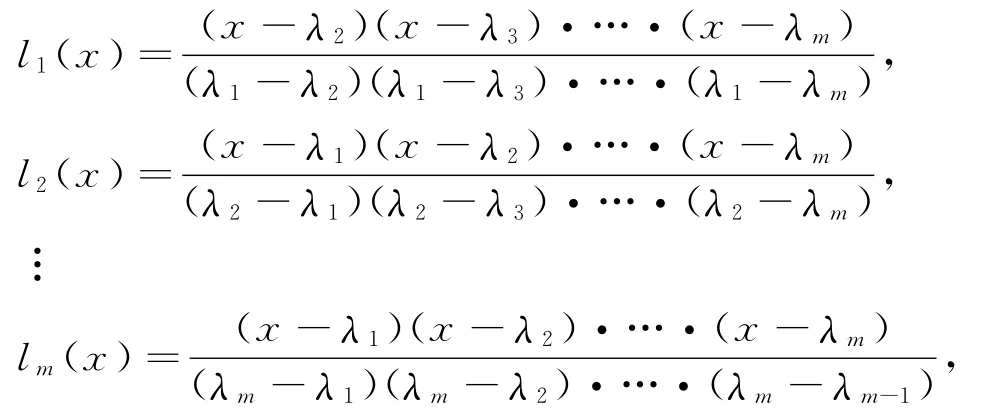
令P(x)=b1l1(x)+b2l2(x)+…+bmlm(x),p(λ1)=b1,…,p(λi)=bi不妨设A=diag(λ1,…,λn),使p(λi)=λi,i=1,2,…,n取不同的特征值.
则A*=P(A).
定理4 设A∈Cn×n,A是正规矩阵,则
1)tr(A*2A2)=tr[(A*A)2]
2)||Ax||=||A*x||,x∈Cn
3)若A是一个n阶方阵,则|(Au,u)|#(|A|2u,u).
4)A是正规矩阵当且仅当|(Au,u)|#(|A|u,u),u∈Cn
也有|(Au,u)|#(|A*|u,u),u∈Cn
证 1)由于||A*A-AA*||2F=2{tr[(A*A)2-(A*2A2)]}
又 ||A*A-AA*||2F=0
故 tr(A*2A2)=tr[(A*A)2];
2)||Ax||2=(Ax)*(Ax)=x*A*Ax=x*AA*x=||A*x||2
故||Ax||=||A*x||,x∈Cn
3)设A=UDV是A的奇异值分解,U和V为酉矩阵,D是非负对角阵,则|A|=V*DV,|A*|=UDU*.
4)由定义4得,A=U|A|
由定理2得,U与A 可换.因为|A|12是A 的多项式,则U和|A|12可换,则
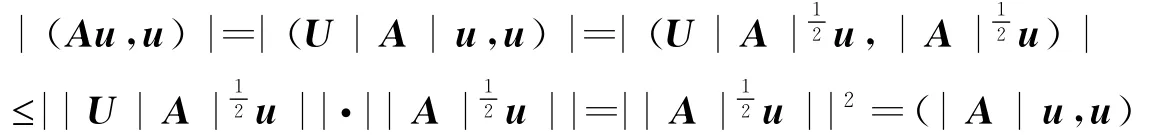
故有|(Au,u)|#(|A|u,u),u∈Cn
反过来,如果|(Au,u)|#(|A|u,u),u∈Cn,由schur定理假设A是上三角阵.
只需证明A是对角阵即可
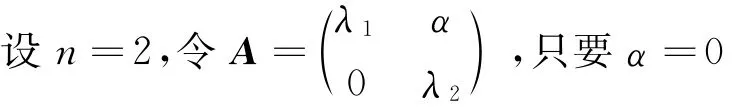
若λ1=λ2=0且α=0,取两个正数s,t,且s>t,u=(s,t)T,有
|u*Au|=st|α|,u*|A|u=t2|α|,|u*Au|#u*|A|u,(s<t)
若λ1≠0或者λ2≠0,令
则由|u*Au|#u*|A|u得|λ1|#a.
比较|A|2=A*A的左上角元素得a2+|b|2=|λ1|2,故b=0
这个矩阵的(1,2)元素得λ1α=(a+c)b=0,故α=0
因此A是对角阵,则A是正规的.
同理有|(Au,u)|#(|A*|u,u),u∈Cn.
参考文献:
[1]M P Drazin.On diagonable and normal matrices[J].Quart.J.Math.Oxford Ser,1951,2(2):189-198.
[2]M P Drazin,J W Dungey,K W Gruenberg.Some theorems on commutative matrices[J].J.London Math.Sot,1951,2(6):221-228.
[3]P M Gibson.Simultaneous diagonalization of rectangular complex matrices[J].Linear Algebra Appl,1974,9:45-53.
[4]F Hausdorff.Der Wertvorrat einer Bihnearform[J].Math,1919,2(3):314-316.
[5]Horn R A,Johnson C R.Matrix analysis[M].Cambridge:Cambridge University Press,1990.
[6]Horn R A,Johnson C R.Topics in matrix analysis[M].Cambridge:Cambridge University Press,1991.
[7]I Kaplansky.Products of normal operators[J].Duke Math,1953,2(2):257-260.
[8]C R Johnson.Normality and the numerical range[J].Linear AZgebra A&,1976,5(1):84-94.
Remarks on normal matrices
JIA Jie,REN Fangguo
(School of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China)
In this paper,using the normal matrix and the definition of eigenvalue and singular value,contact the spectral norm,Schur lemma,polar decomposition,unitary similar matrix and their equivalent characterizations of normal matrix,the properties of normal matrix eigenvalue and singular value relationship between eigenvalue and singular value respectively and the normal relationship between matrix eigenvalues and trace,and using mathematical analysis and analogy thought only
regular matrix decomposition,the inner product promotion and proves that.
normal matrix;eigenvalue;trace;norm
O152.21
A
1671-9476(2017)02-0014-06
10.13450/j.cnkij.zknu.2017.02.004
2016-07-18;
2016-11-25
国家自然科学基金资助项目(No.11471200)
贾杰(1990-),女,河南郑州人,硕士研究生,研究方向为矩阵论.
*通信作者简介:任芳国,陕西师范大学副教授,E-mail:rfangguo@snnu.edu.cn.

