一类整数阶与分数阶五维混沌系统的滑模同步

王建军，张 伟

（郑州航空工业管理学院理学院，河南郑州450015）

一类整数阶与分数阶五维混沌系统的滑模同步

王建军，张 伟

（郑州航空工业管理学院理学院，河南郑州450015）

基于Lyapunov稳定性理论及分数阶微积分的理论，研究了一类整数阶与分数阶五维混沌系统的滑模同步问题，研究表明选取适当控制律，主从系统是滑模混沌同步的，数值仿真说明该方法的有效性.

滑模同步；五维混沌系统；动力

混沌同步研究取得了很多成果［1－7］，文献［8］提出了一个四翼超混沌Lorenz系统，并对其动力学特征进行了分析.文献［9］在该系统上加入一个线性状态控制器构建了一个新的五维自治系统，并进行了其动力学分析.文献［10］对该系统进行了反同步研究，给出了数值仿真，文献［11］研究了非线性鲁棒控制理论.笔者研究整数阶与分数阶一个五维混沌系统的滑模同步问题，基于Lyapunov稳定性理论及分数阶微积分的理论，选取适当控制律，研究该五维混沌系统滑模同步问题，数值仿真说明该方法的有效性.

1 主要结果

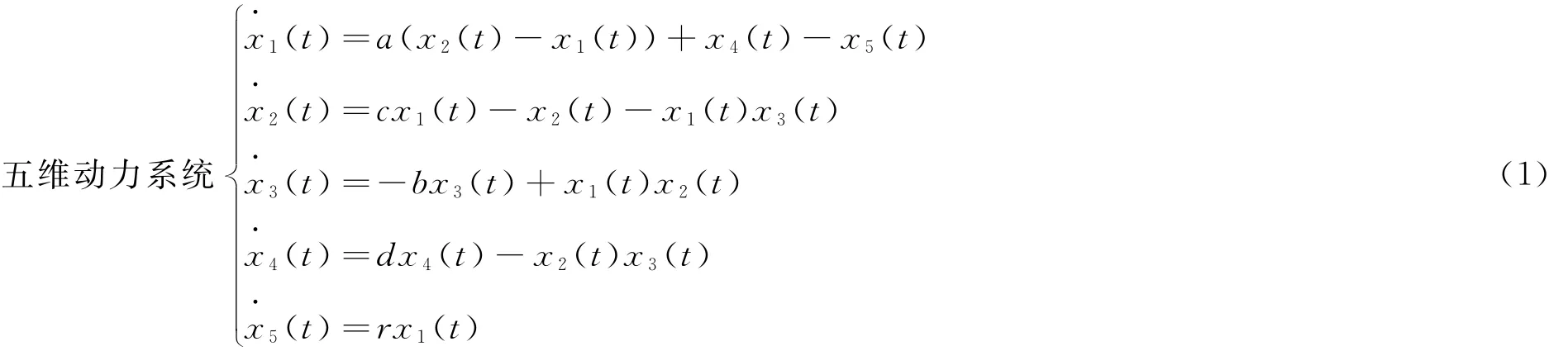
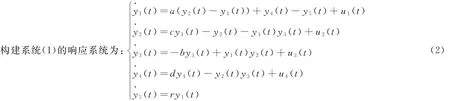
定义误差：ei（t）＝yi（t）－xi（t）（i＝1，2，3，4，5）那么

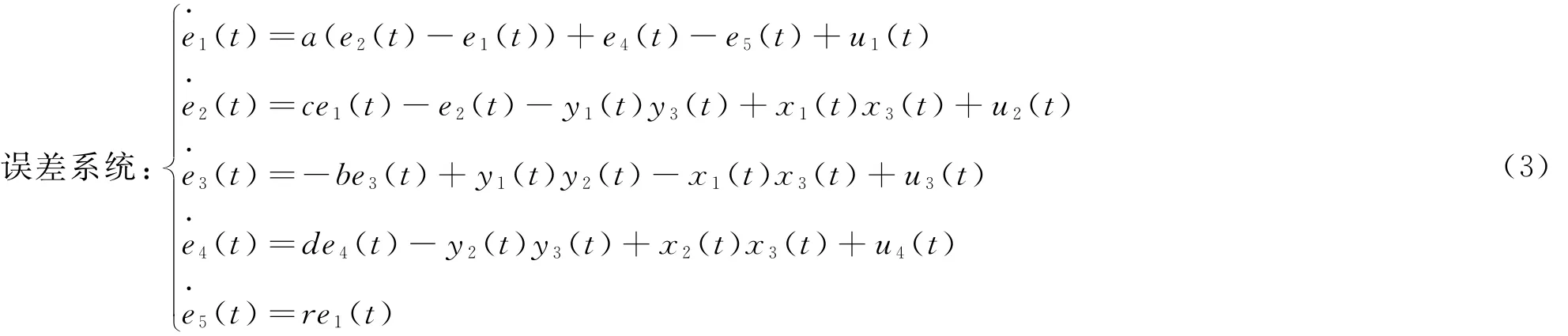
定理1 设计滑模面s（t）＝e1（t）＋e2（t）＋e3（t）＋e4（t）＋e5（t），选取控制律

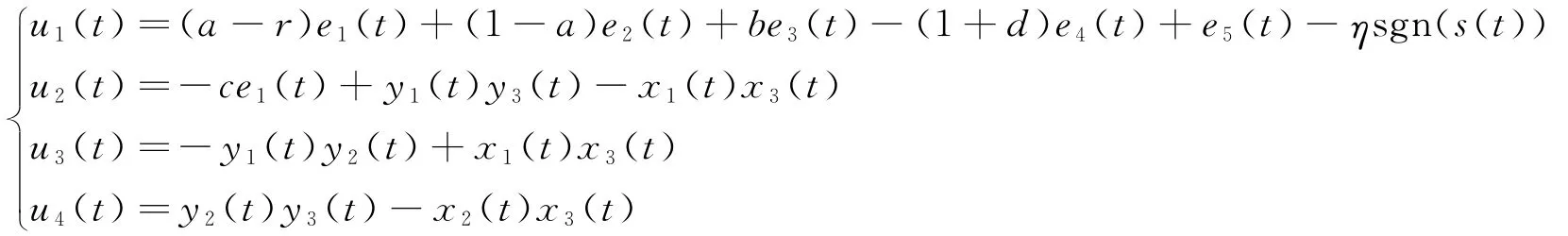
那么系统（1）和系统（2）是同步的.

证 当状态轨迹位于滑模面上时，s（t）＝0，s（t）＝0.由u2（t）＝－ce1（t）＋y1（t）y3（t）－x1（t）x3（t）同样可得

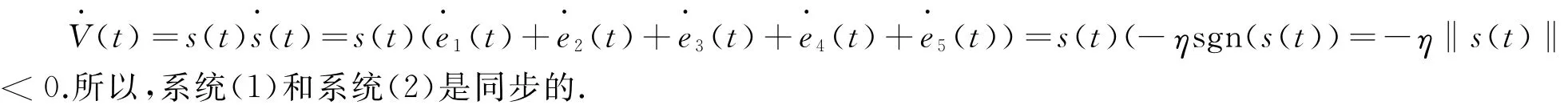
定义1［12－13］Caputo分数阶导数定义为：

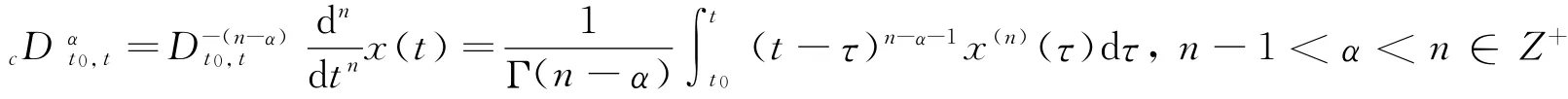
下面考虑分数阶动力系统

定理2 设计滑模面s（t）＝Dα－1t（e1（t）＋e2（t）＋e3（t）＋e4（t）＋e5（t）），选取控制律

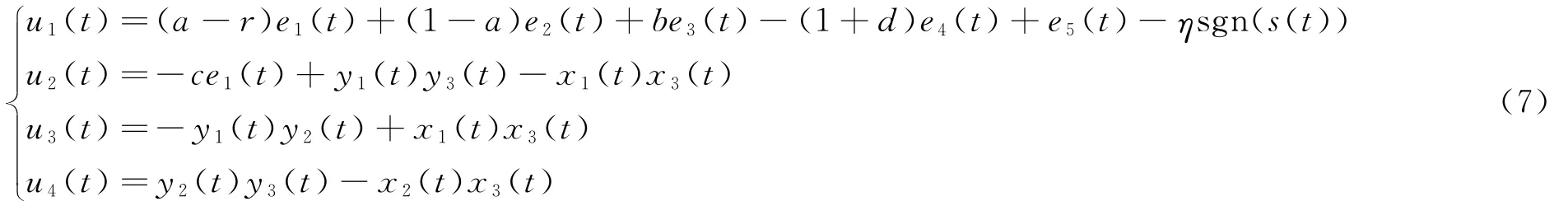
那么系统（4）和系统（5）是同步的.

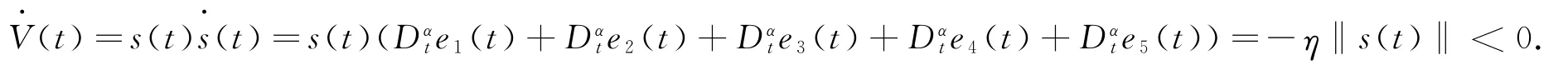
所以，系统（4）和系统（5）是同步的.

2 结束语

基于Lyapunov稳定性理论及分数阶微积分的理论研究了五维混沌系统滑模同步问题，研究表明：选取适当控制律，主从系统是滑模混沌同步的，数值仿真说明该方法的有效性.

［1］李洁，黄艳宾，石丁丁，等.多涡卷系统的有限时间滑模控制［J］.科技通报，2015，31（1）：183－185.

［2］王欢，王思聪.带有干扰观测器的分数阶滑模控制［J］.电光与控制，2015，22（5）：89－92.

［3］邢伟，茅青海.受周期外界环境影响的Van der pol情绪模型［J］.数学建模及其应用，2016，5（1）：43－48.

［4］达飞鹏，宋文忠.基于输入输出模型的模糊神经网络滑模控制［J］.自动化学报，2000，21（1）136－139.

［5］刘文峰，杨小冈，缪栋，等.基于模糊滑模的有限时间混沌同步实现［J］.物理学报，2007，56（11）：6250－6257.

［6］Pecoral LM，Caarol TL.Synchronizationof chaotic systems［J］.Phys.Rev.Lett.，1990，64（8）：821－830.

［7］Carrol TL，Pecoral LM.Synchronization chaotic circuits［J］.IEEE Trans.Circuits systems，1991，38（4）：453－456.

［8］王兴元，王明军.超混沌Lorenz系统［J］.物理学报，2009，56（9）：5136－5141.

［9］魏亚东，周爱军.一个新五维超混沌系统的动力学分析［J］.舰船电子工程，2012，32（7）：68－71.

［10］魏亚东.新五维超混沌系统反同步研究［J］.舰船电子工程，2012，32（11）33－37.

［11］梅生伟，申铁龙，刘志康.现代鲁棒控制理论与应用［M］.北京：清华大学出版社，2003.

［12］Podlubny.Fractional differential equation［M］.New York：Academic Press，1999.

［13］胡建兵，赵灵冬.分数阶系统稳定性理论与控制研究［J］.物理学报，2013，62（24）：5041－5047.

The sliding mode synchronization of a class of
five-dimension integer-order and fractional-order systems

WANG Jianjun，ZHANG Wei
（College of Science，Zhengzhou Institute of Aeronautical Industry Management，Zhengzhou 450015，China）

The problem of the sliding mode synchronization of a class of five-dimension integer-order and fractional order systems is studied based on Lyapunov stability theory and the theory of fractional-order calculus.The conclusion is arrived that masterslave systems are chaos synchronized under appropriate controlling law.Numerical simulations of chaotic system verify the effectiveness of the proposed method.

sliding mode synchronization；five-dimension systems；dynamics

O482.4

A

1671-9476（2017）02-0007-03

10.13450／j.cnkij.zknu.2017.02.002

2016-07-21；

2016-10-12

国家自然科学青年基金（No.NSFC11501525）；河南省科技厅软科学项目（No.142400411192）

王建军（1978－），男，山东枣庄人，讲师，硕士，主要研究方向：复杂网络与混沌同步.Email：wjj123789＠126.com