含三个忆阻器的六阶混沌电路研究∗

王伟 曾以成 孙睿婷

(湘潭大学物理与光电工程学院,湘潭 411105)

含三个忆阻器的六阶混沌电路研究∗

王伟 曾以成†孙睿婷

(湘潭大学物理与光电工程学院,湘潭 411105)

(2016年8月26日收到;2016年11月23日收到修改稿)

利用两个磁控忆阻器和一个荷控忆阻器设计了一个六阶混沌电路,并建立了相应电路状态变量的非线性动力学方程.研究了系统的基本动力学特性,平衡点及其稳定性分析表明：该电路具有一个位于忆阻器内部状态变量所构成三维平衡点集,平衡点的稳定性由电路参数和三个忆阻器的初始状态决定.分岔图、Lyapunov指数谱等表明该电路在参数变化情况下能产生Hopf分岔和反倍周期分岔两种分岔行为,以及超混沌、暂态混沌、阵发周期现象等多种复杂的非线性动力学行为.将观察混沌吸引子时关注的电压、电流信号推广到功率和能量信号,观察到了莲花型、叠加型吸引子等奇怪吸引子的产生.并研究了各忆阻器能量信号之间产生吸引子的情况,特别地,当取不同的初始值时,系统出现了共存混沌吸引子和周期极限环与混沌吸引子的共存现象.

忆阻器,六阶混沌电路,浮地,动力学

1 引 言

2008年,美国HP实验室[1,2]首次在物理上成功地实现了基于金属和金属氧化物的忆阻器,并建立其相应的数学模型,证实了1971年蔡少棠根据电路变量的完备性原理所做的预测[3].由于忆阻器的记忆性及其非线性等特性使其在神经网络[4]、非易失性阻抗存储器(RRAM)[5]、电路设计等[6,7]领域有着潜在的应用价值,也成为非线性科学领域的一个新的研究热点[8-11].忆阻器构成的电路容易产生高频混沌振荡信号,因此在图像加密[12]、保密通信等[13]领域将具有广泛的应用前景.2008年,Itoh和Chua[14]采用一个磁控分段线性忆阻器来替换蔡氏电路中的二极管导出第一个基于忆阻器的混沌系统,接着针对含一个忆阻器的混沌电路有一系列工作[15-19].包伯成等[20]提出含两个三次光滑模型磁控忆阻的五阶混沌电路,得出了含两个忆阻器的混沌电路其平衡点对应一个平面;Buscarino等[21]采用两个相互并联的磁控忆阻器替换蔡氏二极管得到新混沌电路;洪庆辉等[22]利用荷控和磁控两种忆阻器模型设计了一个五阶混沌电路,仿真分析表明含两个忆阻器的混沌振荡电路具有更加复杂的拓扑结构并拥有更丰富的混沌动力学行为.

由于含三个甚至更多个忆阻器的混沌电路研究较少,现有的忆阻混沌电路都为四阶和五阶这样的低阶混沌电路,且多为针对如类蔡氏系统这样的特定系统,这样对高阶复杂混沌电路的研究自然就有了较大的价值.而现有的六阶甚至更高阶混沌电路主要是基于蔡氏电路电容耦合或者耦合两个低阶混沌电路的方法构造而成,其研究的目的都只是为了研究混沌控制与同步.那么是否能通过多个忆阻器来实现高阶混沌系统呢?如果构建含三个忆阻器的六阶混沌电路,它将具有一个更为复杂的位于三个忆阻器内部状态变量所构成三维立体空间上的平衡点集,再加上高阶电路拥有更加丰富的电路参数和更复杂的动力学行为,其应用于混沌保密通信中将更加难以破译.为此,本文利用两个磁控忆阻器和一个荷控忆阻器设计含三个忆阻器的新型六阶混沌电路,电路接法上结合忆阻器与电感串联、电容并联以及浮地型三种形式,这样将更加符合电路的一般化设计.利用理论推导研究它的平衡点集,结合相图、分岔图、Lyapunov指数谱等非线性分析手段分析系统的动力学特性.通常观察混沌吸引子时都是关注的电压、电流以及磁通之间的特性,而没有报道过与功率和能量信号之间的特性,本文从功率和能量信号去探索其吸引子的产生,并详细研究各忆阻器能量信号之间的关系,最后,将通过改变初始状态去探索该系统能否产生共存吸引子.

2 忆阻器模型

作为一个无源二端口元件,忆阻器的磁通φ与累积的电荷量q之间的关系可以用φ-q或q-φ平面上的一条曲线来确定,忆阻器分为磁控型和荷控型两种[1-3].荷控忆阻器磁通随电荷量的变化率为：M(q)=dφ(q)/dq,流过的电流与两端的电压之间的伏安特性的表达式为v=M(q)i,其中M(q)称为忆阻;磁控忆阻器电荷随磁通的变化率为W(φ)=dq(φ)/dφ,流过的电流与两端的电压之间的伏安特性的表达式为i=W(φ)v,其中W(φ)称为忆导. 这里的M(q)和W(φ)均是取决于忆阻器内部状态变量φ或q的非线性函数.

常用的忆阻器模型有分段线性型(PWL)、二次或三次光滑型,本文均采用三次光滑忆阻器模型.即荷控忆阻器模型为

可得其忆阻为

其中a,b为常量.磁控型忆阻器模型及其忆导分别为

其中c,d为常量.

3 基于三个忆阻器设计的混沌电路

一个新型六阶忆阻混沌电路如图1所示,该电路主要由三个部分组成：一个磁控忆阻器与电容并联,一个荷控忆阻器与电感串联,另一个磁控忆阻器单独且浮地.电路由2个磁控忆阻器、1个荷控忆阻器、2个电容和1个电感这六个动态元件构成,其对应的六个状态变量分别为：φ1,φ2,q,v1,v2和iL,其中φ1,φ2和q是三个忆阻器的内部状态变量.

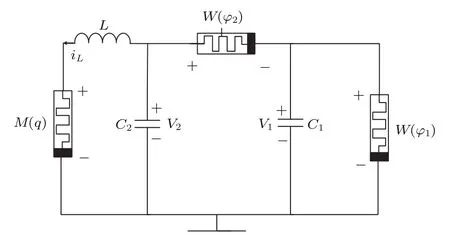
运用基尔霍夫定律(KVL及KCL)以及元器件的伏安特性分析图1所示电路,可以得到如下六个联立的一阶微分方程组：

为了便于进行数值分析,将方程组(5)进行变量代换,设x=v1,y=v2,z=iL,u=φ1,v=φ2,ω=q,δ=1/C1,β=1/C2,γ=1/L.方程组可以重写为

式中：M(ω)=a+3bω2,W(u)=c+3du2,W(v)=e+3fv2;其中a,b,c,d,e,f为常量.选择电路参数δ=9,β=1,γ=12;忆阻器参数a=0.01,b=0.03,c=-1.2,d=1,e=0.9,f=0.9,初始状态取值为(0.1,0,0.1,0,0,0).利用六维龙格-库塔算法,仿真得到系统的相空间或相平面的投影如图2所示,可以看到系统生成了一个双涡卷吸引子.采用Jacobi方法计算Lyapunov指数谱得LE1=0.2777,LE2=0.0069,LE3=-0.0023,LE4=-0.0008,LE5=-0.0004,LE6=-6.3380.系统(6)的Lyapunov维数DL=5.0444.由系统的相轨迹、Lyapunov指数、Lyapunov维数可知系统是混沌振荡的.选取不同变量的Poincaré截面如图3所示,可以看到Poincaré截面上有较为明显的分形结构密集点并且吸引子的轮廓清晰可见,进一步说明此系统是混沌振荡的.

图2 典型的混沌吸引子相图 (a)x-y-z平面;(b)x-z平面;(c)u-x平面;(d)u-y平面Fig.2.Phase portraits of typical chaotic attractor：(a)Onx-y-zplane;(b)onx-zplane;(c)onu-xplane;(d)onu-yplane.

图3 Poincaré截面 (a)Poincaré映射在x-z上的投影;(b)Poincaré映射在u-y上的投影Fig.3.Section of Poincaré：(a)Poincaré projection onx-z;(b)Poincaré projection onu-y.

4 系统的基本动力学特性

4.1 系统平衡点及其稳定性分析

令(6)式各微分方程右边为零,可得系统平衡点集为

即六维空间中u-v-ω三维子空间的任一点都是该系统的平衡点,(7)式中k1,k2,k3为实常数.当取电路参数δ=9,β=1,γ=12;忆阻器参数a=0.01,b=0.03,c=-1.2,d=1,e=0.9,f=0.9,选择k1,k2和k3作为可调参数,将新系统在平衡点处线性化可求得Jacobi矩阵,然后根据平衡点集S对应的特征根方程可知系统(6)含有6个特征根：3个非零特征根和3个零特征根.最后,依据Routh-Hurwitz稳定条件,计算可得：

当k2=0,k3=0,则在k1-k2-k3构成三维立体的k1坐标轴上对应不稳定的范围是

当k1=0,k3=0,则在k1-k2-k3构成三维立体的k2坐标轴上对应不稳定的范围是

当k1=0,k2=0,则在k1-k2-k3构成三维立体的k3坐标轴上对应不稳定的范围是

选取初始状态值(0.1,0,0.1,u(0),v(0),ω(0))中的u(0),v(0)和ω(0)作为三个可变参数.当v(0)=0,ω(0)=0时,系统(6)随初始值u(0)=k1变化的Lyapunov指数谱如图4(a)所示.同理,随初始值v(0)=k2,ω(0)=k3变化的Lyapunov指数谱分别如图4(b)和图4(c)所示.图4中考虑到图片的清晰度,故舍去了第5根Lyapunov指数曲线的部分和第6根Lyapunov指数曲线.

图4 随初始状态变化的Lyapunov指数谱 (a)随k1变化的Lyapunov指数谱;(b)随k2变化的Lyapunov指数谱;(c)随k3变化的Lyapunov指数谱Fig.4.The Lyapunov exponent spectra changing with initial state：(a)The Lyapunov exponent spectra changing withk1;(b)the Lyapunov exponent spectra changing withk2;(c)the Lyapunov exponent spectra changing withk3.

不同于一般的忆阻混沌系统,系统(6)的平衡点由磁控和荷控两种忆阻器的初值状态决定,从不同区域出发的运行轨线将有着不同的动力学行为.该系统的稳定性不仅受平衡点集S的三个非零特征根影响,而且其另外三个零特征根在一定的电路参数取值下也会对其动力学特性产生影响.对比图4所示的Lyapunov指数谱和上述理论分析结果不难发现,在区间-0.249＜k2＜-0.105,0.105＜k2＜0.249,-0.556＜k3＜-0.2以及0.18＜k3＜0.556不同,在这几个区间内系统为稳定的汇,主因是受平衡点集S三个零特征根的影响.还有一个值得指出的现象是,图4(a),图4(b)和图4(c)中分别有区间0＜k1＜0.2,-0.1＜k2＜0.1,-0.1＜k3＜0.2中存在两个大于的Lyapunov指数,该六阶混沌电路出现了超混沌现象,即随着初始状态的改变,系统存在着从普通混沌到超混沌的转变过程.

4.2 随电路参数变化的动力学分析

系统参数的改变将会改变平衡点的稳定性,这将引起系统状态的变化.对于上述确定的参数条件下,选择电路参数γ作为控制参数,利用Lyapunov指数谱结合分岔图和不同具体参数下的相轨图来分析电路参数对该混沌系统的影响.当电路参数γ在区间[10,15]变化时,系统的Lyapunov指数谱和分岔图如图5所示.为了更清晰地呈现非负Lyapunov指数,因此在绘图5(a)时舍去了第5根的数值较小部分和第六根Lyapunov指数曲线.

对比图5(a)和图5(b)不难看出,图中各自运行轨线所体现系统稳定与不稳定状态区域相互符合.系统是失稳突然进入混沌的,即通向混沌的道路为Hopf分岔[23],然后又经反倍周期分岔逐步退出混沌最终成为一个有界点.由图5(b)可知,γ=10.5为Hopf分岔临界点.当γ＜10.5时,系统相轨道为极限环,当γ＞10.5系统进入混沌态.当10.5≤γ＜14.25时,系统出现两个大于的Lyapunov指数,即发生了超混沌行为.当14.25≤γ≤ 15时,系统历经周期4、周期2、周期1极限环最终进入稳态.系统(6)产生的周期轨和混沌轨在u-y平面的投影如图6所示.图6(a)与图6(b)反映了系统Hopf分岔通向混沌行为;图6(b)和图6(c)分别出现单涡卷与双涡卷超混沌吸引子,与图5(a)中呈现的最大Lyapunov指数为正的区间相对应;图6(d),图6(e)与图6(f)印证了分岔图中系统反倍周期分岔走出超混沌的过程.表1中列出了电路参数γ在各个变化区间所对应的不同动力学行为.

图5 随电路参数γ变化时的Lyapunov指数谱和分岔图 (a)Lyapunov指数谱;(b)分岔图Fig.5.The Lyapunov exponent spectra and bifurcation diagram changing with the circuit parameterγ：(a)Lyapunov exponent spectra;(b)bifurcation diagram.

表1 电路参数γ在区间[10,15]的系统动力学行为Table 1.system dynamic behavior of circuit parameterγin interval[10,15].

图6 随电路参数γ变化时在u-y平面上的相图 (a)γ=10.35(周期1);(b)γ=10.6(双涡卷超混沌吸引子);(c)γ=13.9(单涡卷超混沌吸引子);(d)γ=14.35(周期4);(e)γ=14.4(周期2);(f)γ=14.8(周期1)Fig.6.Phase portraits onu-yplane with the change of circuit parameterγ：(a)γ=10.35(period-1);(b)γ=10.6(double scroll hyperchaotic attractor);(c)γ=13.9(single scroll hyperchaotic attractor);(d)γ=14.35(period-4);(e)γ=14.4(period-2);(f)γ=14.8(period-1).

4.3 暂态混沌与阵发周期现象

在上述分析改变电路参数的动力学参数条件下,当γ=10.51时,系统在有限时间尺度内出现混沌,即暂态混沌现象.从图7(b)可以看出,在最初演化的t=1.5×104内系统的状态是混沌的,对应图7(a)中间部分的双涡卷混沌吸引子,但随着时间的推移,当t＞1.5×104时,y的波形幅度呈现拟周期态,对应图7(a)中轨迹由中间的双涡卷混沌吸引子逐步向外扩展达到外延的轨迹边界.整个过程是随着时间的演化,系统由混沌态逐渐转化为拟周期态,此为暂态混沌现象.其产生原因是由于随着控制参数的变化,相空间中混沌吸引子与其吸引盆之间的边界距离不断减小,直到在一个临界值彼此相遇.此时该混沌吸引子触及到一个不稳定的周期轨道而导致了边界危机的发生.

当γ=13.89时,系统出现了稳态混沌伴随阵发周期行为的奇异现象.图8显示了不同平面的伴随阵发周期5的稳态混沌吸引子,即在混沌中共存一个周期5阵发周期轨道.经过大量的数值仿真,结果表明,此现象的出现不仅依赖于电路参数,同时对系统的初始条件也是极端敏感的.

图7 暂态混沌现象 (a)u-y平面;(b)y的时域波形图Fig.7.Transient chaos phenomenon：(a)Onu-yplane;(b)time domain waveform ofy.

图8 伴随阵发周期的稳态混沌行为 (a)u-x平面;(b)u-y平面Fig.8.With the period of intermittent steady chaotic behavior：(a)Onu-xplane;(b)onu-yplane.

4.4 随忆阻器初始状态变化的动力学分析

通常情况下,忆阻混沌系统对初始条件具有敏感依赖性[24],在含有三个忆阻器的混沌系统中,选择系统初始状态值(0.1,0,0.1,0,0,ω(0))中的ω(0)=k作为整个系统的控制参数,其在区间[0,0.25]变化的Lyapunov指数谱与分岔图如图9所示.图9(a)从图片清晰度考虑,舍去了第5根的数值较小部分和第6根Lyapunov指数曲线,可以观察到Lyapunov指数谱和分岔图是基本符合的.如图9所示,当0≤k≤0.17时,系统Lyapunov指数形式为(+,+,0,0,0,-),表明系统在此区间发生了超混沌行为,能产生混沌吸引子.当0.17＜k≤0.22,此时系统处于周期状态,而当k＞0.22,此时系统进入稳态.

图9 随初始状态时的Lyapunov指数谱和分岔图 (a)Lyapunov指数谱;(b)分岔图Fig.9.The Lyapunov exponent spectra and bifurcation diagram changing with initial state：(a)Lyapunov exponent spectra;(b)bifurcation diagram.

5 探索吸引子

5.1 奇怪吸引子与叠加型吸引子

通常观察混沌吸引子时都是关注的电容的电压、电感的电流以及忆阻器的磁通之间的特性,如果将其推广到功率和能量信号将会产生什么现象呢?如图10所示,取功率和类能量信号作为独立信号,图10(a)反映的是q与电感L的功率特性图,其相图为一个四涡卷混沌吸引子;图10(b)和图10(c)呈现的分别是v2,iL与忆阻器W(φ2)的能量间的特性,其中相图10(b)为莲花型吸引子;图10(d)体现iL与荷控忆阻器M(q)的能量特性,其产生的吸引子为一个像四翼的蝴蝶型吸引子.

固定原系统参数不变,改变电路参数δ,对比参数分别取δ=7.65与δ=9.05时产生v2与电感L的功率特性图.如图11所示,两个吸引子的不同之处在于,图11(b)中的吸引子为图11(a)中的吸引子的叠加而成,本文将其称为叠加型吸引子.

图10 奇怪吸引子 (a)q-P(L);(b)v2-W(W(φ2));(c)iL-W(W(φ2));(d)iL-W(M(q))Fig.10.Strange attractor：(a)q-q-P(L);(b)v2-W(W(φ2));(c)iL-W(W(φ2));(d)iL-W(M(q)).

图11 叠加型吸引子 (a)叠加前相图;(b)叠加后相图Fig.11.Superposition type attractor：(a)Superimposed front phase diagram;(b)superimposed phase diagram.

图12 刻画忆阻器能量信号间的相轨图 (a)i-v;(b)W(W(φ1))-W(W(φ2));(c)W(W(φ1))-W(M(q));(d)W(W(φ2))-W(M(q))Fig.12.Phase portraits for depicting between the memristor energy：(a)i-v;(b)W(W(φ1))-W(W(φ2));(c)W(W(φ1))-W(M(q));(d)W(W(φ2))-W(M(q)).

图13 共存现象 (a)共存混沌吸引子;(b)混沌吸引子与周期2极限环共存;(c)周期2极限环与周期1极限环共存;(d)共存周期1极限环Fig.13.Phenomenon of coexistence：(a)Coexisting chaotic attractor;(b)coexistence of chaotic attractor and limit cycle with period-2;(c)coexistence of limit cycle with period-2 and period-1;(d)coexisting limit cycle with period-1.

5.2 探索各忆阻器间的能量信号

取各忆阻器的能量信号作为独立信号,探索各忆阻器能量信号间的关系,如图12所示.图12(a)反映的是忆阻器W(φ2)两端的i-v特性图,体现出了忆阻器斜“8”字的记忆特性.图12(b)—(d)分别呈现了各忆阻器能量信号之间产生的吸引子,从图中可以看出,两忆阻器的能量信号之间都能产生奇怪吸引子.其吸引子的形状有点像忆阻器斜“8”字的记忆特性图,产生该现象的原因与忆阻器本身的记忆特性有关.

5.3 共存吸引子

固定原系统δ,γ的值,初始值分别取(0.1,-0.1,-0.1,0,0,0)和(-0.1,-0.1,-0.1,0,0,0),当β取合适参数,能够观察到φ1与忆阻器W(φ1)的能量信号间产生共存吸引子现象,如图13(a)所示.当β=3.06时,系统出现了共存混沌吸引子现象,且两吸引子相互对称即对称吸引子.当β=3.25时,产生了混沌吸引子与周期2极限环共存现象,其对应图13(b).而当β分别取3.6和4.0时,系统能分别产生周期2极限环与周期1极限环共存和共存周期1极限环现象,如图13(c)和图13(d)所示.该结果表明,在相空间中有着相互独立的混沌吸引盆和准周期吸引盆.在忆阻混沌系统中共存现象有过少数报道,但还未在能量信号中研究其共存吸引子的产生.

6 总 结

利用具有光滑特性曲线的磁控和荷控两种忆阻器模型,结合忆阻器与电容并联、电感串联和浮地型三种电路接法构造了一个六阶混沌电路,使用常规动力学研究方法对其特性进行了相应的理论分析.研究表明,含三个忆阻器的混沌电路具有一个位于忆阻器内部状态变量所构成三维空间上的平衡点集,并定性分析了该平衡点集的稳定性空间分布,采用相轨图、Lyapunov指数谱以及分岔图等动力学分析手段验证了理论分析的正确性.将观察混沌吸引子时关注的电压、电流以及磁通之间的特性推广到了功率和能量信号,观察到了莲花型、叠加型吸引子等奇怪吸引子的产生,并研究了三个忆阻器的能量信号之间产生的吸引子相图.特别地,当初始状态不同时,系统在能量信号关系中出现了共存混沌吸引子或周期极限环与混沌吸引子的共存现象.尽管该系统产生的超混沌、暂态混沌、阵发周期等复杂动力学行为在已有文献报道,但这些现象都出现在了同一个忆阻混沌系统中尚不多见.本文提出的忆阻混沌电路丰富了忆阻器在高阶混沌电路中的应用,对其进行深入研究具有重要的理论意义和工程应用价值.由于在一定的电路参数下,该电路的稳定性同时受平衡点集的三个非零特征根和三个零特征根影响,并对电路参数和系统初始值具有很强的敏感性,较其他混沌系统具有更多的电路参数和更加复杂的拓扑结构,拥有更丰富的混沌动力学行为,提高了混沌系统的复杂度及其产生信号的随机性.因此应用于混沌保密通信中加密的信息更难破译,将拥有更好的保密性能和安全性能.

[1]Strukov D B,Snider G S,Stewart D R,Williams R S 2008Nature453 80

[2]Tour J M,He T 2008Nature453 42

[3]Chua L O 1971IEEE Trans.Circ.Theory18 507

[4]Wu A L,Zeng Z G 2012Neural Networks36 1

[5]Duan S K,Hu X F,Wang L D,Li C D 2012Sci.China:Inf.Sci.55 1446

[6]Li Q D,Zeng H Z,Li J 2015Nonlinear Dyn.79 2295

[7]Hong Q H,Li Z J,Zeng J F,Zeng Y C 2014Acta Phys.Sin.63 180502(in Chinese)[洪庆辉,李志军,曾金芳,曾以成2014物理学报63 180502]

[8]Chua L O 2011Appl.Phys.A102 765

[9]Wang L,Yang C H,Wen J,Gai S 2015J.Mater.Sci.26 4618

[10]Yuan F,Wang G Y,Wang X W 2016Chaos26 073107

[11]Chua L O 2015Radioengin24 319

[12]Lin Z,Wang H 2010IETE Tech.Rev.27 318

[13]Min G Q,Wang L D,Duan S K 2015Acta Phys.Sin.64 210507(in Chinese)[闵国旗,王丽丹,段书凯 2015物理学报64 210507]

[14]Itoh M,Chua L O 2008Int.J.Bifurc.Chaos18 3183

[15]Muthuswamy B,Kokate P P 2009IETE Tech.Rev.26 417

[16]Muthuswamy B,Chua L O 2010Int.J.Bifurc.Chaos20 1567

[17]Bao B C,Liu Z,Xu J P 2010Chin.Phys.B19 030510

[18]Li Z J,Zeng Y C 2013Chin.Phys.B22 040502

[19]Bao B C,Hu F W,Liu Z,Xu J P 2014Chin.Phys.B23 070503

[20]Bao B C,Shi G D,Xu J P,Pan S H 2011Sci.China:Tech.Sci.41 1135(in Chinese)[包伯成,史国栋,许建平,刘中,潘赛虎2011中国科学：技术科学41 1135]

[21]Buscarino A,Fortuna L,Frasca M,Valentina G L 2012Int.J.Non.Sci.22 023136

[22]Hong Q H,Zeng Y C,Li Z J 2013Acta Phys.Sin.62 230502(in Chinese)[洪庆辉,曾以成,李志军2013物理学报62 230502]

[23]Benhabib J,Nishimura K 1979J.Econ.Theory21 421

[24]Bao B C,Xu J P,Liu Z 2010Chin.Phys.Lett.27 070504

PACS:05.45.—a DOI:10.7498/aps.66.040502

Research on a six-order chaotic circuit with three memristors∗

Wang WeiZeng Yi-Cheng†Sun Rui-Ting

(School of Physics and Optoelectronic Engineering,Xiangtan University,Xiangtan 411105,China)

26 August 2016;revised manuscript

23 November 2016)

A memristor is a nonlinear nanoscale-sized element with memory function,and it has an italic type “8” voltagecurrent relation curve that looks like a pinched hysteresis loop characteristic.The memristor is utilized to construct chaotic circuit,which has attracted the attention of the researchers.At present,most of studies focus on applying one or two memristors to the chaotic circuit.In order to study the multi memristor chaotic circuit,in this work we propose a sixorder chaotic circuit with two flux-controlled memristors and a charge-controlled memristor.A corresponding six-order nonlinear dynamic differential equation of the circuit state variables is established.The dynamic properties of the circuit are demonstrated in detail.The analyses of equilibria and equilibrium stability show that the circuit has an equilibrium located in the three-dimensional space which is constituted by memristor internal state variables,and it is found that the equilibrium stability is determined by the circuit parameters and the initial states of three memristors.The Lyapunov exponent spectra and bifurcation diagrams of the circuit imply that it can produce two bifurcation behaviors by adjusting its parameters,which are Hopf bifurcation and anti-period doubling bifurcation.The hyperchaos,transient chaos and intermittency cycle phenomena are found in the same system.The dynamical behavior of this circuit is dependent on the initial state of memristor,showing different orbits such as chaotic oscillation,periodic oscillation and stable sink under different initial states.Finally,the simulation results indicate that some strange attractors like lotus type and superposition type are observed when voltage and electricity signal in observing chaotic attractors are generalized to power and energy signal,respectively.And the attractor production between the energy signals of the memristors are studied.Specially,when different initial conditions of three memristors are used to simulate the circuit,we can find the coexistence phenomenon of chaotic attractors with different topological structures or quasi-periodic limit cycle and chaotic attractor.

The six-order chaotic oscillating circuit is mainly composed of three parts:the parallel connection between aflux-controlled memristor and capacitor,the serial connection between a charge-controlled memristor and inductor,and another flux-controlled memristor that is alone and floating,which enriches the application of memristor in highorder chaotic circuit.Compared with most of other chaotic systems,it has many circuit parameters and very complex topological structure,which enhances the complexity of chaotic system and the randomness of the generated signal.It is more difficult to decipher the encrypted information in chaotic secure communication,and thus it has better security performance and safety performance.

memristor,six-order chaotic circuit,floating,dynamics

:05.45.—a

10.7498/aps.66.040502

∗国家自然科学基金(批准号：61471310)资助的课题.

†通信作者.E-mail：yichengz@xtu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant No.61471310).

†Corresponding author.E-mail：yichengz@xtu.edu.cn