透射光学系统像平面一阶散射光照度分布规律研究∗
谭乃悦 许中杰 韦可 张月 王睿
(国防科学技术大学光电科学与工程学院,长沙 410073)
透射光学系统像平面一阶散射光照度分布规律研究∗
谭乃悦 许中杰 韦可 张月 王睿†
(国防科学技术大学光电科学与工程学院,长沙 410073)
(2016年6月16日收到;2016年11月16日收到修改稿)
透射光学系统由于结构简单、成本低、视场大、成像质量高等优点,广泛应用于探测、显微、望远等实际应用中,但目前关于该类系统像平面散射光斑分布规律的研究却鲜见报道.本文对透射光学系统焦平面散射光照度分布规律展开研究,以Harvey双向散射分布函数散射理论为基础,建立了小散射角条件下透射光学系统一阶表面散射光在像平面的高斯函数分布规律的理论模型,该模型能与实验数据很好地符合.
Harvey散射,透射光学系统,一阶表面散射,高斯函数
1 引 言
随着大功率激光器和相机技术的发展,关于表面散射理论的研究成果层出不穷[1-9].从目前已有的文献来看,国内外对于表面散射的研究主要集中在反射表面散射上,然而对于广泛应用于探测、显微、望远等实际工程应用中的透射光学成像系统的表面散射研究却鲜见报道,其主要原因一方面是因为反射表面散射测量仪器原理简单,易于操作;另一方面是因为国内外对于表面散射主要是作为材料表面特性来研究,而不是研究光学系统整体的散射状况.关于透射光学系统中表面散射在焦平面的成像规律,目前仅有2参数的Harvey双向散射分布函数(bi-directional scatter distribution function,BSDF)散射模型[10]的报道,存在着在散射角度较小时与实际情况不符的缺陷,而对于聚焦透射光学系统而言,小角度散射对于焦面成像质量的影响尤为显著.本文以Harvey BSDF散射理论为基础,建立小散射角度条件下透射光学系统一阶表面散射光在像平面的高斯函数分布规律的理论模型,该模型与2参数Harvey BSDF散射模型互为补充,拓宽了Harvey BSDF散射模型的适用范围,使之能够更好地解释透射光学系统像平面散射光斑的成像规律.该模型的建立弥补了2参数Harvey BSDF散射理论的局限性,为后续小散射角度的表面散射研究提供有效的理论依据.
2 理论模型
2.1 光学表面散射
如图1所示,当一束光照射某光学元件时,由于光学元件材料表面高度的随机起伏使得入射到该表面的部分能量将在反射定律或者折射定律确定的方向以外传播,称之为散射光.
表面散射是由材料表面高度的起伏导致的.在传播过程中,某表面产生的一次散射光称之为一阶散射光,一阶散射光还可能会被其他表面再一次散射,形成二次散射乃至多次散射,这些二次散射及多次散射被称为二阶散射及高阶散射.相对于入射波长,表面高度的起伏越大,表面就越“粗糙”,被散射的能量份额(即散射能量在总透射能量中所占的比例)就越大.材料表面的“粗糙”程度可用其表面高度的均方根粗糙度[11](root-mean-square roughness,rms粗糙度,记为σrms)来衡量.本文重点研究经过抛光的光学表面的散射,这类表面的rms粗糙度约在1—50 nm之间.
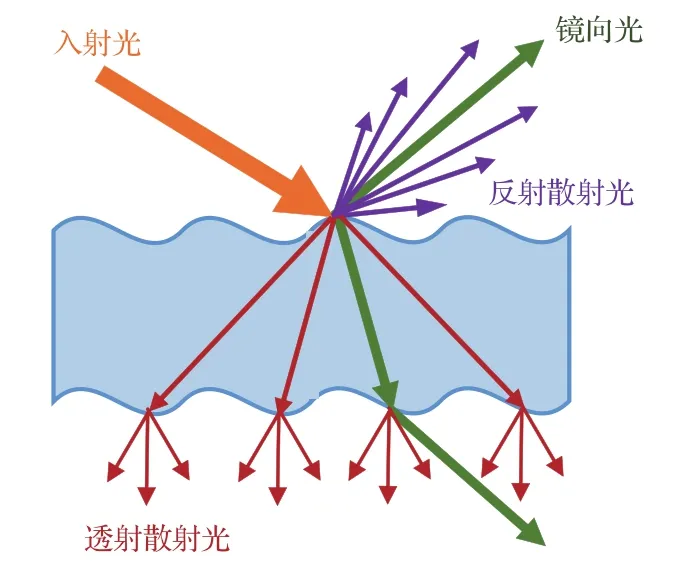
图1 (网刊彩色)表面起伏与表面散射示意图Fig.1.(color online)Schematic of the surface undulation and surface scattering.
全积分散射(total integrated scattering,TIS),定义为透射散射功率与总透射功率的比值,且由其与表面rms粗糙度的关系[12],有
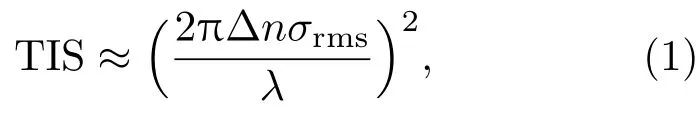
其中Δn为材料两边的折射率差.透射光学系统按其应用谱段可分为可见光和红外光学系统,可见光学系统通常使用的光学材料是SiO2,其折射率约为1.5,而红外光学系统通常使用的光学材料是Ge,Si和ZnS等,它们在红外波段的折射率约在2—4之间,而空气的折射率近似为1,则材料两边的折射率差约为Δn=1—3.例如本文实验中使用的光学系统的透镜材料主要为Si,其折射率约为3.4268,则材料两边的折射率差Δn=2.4268,若取Δn=2.4268,σrms=50 nm,λ=3.8µm,则TIS为4.0%.由全积分散射可知,二阶散射能量大约只占一阶散射能量的4.0%,且二阶散射能量分散在整个透射半球空间,因此二阶散射对最终像面散射光斑辐照度的贡献相对一阶散射要弱很多.为了简化,本文仅考虑表面对光线的一阶散射.
2.2 Harvey BSDF模型
经过大量的实验测量,Harvey发现对于干净的、光滑的、各向同性的光学表面,散射亮度具有线性平移不变性,如图2所示.
根据上述实验现象,Harvey提出了2参数的Harvey BSDF模型.数学上,其可以写成如下形式[10]:
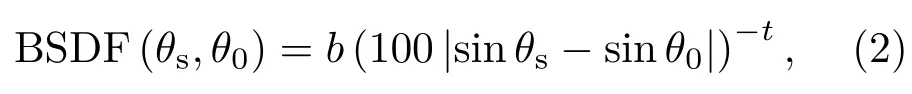
其中θ0是折射角,θs是散射角,b是偏离折射方向0.01 rad处的BSDF的值,t为对数坐标系下的斜率的绝对值.一般地,b和t的值可以从实验测量得到.对于干净的、光滑的光学表面,t的典型取值范围为1<t<3.
由(2)式可知,当散射角度较小时,即|sinθs-sinθ0|→0时,BSDF≫1,显然不符合实际情况.
针对上述情况,为了避免BSDF的数值在折射方向上变成无限大,本文引进了一个肩下降参数l进行修正,其单位为弧度(rad),其定义为在对数坐标系下,随着|sinθs-sinθ0|的减小,散射模型的BSDF值从某一点处开始趋向一个常数时,则该点的横坐标值为肩参数l.假定b0是散射角θs等于θ0时BSDF的值,此时b0应为BSDF的最大值,令b0=b(100l)-t,则当|sinθs-sinθ0|≤l时,由(2)式可知,BSDF≥b0,与b0为BSDF的最大值矛盾,不符合实际情况.
近年来,Harvey等在将Harvey BSDF模型推广到适用于更一般的表面散射的过程中发现,实验测量所得的表面散射的BSDF曲线与几个高斯函数之和拟合得很好[13,14].因此我们也不妨假设,当|sinθs-sinθ0|≤l时,即散射角度较小时,表面散射的BSDF曲线呈指数分布,由肩下降参数l的定义以及在对数坐标系下当|sinθs-sinθ0|≫l时BSDF曲线的斜率的绝对值趋向t(这里是为了与2参数的Harvey BSDF模型的t保持一致),建立了散射角度较小时的高斯函数分布的BSDF模型,其具体的数学形式如下:
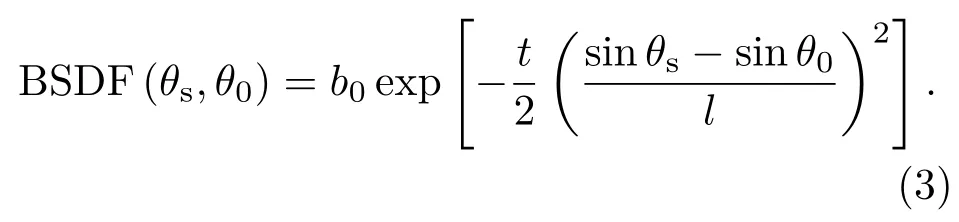
比较(2)式和(3)式,改进后的BSDF模型可写为
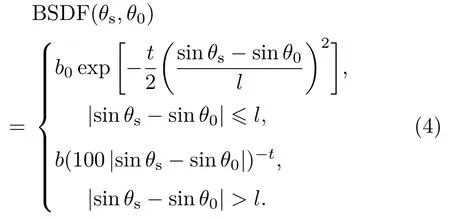
2.3 理论模型的建立
Peterson[15]利用Lagrange不变量来表示相对散射角以及使用能量守恒定律来描述散射能量传递时,最终推导得出:对于聚焦透射光学系统,最终像面上由某表面的散射而产生的辐照度分布与该表面的BSDF成正比,即
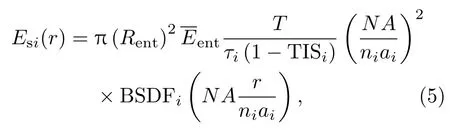
其中,r为最终像面上的点到像面中心的距离,NA是系统的像方数值孔径,T为系统的总透射率,τi和TISi分别为第i表面的半球透射率和全积分散射,入射光束的光功率为E=π(Rent)2ent,ni和ai分别为入射光透过第i表面时的折射率和有效光束半径.
如果该系统有n个表面,则表面散射在最终像面上P点的辐照度是所有表面散射在该处的贡献之和,即
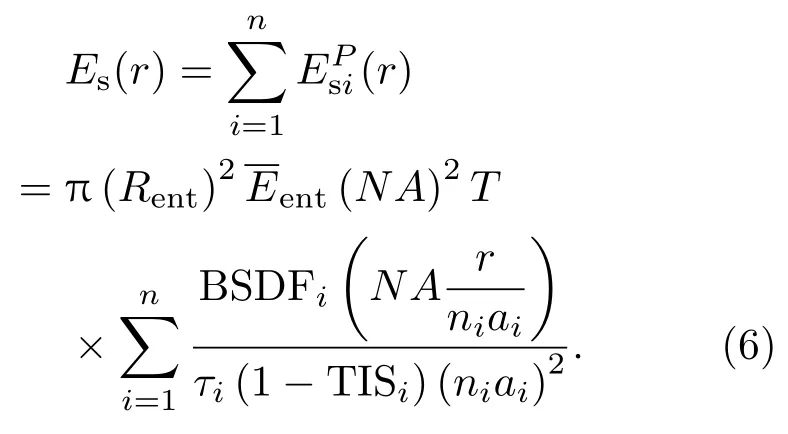
当入射光功率密度较大时,散射导致的饱和区(详见3.3节)较大,此时落在饱和区边缘的散射光的散射角相对较大,当|sinθs-sinθ0|>l时,由(4)式得
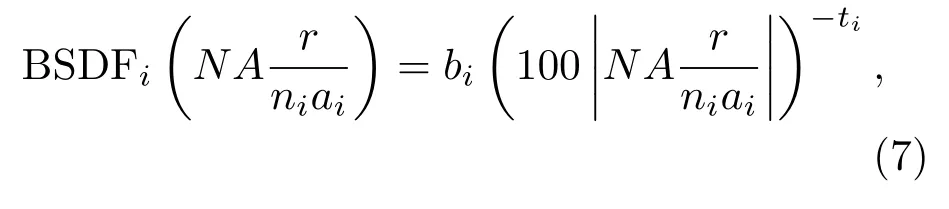
其中bi是散射角为0.01的BSDFi的值.假设每个表面的BSDFi中的ti均相等,即ti=t,将(7)式代入(6)式并化简,有
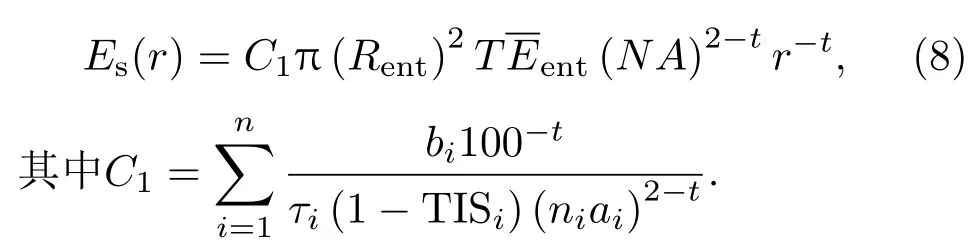
当入射光功率密度较小时,散射导致的饱和区较小,此时落在饱和区边缘的散射光的散射角相对较小,当|sinθs-sinθ0|≤l时,根据(4)式有
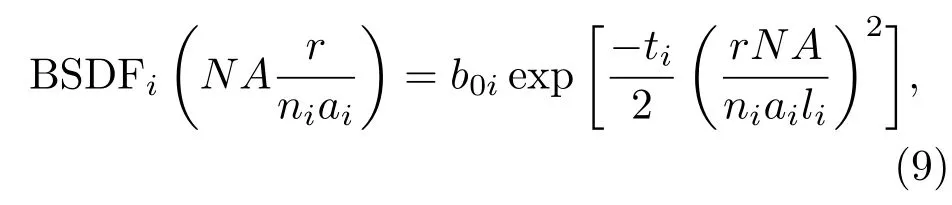
其中b0i是散射角为0的BSDFi的值.将(9)式代入(6)式,有
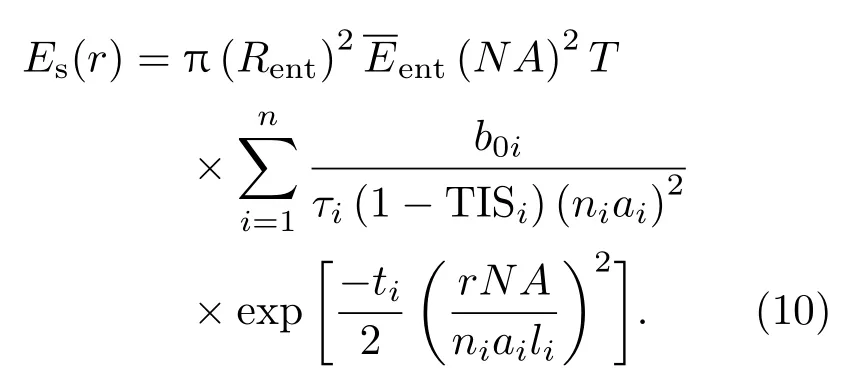
由(10)式可知,对于聚焦透射光学系统,小光功率密度条件下最终像面上散射光斑的辐照度分布可以表示为n个高斯函数之和.
2.4 衍射的影响
研究表明,对于理想的无像差系统,当平行光束沿光轴满瞳入射时,在像平面上接收到的衍射可以等效为圆形孔径的夫琅和费衍射(本文实验中所使用透镜均为圆形透镜),且在距离中心像点较远处的衍射光强按到几何像点距离的3次方衰减[16],具体如下:
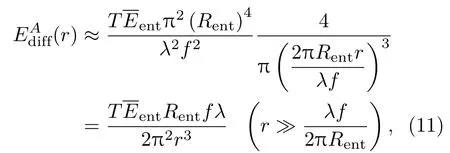
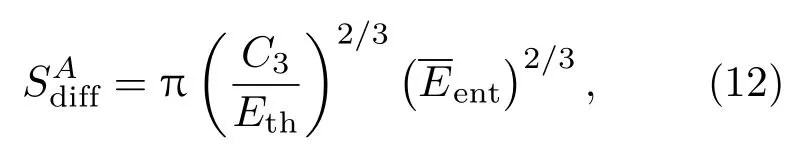
其中C3=TRentfλ/(2π2).(12)式说明由孔径衍射导致的探测器饱和区域面积SAdiff与入射光功率密度ent的2/3次方成正比.这个关系可用来估算由孔径衍射导致的饱和区域的面积随平均入瞳功率密度的变化规律.然而,实验发现,饱和区域的面积随入射光功率密度的变化不符合上述规律,对此,本文将在3.3节进行讨论.
3 实验研究
3.1 透射光学系统结构
为了验证改进的BSDF模型的合理性,我们采用四透镜的光学系统开展验证性实验,如图3所示,其中四个的透镜表面采用的是相同的加工工艺,因此我们可以近似地认为所有的光学表面拥有相同的表面粗糙度.

图3 (网刊彩色)透射光学系统结构图Fig.3.(color online)Structure arrangements of four lens system.
3.2 实验方法
实验光路如图4所示.本文采用的探测器为广泛应用于热成像、气体分析、FTIR光谱仪、激光探测、铁路Hotbox、线扫描仪激光光谱仪等领域的320×256面阵碲镉汞中红外探测器,其响应波段为3—5µm,工作温度为80 K.光源选用的是3.8µm的中红外连续激光器,经扩束后沿光轴方向满瞳入射到透射光学系统,激光经透射光学系统的传播到达探测器表面,在其表面形成一定的光强分布,记为E(x,y).探测器接收这种分布的光信号,产生光电效应,将光信号转换成电信号,再经过信号处理电路的作用,转换成图像信号V(x,y).
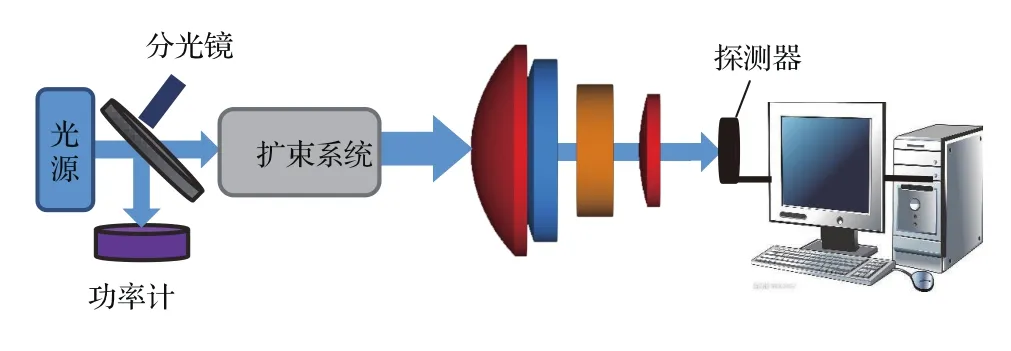
图4 实验光路示意图Fig.4.Schematic of the transmission optical system.
本实验主要关注激光在透射光学系统中传播时所经历的表面散射对探测器表面上的光强分布E(x,y)的影响.
3.3 实验结果与分析
在探测器表面,当某点的辐照度E(x0,y0)大于探测器饱和阈值Eth时,该点将会饱和,转换成图像信号输出为明亮的白点.图5给出了激光从视场内入射到透射光学系统时探测器的典型饱和图像.图中间的近似圆形的白色区域,其像素灰度值已经达到最大值,故称为饱和区.
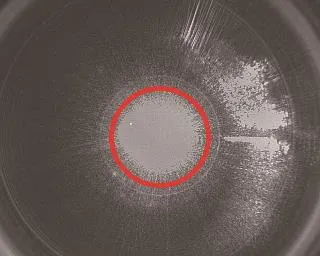
图5 (网刊彩色)典型的焦面光斑图像Fig.5.(color online)Typical spot image at the focal plane.
本实验重点关注的是红色圆圈内的饱和区随入射光功率变化的规律.通过统计红色圆圈内饱和像元的个数再乘以像元面积得到中心饱和光斑面积,记为Sth.
当入射光功率较大时,令Es(r)=Eth,代入(8)式得光学表面散射导致的饱和区域面积为

其中C2=T(NA)2-t.
假设只存在衍射,由(12)式可知,
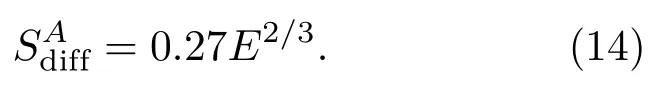
当入射光功率密度较大时,中心饱和光斑面积Sth(单位:mm2)随入射光功率E(单位:mW)变化的实验结果如图6中的黑色数据点,根据图6中的实验数据,对比2参数Harvey BSDF模型,可得到图6中蓝色曲线的数学表达式为
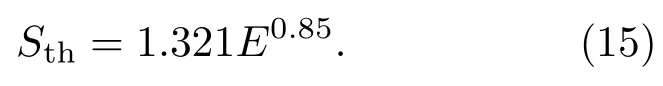
对比(13)与(15)式,可知
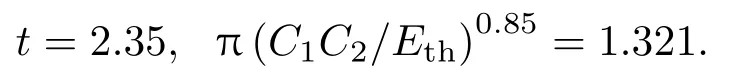
由孔径衍射导致的饱和区域的面积随入射光功率的变化曲线如图6中的黑色曲线所示,从图6给出的数据结果可以看出,纯衍射模型给出的结果与实验数据相差很大,因此除了衍射之外,还存在表面散射,且衍射远小于表面散射.同时,也可以看到2参数Harvey BSDF模型在描述大散射角情况下与实验数据符合得较好.
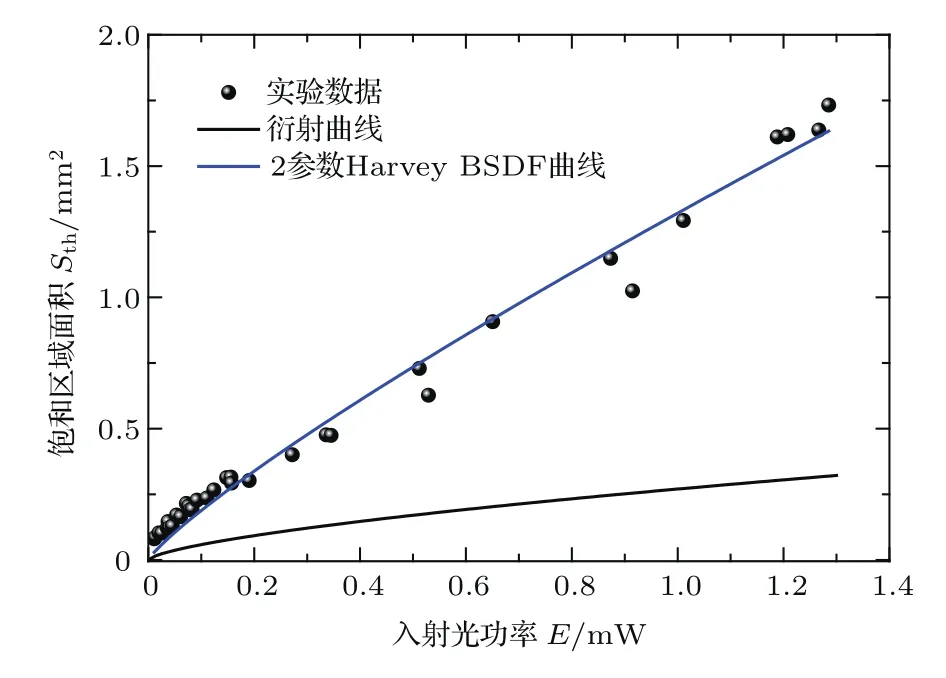
图6 入射光功率密度较大时饱和区域面积Sth随入射光功率E变化Fig.6.The saturated areaSthas a function of irradiation powerEin the condition of large irradiation power.
当入射光功率较小时,由BSDF的互易性原理[17],假设每个表面niaili=l,ti=t,代入(10)式,有
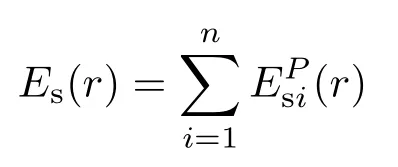
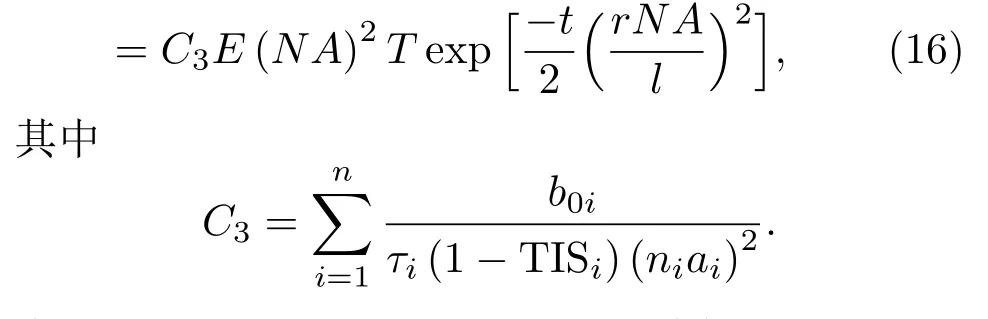
令Es(r)=Eth,得到由光学表面散射导致的饱和区域面积为
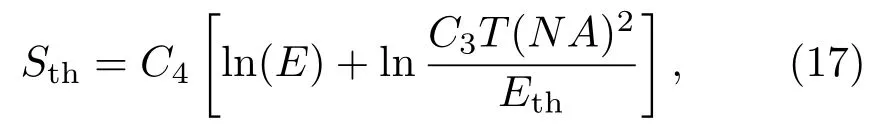
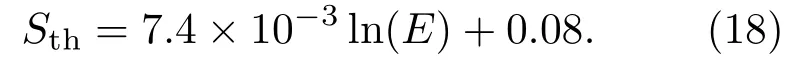
当入射光功率密度较小时,中心饱和光斑面积Sth(单位:mm2)随入射光功率E(单位:mW)变化的实验结果如图7中黑色的数据点.假设只存在衍射,由(14)式可知,由孔径衍射导致的饱和区域的面积随入射光功率的变化曲线如图7中黑色曲线所示,与实验数据相差很大.因此除了衍射之外,还存在表面散射,且衍射远远小于表面散射.
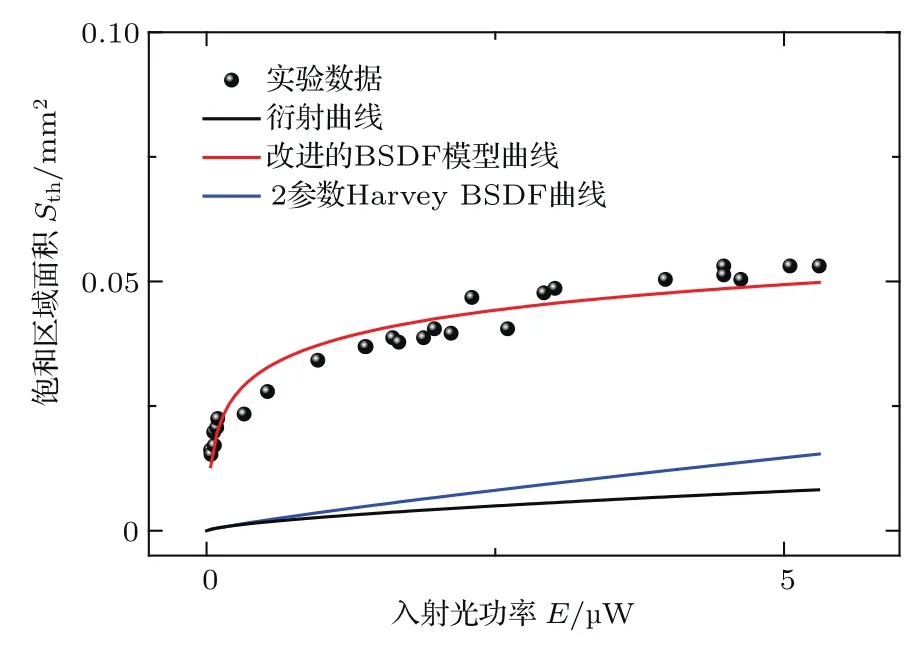
图7 (网刊彩色)入射光功率密度较小时饱和区域面积Sth随入射光功率E变化Fig.7.(color online)The saturated areaSthas a function of irradiation powerEin the condition of small irradiation power.
图7中红色曲线和蓝色曲线分别为基于改进的BSDF模型推导而来的(18)式和基于2参数Harvey BSDF散射模型推导而来的(15)式在小散射角条件下饱和区域面积Sth随入射光功率E变化的曲线.
对比蓝色曲线与实验数据,可以看出2参数Harvey BSDF散射模型在小散射角条件下与实验结果存在较大差距.
对比红色曲线与实验数据,可以看出改进后的BSDF散射模型与实验结果符合较好,从而验证了改进模型的合理性.
4 结 论
本文以Harvey BSDF散射理论为理论基础,在研究透射光学系统焦平面一阶散射光照度分布规律过程中发现了2参数Harvey BSDF散射理论在处理透射光学系统表面散射过程中存在的局限性,即小散射角条件下,2参数Harvey BSDF散射理论并不能准确地描述光学表面材料的散射特性.随后通过引入修正参数l,建立小散射角条件下透射光学系统的散射理论模型,并通过实验验证了该理论模型的准确性.在小散射角条件下,利用该理论模型可以得到以下结论:1)最终像面散射光斑辐照度的大小随入射光功率的增加线性增大;2)透射光学系统中每一个相同散射性质的光学表面对最终像面散射光斑辐照度贡献可以用一个高斯函数表示;3)最终像面散射光斑的辐照度可以表示为n个高斯函数的叠加,其中n为透射光学系统中不同散射性质光学表面的数目.
[1]Jiang Y S,Nie M Y,Zhang C H,Xin C W,Hua H Q 2015Acta Phys.Sin.64 024101(in Chinese)[江月松,聂梦瑶,张崇辉,辛灿伟,华厚强2015物理学报64 024101]
[2]Nicodemus F E,Richmond J C,Hsia J J,Ginsberg I W,Limperis T 1977Geometrical Considerations and Nomenclature for Reflectance(Washinton,D.C.:National Bureau of Standards)pp7-8
[3]Dereniak E L,Brod L G,Hubbs J E 1982Appl.Opt.21 4421
[4]Hu D J,Zhang Z Y,Du J L 2015Chin.Phys.B24 104202
[5]He Y,Wu J 1997Acta Opt.Sin.17 1202(in Chinese)[何毅,吴健1997光学学报 17 1202]
[6]Liu M,Cheng C F,Ren X R 2015Chin.Phys.B24 094202
[7]Fan D 2013Acta Opt.Sin.33 267(in Chinese)[范镝2013光学学报33 267]
[8]Zhang J B,Ding L,Wang Y P,Zhang L,Wu J L,Zheng H Y,Fang L 2016Chin.Phys.B25 034201
[9]Huang H L,Chen Z Y,Sun C Z,Liu J L,Pu J X 2015Chin.Phys.Lett.32 104202
[10]Harvey J E 1976Ph.D.Dissertation(Arizona:University of Arizona)
[11]Stover J C 1990Optical Scattering:Measurement and Analysis(New York:McGraw-Hill)pp23-44
[12]Bennett H E,Porteus J O 1961JOSA51 123
[13]Harvey J E,Vernold C L,Krywonos A,Thompson P L 1999Appl.Opt.38 6469
[14]Harvey J E,Goshy J J,Pfisterer R N 2014Proc.SPIE9205 01
[15]Peterson G L 2004Proc.SPIE5178 184
[16]Sun K,Jiang H M,Cheng X A 2011Opt.Precision Engineer.19 493(in Chinese)[孙可,江厚满,程湘爱 2011光学精密工程19 493]
[17]Veach E 1997Ph.D.Dissertation(California:Stanford University)
PACS:42.25.Fx,42.30.—d,42.30.Lr DOI:10.7498/aps.66.044201
The research on the illumination distribution law of thefirst-order scattered light in the focal plane of transmission optical system∗
Tan Nai-YueXu Zhong-Jie Wei KeZhang YueWang Rui†
(College of Opto-Electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China)
16 June 2016;revised manuscript
16 November 2016)
With the advantages of simple structure,low-cost,large field of view,and high image quality,the transmission optical system is widely used in detection system,microscope,telescope,etc.However,the research on the illumination distribution law in the focal plane of transmission optical system is rarely reported.In this paper,this issue is studied.During the study on the first-order scattered light distribution law in the focal plane of the transmission optical system,the limitations of the two-parameter Harvey bi-directional scatter distribution function(BSDF)scattering theory are found,namely in the condition of small scattering angle,the two-parameter Harvey BSDF theory cannot accurately describe the scattering properties of the optical surface material.So the scattering model of the transmission optical system under small scattering angle is established by introducing parameterl,and the accuracy of the new theoretical model is verified experimentally.This model complements the two-parameter Harvey BSDF scattering model and broadens the application scope of the Harvey BSDF scattering model so that it can better explain the imaging law of scattered light spot in the focal plane of transmission optical system.At a small scattering angle,the conclusions can be drawn from the new theoretical model as follows.1)The irradiance of the final image plane increases linearly with the increase of the incident optical power.2)In the transmission optical system,the contribution of each optical surface with the same scattering properties to scattered spot irradiance in the final image plane can be expressed by a Gaussian function.3)The irradiance of scattered spot in the final image plane can be expressed as the superposition ofnGaussian functions,wherenis the number of optical surfaces with different scattering properties in the transmission optical system.
Harvey BSDF scattering theory,transmission optical system,focal plane spot first-order surface scattering,Gaussian distribution
:42.25.Fx,42.30.—d,42.30.Lr
10.7498/aps.66.044201
∗激光与物质相互作用国家重点实验室(批准号:SKLLIM1402)资助的课题.
†通信作者.E-mail:xi_g_z@126.com
*Project supported by the Open Basic Research of the State Key Laboratory of Laser Interaction with Matter,China(Grant No.SKLLIM1402).
†Corresponding author.E-mail:xi_g_z@126.com

