运用四元数分析椭球微粒所受的光阱力∗
张书赫 梁振 周金华
(安徽医科大学生物医学工程系,合肥 230032)
运用四元数分析椭球微粒所受的光阱力∗
张书赫 梁振†周金华‡
(安徽医科大学生物医学工程系,合肥 230032)
(2016年10月3日收到;2016年10月17日收到修改稿)
在光镊的射线模型中,追迹光线在界面的折射反射光是较基本的也是较复杂的问题.传统的几何光学法计算光线的方位,对于一些不规则的物体来说,存在一定的困难度.本文提出使用四元数简化空间光线追迹,从而可计算非球形颗粒的光阱力.以入射光线和界面法线的外积确定入射面的法线为旋转轴;根据折射定律确定由入射光线旋转到反射光线和折射光线的角度.将入射光线以四元数表示,根据四元数旋转,可获得反射光线和折射光线的空间矢量.根据光子的动量变化,求得光阱对微粒的作用力.本文以球差影响下的不同形变的椭球为计算示例,模拟了椭球在光阱下的动力学行为,结果表明椭球的横向和轴向俘获效率受到各方向变形系数的影响;球差增大降低了轴向的最大俘获效率,稳定俘获位置也随之朝负轴偏离中心更远;在固定球差作用下,最大轴向俘获效率与轴向变形系数相关,在特定的变形下轴向俘获效率变得较大.由此验证了四元数方法的正确性、实用性与普遍性.
四元数,光线追迹,椭球微粒,光阱力
1 引 言
目前光镊广泛应用于单分子检测马达蛋白[1,2],DNA和RNA力学特性分析[3]、测量细胞膜弹性[4]和探测溶液的黏弹性[5]等方面.在光镊应用中,光阱对不同颗粒的作用,以及如何低功率下获得高光阱力一直吸引许多研究者不断探索[6].在前人的光阱模拟和实验中,光束的类型[7]、束腰半径[8]、颗粒大小[9]和聚焦光束的数值孔径[10]均会影响光阱力的大小.光阱力的模拟方法一直备受关注,可帮助我们更深入理解光阱俘获小球的动力学行为,还可指导我们设计光镊提升俘获效率.
光阱力的模拟方法大致有两类,一类是几何光学模型(或者射线模型,ray optics,RO);另一类方法为电磁模型(electromagnetic model,EM).RO模型的算法原理简单,适于模拟颗粒尺寸远大于波长的光阱力,即使在颗粒尺寸与波长相近时,也能取得与实验相近的结果,在光镊发展的30年内不断得到应用和推广.
在RO模型中,Ashkin[11]提出的射线追踪的模型可以很好地分析球形颗粒在光阱中的受力,并可进一步模拟玻璃-水界面引起球差对光阱力的影响[12,13],以及双光纤夹持颗粒的受力[14].然而采用欧氏几何求解向量空间角的方法,在计算椭球形颗粒的受力存在一定困难.我们使用空间向量表示光线,通过空间解析几何的方法进行光线追迹,用向量的夹角表示入射光和反射光平面的角度关系,根据光子在界面反射和折射的动量改变,进而在三维方向上计算光子对椭球的作用力[15,16].尽管如此,采用解析几何方法,使用矩阵变换的方式计算折射光、反射光的空间方位角度涉及到多次坐标变换,在后续计算中依然较为复杂[16].
四元数可以很方便地表示空间旋转[17],它在狭义相对论、电磁学、量子力学得到运用[18],目前还广泛用于计算机图形学[19]、飞行器姿态描述、惯性导航领域[20].将四元数旋转引入折射光、反射光空间方位角的计算中,将会简化空间光线追迹的复杂程度.本文介绍如何在RO模型中使用四元数法计算强聚焦光束对椭球微粒的作用力,并通过该模拟方法展示不同形变的椭球形颗粒在光阱中的动力学行为.
2 四元数与旋转
爱尔兰数学家哈密顿(Hamilton)于1843年提出四元数的数学概念,提供了三维空间中运用这种超复数实现坐标变换的方法[17].
2.1 四元数的表示方法
四元数q可用下列超复数形式表达为q=a+bi+cj+dk,其中i,j,k为虚数单位,且满足i2=j2=k2=ijk=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j.若将bi+cj+dk视为向量V=(b,c,d),纯量S=a,则四元数q可表示为q=S+V,还可以写成q=[S,V]这样的形式.
2.2 四元数的运算规则
设有两个四元数分别为q1=[S1,V1],q2=[S2,V2],则两个四元数加法规则满足q1+q2=[S1+S2,V1+V2].若这两个四元数相乘,则

可见四元数相乘的结果还是四元数,它不满足乘法交换律,且不同于四元数的点乘与叉乘的规则.对于四元数q=[S,V]的共轭,满足

四元数q=[S,V]的模为

若一个四元素的模等于1,则该四元数为单位四元数.对于四元数q的逆记为q-1,满足qq-1=1.四元数的逆可由(2)和(3)式求出:

对于单位四元数,它的逆等于其共轭四元数.
2.3 四元数与旋转
三维空间平面Σ上已知点A为(xA,yA,zA),点O′为(xO′,yO′,zO′),图1表示将向量O′A绕点O′旋转角θ到向量O′B.过点O′的Σ面法线方向单位向量u=(xu,yu,zu).用四元数表示向量旋转时,旋转角度满足右手螺旋为正,反之为负.向量O′A=(xA-xO′,yA-yO′,zA-zO′),被旋转向量O′A扩展为只有向量部分的四元数:
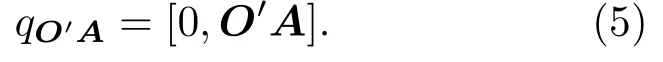
以单位向量u和旋转角度θ构建的旋转轴的四元数为
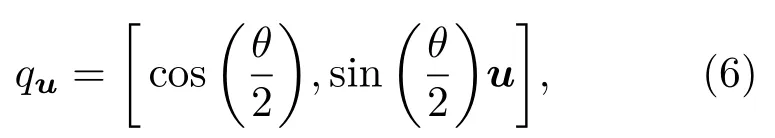
它为单位四元数.向量O′B对应的四元数qO′B满足
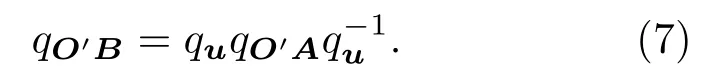
根据(1)—(7)式,计算所得的qO′B的向量部分即为向量O′B.
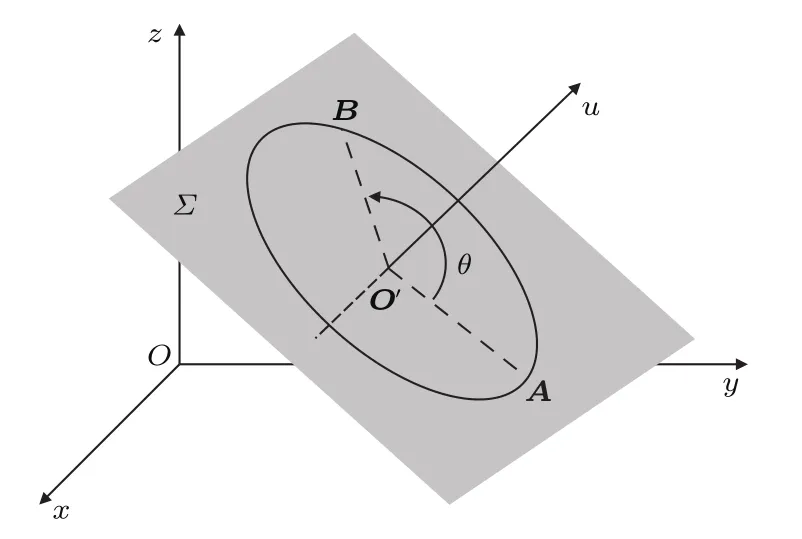
图1 空间平面Σ上O′A以法线u为轴旋转θ角到O′BFig.1.RotatingO′AtoO′Bwith angleθaround the normal axisuin planeΣ.
3 四元数在RO模型中的应用
3.1 运用四元数表示折射和反射光线
在光镊的RO模型中,运用四元数法能追踪入射光线在界面的各种偏折.以光线由光疏介质入射到光密介质为例,如图2所示,界面的法线N取光密介质指向光疏介质为正方向,旋转轴向量v满足

在平面Ω0内以点O为极点,法线N为极轴,以绕向量v按右手螺旋为极角正方向建立平面极坐标系.则L1的极角记为φ1=π+α,L3的极角为φ3=π+β,L2的极角为φ2=2π-α.由L1旋转到L2为φ2-φ1,L1旋转到L3为φ3-φ1.
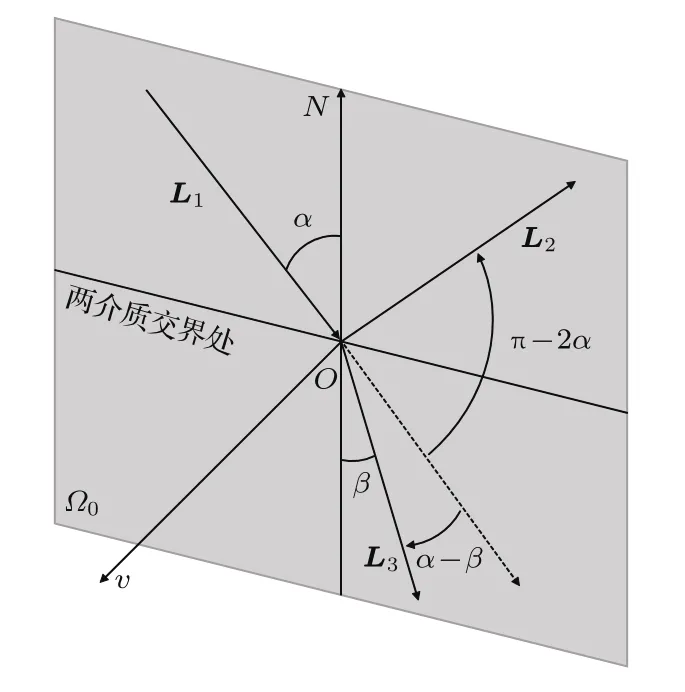
图2 光线在界面的折射和反射示意图Fig.2.Sketch of refractive and reflected lights in the interface.
根据(5)式将L1扩展成四元数qL1=[0,L1],根据(6)式用于旋转到反射光线L2的旋转轴的四元数为

用于旋转到折射光线L3的旋转轴的四元数为
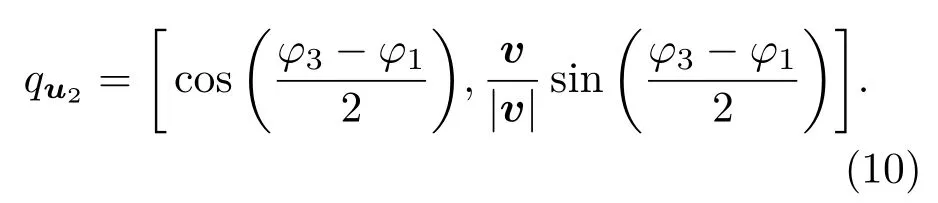
当光线从光密介质进入光疏介质时,同样取光密指向光疏介质的界面法线,旋转轴用(8)式表示.根据右手螺旋确定角度正方向,则旋转轴的四元数依然能用(9)和(10)式表示,则可确定反射光线的四元数qL2与折射光的四元数qL3,进而求得L2和L3的方向向量.根据四元数旋转向量的方法,很方便地计算出光线通过任意界面产生的反射光与折射光向量.
3.2 单根光线对界面折射和反射产生的作用力
当光子经过折射率不同的界面时,光子由于反射和折射导致动量发生改变,从而对界面产生力的作用.光子从光疏介质进入光密介质的界面发生折射和反射,设入射角为α,折射角为β,根据动量守恒,界面受到光子的作用力为[15]

其中R和T为能流Fresnel的反射和透射系数,nm为光线从光源发出传播所在介质的折射率,nr=ns/nm,ns为微粒的折射率,dP为光线的功率元.当光子从光密介质进入光疏介质时,光子对界面的作用力为
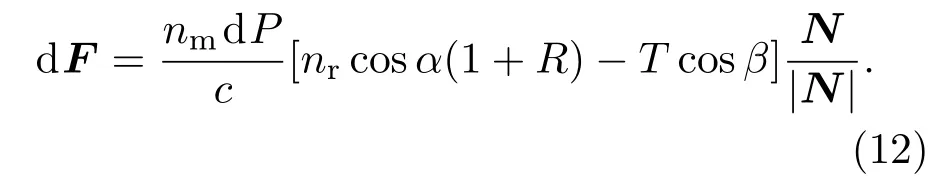
由(11)和(12)式可知微粒所受到的力始终沿着法线,由微粒内部指向外部.我们采用俘获效率Q=Fc/(nmP)表示微粒在光阱中的受力情况.
4 运用四元数法模拟椭球微粒所受的光阱力
由于高斯光束被高数值孔径物镜强聚焦后,束腰在焦平面上且其半径非常小,从物镜后瞳入射面到焦点的光束可近似作为锥形光束传播.物镜后瞳处高斯光束强度分布为I(r)=I0exp(-2r2/ω20),ω0为高斯光束的束腰半径,I0为束腰中心光强,r为光线从后瞳入射点到光轴的距离.在以下计算中,设定高斯光束恰好充满物镜后瞳.
4.1 高斯光束的单根光线追迹
以物镜焦点为坐标原点O,物镜光轴为z轴建立空间直角坐标,椭球微粒中心E位于(xE,yE,zE),如图3所示.ng为玻片折射率,NA为物镜数值孔径.物镜匹配油的折射率与玻璃折射率相近,则物镜焦距fobj=ngRobj/NA.物镜后瞳任意一点H到物镜中心的距离为r,从H点入射的光线经过物镜偏折为IL0指向焦点,且IL0与z轴的夹角为γ1.根据正弦定理sinγ1=r/fobj.当玻片位于z=Zcg处,在玻璃-水界面折射率失配引起的球差作用下,光线在玻璃-水界面上进一步偏折偏离焦点形成IL,IL与z轴交于点Zl,它们的夹角为γ2.σ为O′H与x’轴的夹角,IL=(cosσsinγ2,sinσsinγ2,cosγ2),Zl=Zcg+|Zcg|·tanγ1/tanγ2. 当光线通过玻片之后,光线可看作由Zl点沿IL出射的光线.
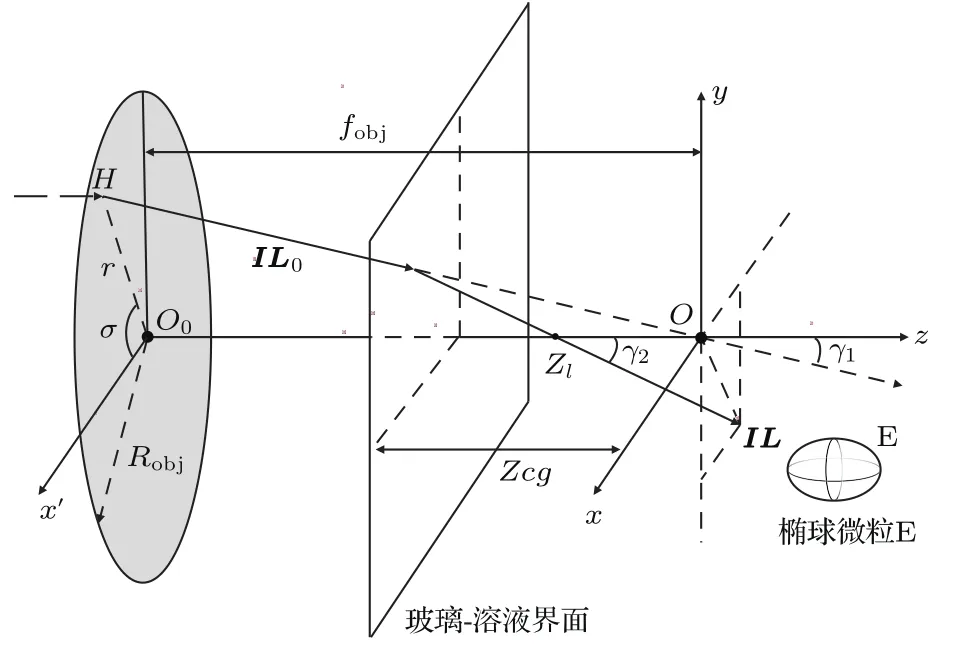
图3 单根光线入射至椭球的光线追迹Fig.3.Tracing a single ray striking an ellipsoidal bead.
设椭球微粒E的方程为
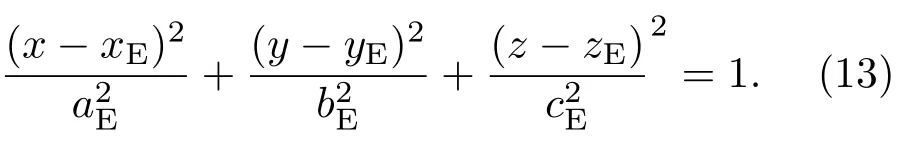
光线IL在椭球微粒E表面反射光线为K0,折射光线为L0,与椭球交于点M0,如图4.在微粒内部,L0在颗粒-溶液界面依次反射Ln,折射为Kn,并依次与颗粒表面相交于Mn,n为自然数.根据(1)—(10)式,由点Mn与Ln-1可计算得出Kn,Ln,其中Mn可由Ln-1直线方程与(13)式联立求解确定[16].
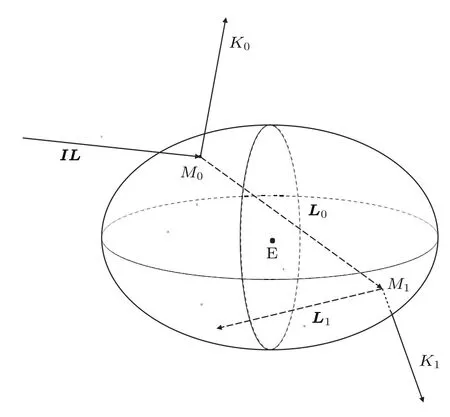
图4 光线在椭球微粒表面的折射和反射Fig.4.Refractive and reflected rays on the interface of an ellipsoidal bead.
根据(11)式和(12)式,光线Ln偏折对微粒的作用力为FIL,n.则该光线对微粒产生的总的作用力为最后再将所有光线对微粒产生的作用力求和,即可得到光束对小球的合力.
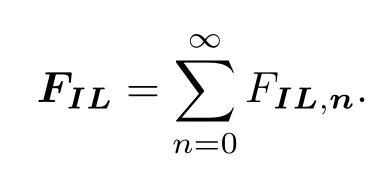
4.2 椭球微粒受到的光阱力
微球所在介质折射率nm=1.33,微球折射率ns=1.59,NA=1.25,Robj=3 mm,ng=1.51,玻片位于Zcg=-10µm处.当aE=bE=cE时,椭球方程退化为球方程,本文中取小球半径rbead=3µm.引入变形系数来描述椭球相对于球体的变形,δx=aE/rbead,δy=bE/rbead,δz=cE/rbead,它们分别表示椭球沿着x,y和z方向的变形.当δx=δy=δz=1时,微粒为半径3µm的球.在球差的影响下,我们采用四元数计算球形微粒的受力曲线Qz和Qx与我们之前空间坐标旋转方法获得的结果一致[16].
图5(a)表示颗粒的横向俘获率.δx=1时微球作为参考曲线,当δx=0.33时小球在z=0处为非稳定状态,一旦小球发生横向偏离便会受到横向的推力加速离开中心位置.对于δx=0.5的微粒,当它横向偏离光阱中心时,微粒所受到的回复力快速增大,并且最大回复力|Qmax|比其他情况更大.从图5(b)中可知,非球形颗粒的轴向稳定性与δx有关.在球差的影响下,δx=0.33的微粒的俘获率曲线与Qz=0没有交点,此时微粒被推离光阱.δx=0.5时微粒受到的最大轴向回复力较δx=1稍小,比δx=2和δx=3的情况稍大.
图5(c)表示轴向变形颗粒的横向俘获率.当颗粒轴向变形拉长时,最大回复力增大.当变形达到一定程度后再拉长颗粒,最大回复力反而变小,如δz=3的微粒比δz=2的微粒受到的光阱力要小.微粒轴向偏离光阱中心时,它所受到的光阱力的曲线如图5(d)所示.微粒轴向变形越大,它在平衡位置时受力曲线斜率为负,且其绝对值越大,表明微粒的轴向稳定性越好.
光阱中颗粒离玻片距离|Zcg|不同时,玻璃-水界面球差对椭球颗粒的轴向俘获效率存在影响.我们计算了不同δz的椭球沿z轴负方向最大俘获效率Qz0,如表1所列.当δz相同时,|Qz0|随着|Zcg|增大而减小.当玻片位置相同时,椭球微粒|Qz0|随δz变化并非单调增大或减小,例如当Zcg=-10,-15或-20µm时,δz=2的椭球微粒的|Qz0|最大,然而当Zcg=-30µm时δz=4的椭球微粒的|Qz0|最大.

图5 (网刊彩色)不同形变椭球微粒的光阱俘获效率 (a)小球沿x方向变形后沿x方向偏离光阱中心时的光阱俘获效率;(b)小球沿x方向变形后沿z方向(光轴方向)偏离光阱中心时的光阱俘获效率;(c)小球沿z方向变形并横向偏离光阱中心时的光阱俘获效率;(d)小球沿z方向变形并轴向偏离平衡位置时的光阱俘获效率Fig.5.(color online)Trapping efficiencyQof an ellipsoidal bead with different deformations:(a)Transverse trapping efficiencyQxfor the bead with deformation ofδx;(b)axial trapping efficiencyQzfor the bead with deformation ofδx;(c)Qxfor the bead with deformation ofδz;(d)Qzfor the bead with deformation ofδz.

表1 玻片位置和轴向变形系数对椭球轴沿z轴负方向最大俘获率的影响Table 1.The maximum negative trapping efficiency affected by different positions of coverslip and axial deformations.

表2 玻片位置和轴向变形系数对椭球轴向平衡位置的影响Table 2.The bead’s equilibrium position affected by different positions of coverslip and axial deformations.
表2展示了玻片不同位置对椭球的轴向平衡位置Zp的影响.当椭球轴向变形系数相同时,椭球微粒轴向平衡位置|Zcg|增大而向负方向偏移,这是因为球差增大,光线通过玻片汇聚的位置朝着负方向移动,从而导致平衡位置随着光线汇聚位置的变化而变化.
4.3 讨 论
四元数能方便地表述空间的旋转.在光线追迹中,对于任意界面光线折射和反射,使用传统欧氏几何的方法求解空间光线的方位角尤为复杂,尤其不适于非球形的颗粒.采用矢量光线追迹,我们可以通过坐标旋转将空间光线的折射和反射简化到入射平面上处理,再通过旋转坐标系的方式回到原坐标系中.目前我们采用四元数法的向量旋转的方式,直接在空间中旋转向量,避免了多次矩阵旋转,简化了光线追迹的困难.
四元数在表述光从光密介质到光疏介质或是光从光疏介质到光密介质时,其公式在表达形式上完全统一,在实际编程计算上更加简洁方便.此外,四元数在光线追迹中不单可以用来求解折射光线与反射光线,还能对目标刚体进行旋转.这意味着可以使用四元数的方式模拟任意摆放的非球形颗粒.
5 结 论
在光镊的RO模型中,追迹光线向量在界面上的反射和折射是计算光阱力的最基本问题.在前人的计算过程中,更多地依赖球形微粒的对称性求解光阱力,本文中提出四元数法旋转入射光向量,可以计算任意界面入射光线的反射光线和折射光线,不依赖微粒的几何特征,比以往的方法适用范围更宽,使得光镊的RO模型的应用面更广泛.
[1]Schnitzer M J,Block S M 1997Nature388 386
[2]Qian H,Chen H,Yan J 2016Acta Phys.Sin.65 188706(in Chinese)[钱辉,陈虎,严洁2016物理学报 65 188706]
[3]Fazal F M,Block S M 2011Nature Photon.5 318
[4]Xia P,Zhou J H,Song X Y,Wu B,Liu X,Li D,Zhang S Y,Wang Z K,Yu H J,Ward T,Zhang J C,Li Y M,Wang X N,Chen Y,Guo Z,Yao X B 2014J.Mol.Cell Biol.6 240
[5]Ouyang H D,Wei M T 2010Annu.Rev.Phys.Chem.61 421
[6]Zhou J H,Ren H L,Cai J,Li Y M 2008Appl.Opt.47 6307
[7]Xu S H,Li Y M,Lou L R 2006Chin.Phys.15 1391
[8]Wright W H,Sonek GJ,Berns M W 1994Appl.Opt.33 1735
[9]Stilgoe A B,Nieminen T A,Knoner G,Heckenberg N R,Rubinsztein-Dunlop H 2008Opt.Express16 15039
[10]Gu Y Q,Gong Z,Lou L R,Li Y M 2007Appl.Laser27 98(in Chinese)[谷勇强,龚錾,楼立人,李银妹 2007应用激光27 98]
[11]Ashkin A 1992Biophys.J.61 569
[12]Fällman E,Axner O 2003Appl.Opt.42 3915
[13]Reihani S N S,Oddershede L B 2007Opt.Lett.32 1998
[14]Sidick E,Collins S D,Knoesen A 1997Appl.Opt.36 6423
[15]Bareil P B,Sheng Y,Chiou A 2006Opt.Express14 12503
[16]Zhou J H,Zhong M C,Wang Z Q,Li Y M 2012Opt.Express20 14928
[17]Kuipers J B 1999Geometry,Intergrability and Quantization(New York:Coral Press)pp127-143
[18]Xu F G 2012Physics with Quaternions(Beijing:Peking University Press)pp16-186(in Chinese)[许方官2012四元数物理学(北京:北京大学出版社)第16—186页]
[19]Pletinckx D 1989Visual Comput.5 2
[20]Zhang R H,Jia H G,Chen T,Zhang Y 2008Opt.Precis.Eng.16 1965(in Chinese)[张荣辉,贾宏光,陈涛,张跃2008光学精密工程16 1965]
PACS:87.80.Cc,42.15.—i DOI:10.7498/aps.66.048701
Using quaternions to analyze the trapping force of an ellipsoidal bead∗
Zhang Shu-He Liang Zhen†Zhou Jin-Hua‡
(Department of Biomedical Engineering,Anhui Medical University,Hefei 230032,China)
3 October 2016;revised manuscript
17 October 2016)
In the ray-optics(RO)model of optical tweezers,tracing refractive and reflected rays with vectors play important roles in calculating the trapping forces.Traditional ray-tracing method with solid geometry,to some extent,is complicated in determining the orientations of those refractive and reflected rays according to spatial incident rays.It is difficult to calculate the trapping forces for irregular particles.In this paper,quaternion is proposed to rotate ray vectors for simplifying the traces of all kinds of spatial rays.Then,it is appropriate to calculate the trapping force of an ellipsoid bead.Based on the algorithm of quaternion and the convention between the interface normal and angular directions,the direction of normal always points from optically denser medium to thinner medium.The rotation axis is the cross product of the incident ray and the interface normal.And the positive angular direction can be determined by right-hand rule based on the orientation of the rotation axis.According to Snell’law,the rotation angle between the incident ray and refractive/reflected ray can be determined.The quaternion for rotation consists of rotation axis and angle.So the refractive and reflected rays are both determined by quaternions of incident ray and rotation based on rotation rules.Furthermore,the force on interface can also be calculated according to momentum changes of the photon before and after the interface refraction and reflection.The quaternion method is used to analyze the effects of coverslip position and deformation ratio on the trapping efficiency of ellipsoid particles.Our simulative results show that the lateral and axial trapping efficiencies are obviously affected by the deformation of the ellipsoid itself.No matter whether the bead deforms transversely or axially,the transverse and axial trapping efficiencies both become larger at a specific deformation.Meantime,the increase of the spherical aberration reduces the maximum axial trapping efficiency,and the equilibrium position of the bead becomes farther away from the center.Using quaternion method,the calculation of refractive lightvector can be simplified in comparison with by using the method of Euclidean geometry or transformation matrix.Theoretically,this quaternion can be used to trace rays on any irregular geometric surfaces.In conclusion,the method of quaternion can make ray tracing easier and extend the applications of RO model.
quaternion,ray tracing,ellipsoidal bead,trapping force
:87.80.Cc,42.15.—i
10.7498/aps.66.048701
∗国家自然科学基金青年基金项目(批准号:31400943)、安徽高校自然科学研究重点项目(批准号:KJ2016A361)和安徽医科大学博士科研资助基金(批准号:XJ201518)资助的课题.
†通信作者.E-mail:liangzhen@foxmail.com
‡通信作者.E-mail:zhoujinhua@ahmu.edu.cn
*Project supported by the Young Scientists Fund of the National Natural Science Foundation of China(Grant No.31400943),the Key Project of Natural Science Foundation of the Anhui Higher Education Institutions,China(Grant No.KJ2016A361),and the Grants for Scientific Research of BSKY from Anhui Medical University,China(Grant No.XJ201518).
†Corresponding author.E-mail:liangzhen@foxmail.com
‡ Corresponding author.E-mail:zhoujinhua@ahmu.edu.cn

