高密度尘埃等离子体的非相干散射理论研究∗

徐彬1李辉2王占阁许正文1吴健

1)(中国电波传播研究所,电波信息环境特性及模化技术国防科技重点实验室,青岛 266107)

2)(哈尔滨工业大学理学院,哈尔滨 150001)

高密度尘埃等离子体的非相干散射理论研究∗

徐彬1)李辉1)2)王占阁1)†许正文1)吴健1)

1)(中国电波传播研究所,电波信息环境特性及模化技术国防科技重点实验室,青岛 266107)

2)(哈尔滨工业大学理学院,哈尔滨 150001)

(2016年9月23日收到;2016年10月28日收到修改稿)

将带电尘埃粒子的影响引入到非相干散射理论中,建立了包含电子、离子和尘埃组分的尘埃等离子体非相干散射理论模型.对火箭喷焰高密度尘埃等离子体条件下,离子谐振区和尘埃谐振区的非相干散射谱线进行了计算,讨论了尘埃粒径、温度和密度对谱线结构的影响,获得了尘埃颗粒影响非相干散射回波特征的基本物理规律.

尘埃等离子体,火箭喷焰,非相干散射理论,尘埃密度

1 引 言

非相干散射雷达是空间环境探测最为理想的地面手段之一.自1958年Gordon[1]将这一理论引入到电离层探测开始,Fejer[2],Dougherty和Farley[3-5],Salpeter[6,7],Hagfors[8]等,分别就磁化、部分电离、不同的电子离子温度比、不同谐振区间的近似解等问题开展了研究,进一步发展了平衡态电离层等离子体非相干散射理论.1969年,Evans[9]发表了综述文章,对热等离子体的Thomson散射理论、非相干散射雷达的脉冲编制技术、等离子参数的提取方法进行了详尽的讨论,至此平衡态的非相干散射理论体系已经基本完备,探测技术也日渐成熟.然而,空间等离子体很多情况下并不满足平衡态的麦克斯韦分布,Sheffield[10]总结和拓展了前人的理论,给出了更一般的情况下,任意粒子分布条件下的非相干散射谱的表达式,这使得非相干散射理论在异常电离层事件分析中有了更广泛的应用.

特定条件下非相干散射理论的发展主要出现在电离层中对流电场和电离层加热两个领域.Raman等[11]利用St-Mauric和Schunk构建的考虑温度的各向异性,热流、黏滞等作用的非麦克斯韦分布理论,建立了电离层中对流电场条件下的非相干散射谱理论模型.Hubert和Lathuillere[12]以及Suvanto[13,14]进一步深化了Raman的研究工作,讨论了更多扰动因素、不同物理模型下功率谱的扰动特征,并提取了非麦克斯韦参数.Gurevich[15]通过使用球函数展开玻尔兹曼方程,最早探讨了低电离层加热条件下的电子的非麦克斯韦分布函数.徐彬等[16,17]给出了非麦克斯韦碰撞等离子体的非相干散射谱的一般表达式,并利用上述分布函数理论分析了其对非相干散射谱的影响,反演了加热电场.电离层加热经常会伴随有人工场向不规则体(artificial field-aligned irregularities,AFAI),Gurevich等[18]推导了基于小尺度温度不规则体的非相干理论,并给出了局部温增的反演方法.电离层加热会引起电子分布函数的高能尾出现,这一现象可以从气辉的观测中得到证实[19,20].综合这两种理论,Xu等[21]给出了包含高能量电子成分的非麦克斯韦非相干散射理论模型,并反演了不规则体的组分参数.

尽管众多学者就不同物理机制的非相干散射理论开展了一系列的研究工作,但特定场景下的非相干散射理论体系还很不完善.一个重要的应用方向是火箭喷焰形成的高密度尘埃等离子体的非相干散射问题.火箭喷焰是由电子、离子、分子以及尘埃粒子组成的弱电离尘埃等离子体,对固体火箭喷焰来说,其主要尘埃成分是Al2O3颗粒,温度在几百到3000开尔文之间,其中分子的浓度远大于电子和离子的浓度,电子与离子的浓度基本相等并远大于Al2O3尘埃粒子的浓度[22].关于尘埃等离子体的介电特性研究,李辉等[23-26]在讨论了带电尘埃粒子造成的附加碰撞形成的电磁波衰减问题,考虑电子和带电尘埃粒子间的弹性库仑碰撞和非弹性碰撞,带电尘埃的引入可以显著改变等离子体的电导率,并增加电磁波的吸收率.上述研究工作回答了非色散介质中的电波传播问题,但尘埃等离子体的非相干散射理论尚未建立.从电子、离子和尘埃三种带电粒子引起的密度扰动出发,本文给出了尘埃等离子体非相干散射理论的一般表达式,并在此基础上对尘埃粒径、温度和密度对非相干散射谱的影响进行了讨论.

2 尘埃等离子体非相干散射理论

尘埃等离子体中包含电子、离子和尘埃三种带电粒子,带电粒子引起的密度扰动可以写为

其中q为带电粒子电量,Q(k,ω)为电荷密度,χ(k,ω)为极化率,k为波矢量,ω为角频率.其中离子引起的密度扰动为

其中Qi为离子产生的全部电荷密度扰动：

这里下标e,i,d分别代表电子、离子和尘埃,ni0为离子密度.其中方程右边第一项为离子的本征扰动,第二项为离子吸引电子引起的扰动,第三项为离子排斥离子引起的扰动,第四项为离子吸引尘埃引起的扰动.因此离子产生的全部电荷密度扰动为

其中ε=1+χe+χi+χd为等离子体的介电函数.则方程(2)可以写为

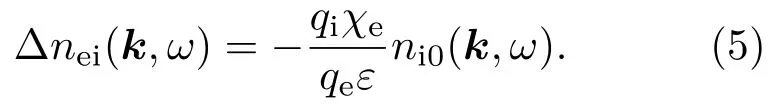
同理,电子引起的扰动为

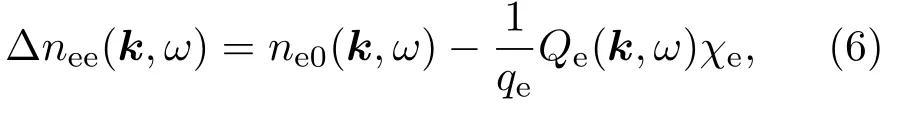
其中ne0为电子密度.电子引起的扰动为自由电子引起的本征扰动和重新排列在电子周围的电子、离子和尘埃引起的扰动的和.因此与电子相关的电荷密度为

与离子相类似,方程右边第一项为电子的本征扰动,第二项为电子排斥电子引起的扰动,第三项为电子吸引离子引起的扰动,第四项为电子排斥尘埃引起的扰动.因此电子产生的全部电荷密度扰动为

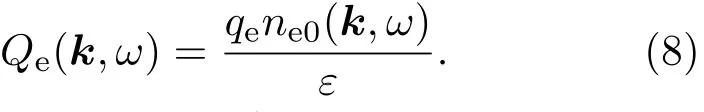
代入(6)式,电子引起的密度扰动为

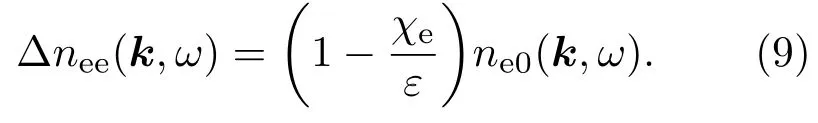
尘埃引起的扰动为

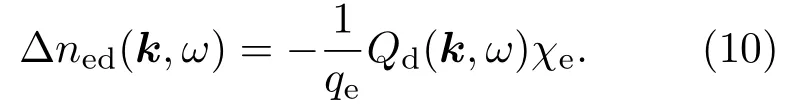
尘埃引起的扰动为尘埃引起的本征扰动和重新排列在尘埃周围的电子、离子和尘埃引起的扰动的和.因此与尘埃相关的电荷密度为

其中nd0为尘埃密度.与离子相类似,方程右边第一项为尘埃的本征扰动,第二项为尘埃排斥电子引起的扰动,第三项为尘埃吸引离子引起的扰动,第四项为尘埃排斥尘埃引起的扰动.因此尘埃产生的全部电荷密度扰动为

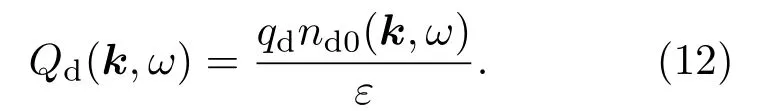
代入(10)式,尘埃引起的密度扰动为

因此单个粒子的扰动功率谱为

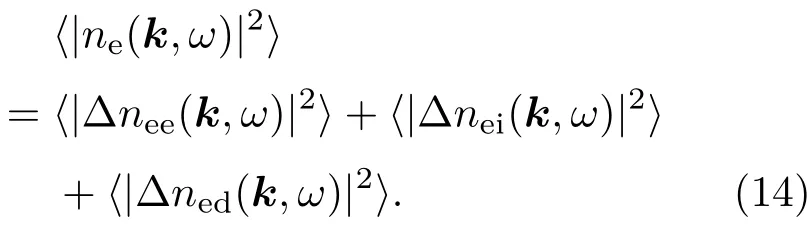
对存在速度分布的粒子系统来说,功率谱为

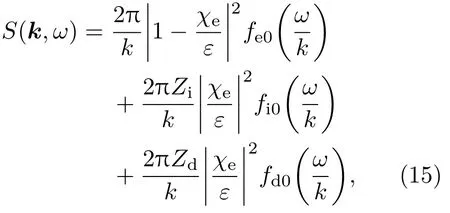
其中Zi和Zd为离子电荷数和尘埃电荷数;fe0,fi0和fd0分别为电子、离子和尘埃的速度分布函数.对麦克斯韦分布有

这里v为速度,vth为热速度.电子、离子和尘埃的极化率为

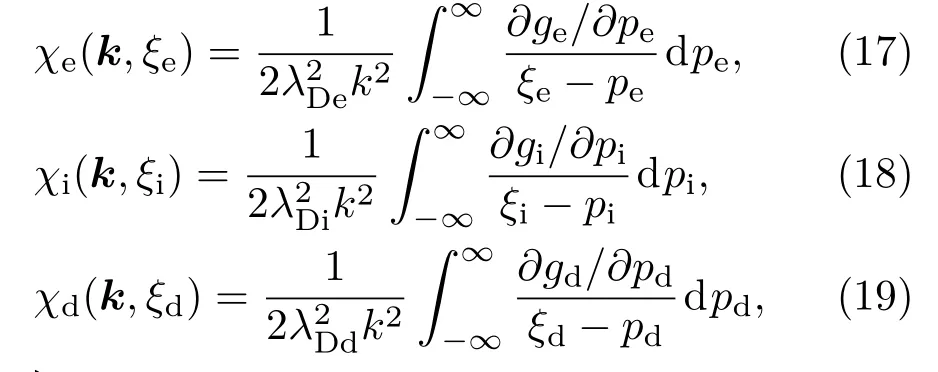
其中pe=v/vthe,pi=v/vthi,pd=v/vthd,ξe=ω/kvthe,ξi=ω/kvthi和ξd=ω/kvthd,vthe,vthi和vthd分别为电子、离子和尘埃的的热速度;λDe,λDi和λDd分别为电子、离子和尘埃的德拜长度;ge,gi和gd为电子、离子和尘埃的归一化分布函数.

对麦克斯韦分布有：

其中Te,Ti和Td分别为电子、离子和尘埃的温度.将(16)式,(20)—(22)式代入(15)式即可计算包含尘埃粒子的非相干散射谱.

3 高密度尘埃等离子体非相干散射谱数值模拟

使用上面的尘埃等离子非相干散射理论,我们对典型的火箭喷焰形成的高密度尘埃等离子体的非相干散射谱进行了计算.其中电子密度为1018m-3,电子温度为2000 K,尘埃密度为1013m-3,尘埃半径为0.1µm.计算中由于尘埃极化率计算存在溢出现象,对尘埃极化率计算公式做如下调整：

图1—图3给出了不同尘埃粒径、温度和密度条件下的非相干散射谱的计算结果.由于非相干散射谱包含电子项、离子项和尘埃项三个部分的贡献,因此对应的非相干散射谱存在电子谐振区、离子谐振区和尘埃谐振区三个谱线区间,其中前两者通常称为等离子体线和离子线.由于尘埃带电成分的引入,我们可以称尘埃谐振区的谱线为尘埃线.由于尘埃粒子的质量很大,其对高频段的电子谐振区的贡献很小,等离子体线的谱线特征主要由电子特征参数决定,因此我们没有给出电子谐振区的计算结果.

在离子谐振区和尘埃谐振区,尘埃的影响显著.从图1(a)可以看到,尘埃谐振区非相干散射谱呈现为单峰结构,随尘埃粒径的增加谱宽变窄,幅度增加,或者说在保持谱线面积近似相等的条件下,粒径参数主要控制谱线的尖锐程度.从图1(b)可以看到,在离子谐振区,非相干散射谱呈现更为典型的双峰结构,随粒径增加,谐振谱线间距变小,上下行离子线谱本身的谱宽变窄,非相干散射谱逐渐从有一定分布的谱线结构转变为单一的谐振线.

尘埃温度的影响刚好相反.从图2可以看到,随温度的增加,尘埃谐振区谱宽变宽,离子谐振区同时出现谱宽变宽和上下行谱线间间距变大.从图3可以看到,随尘埃密度的增大,尘埃谐振区谱线宽度变化不大,但谱线幅度或谱线面积增加.在离子谐振区,随尘埃密度的增加功率谱幅度增加,谱宽和谱线间距变小.

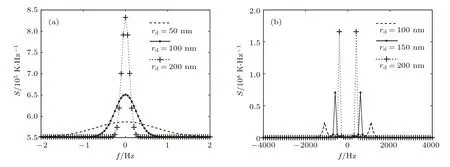
图1 尘埃粒径对非相干散射谱的影响 (a)尘埃谐振区;(b)离子谐振区Fig.1.The effect of dust radius on incoherent scatter spectra：(a)Dust resonance region;(b)ion resonance region.

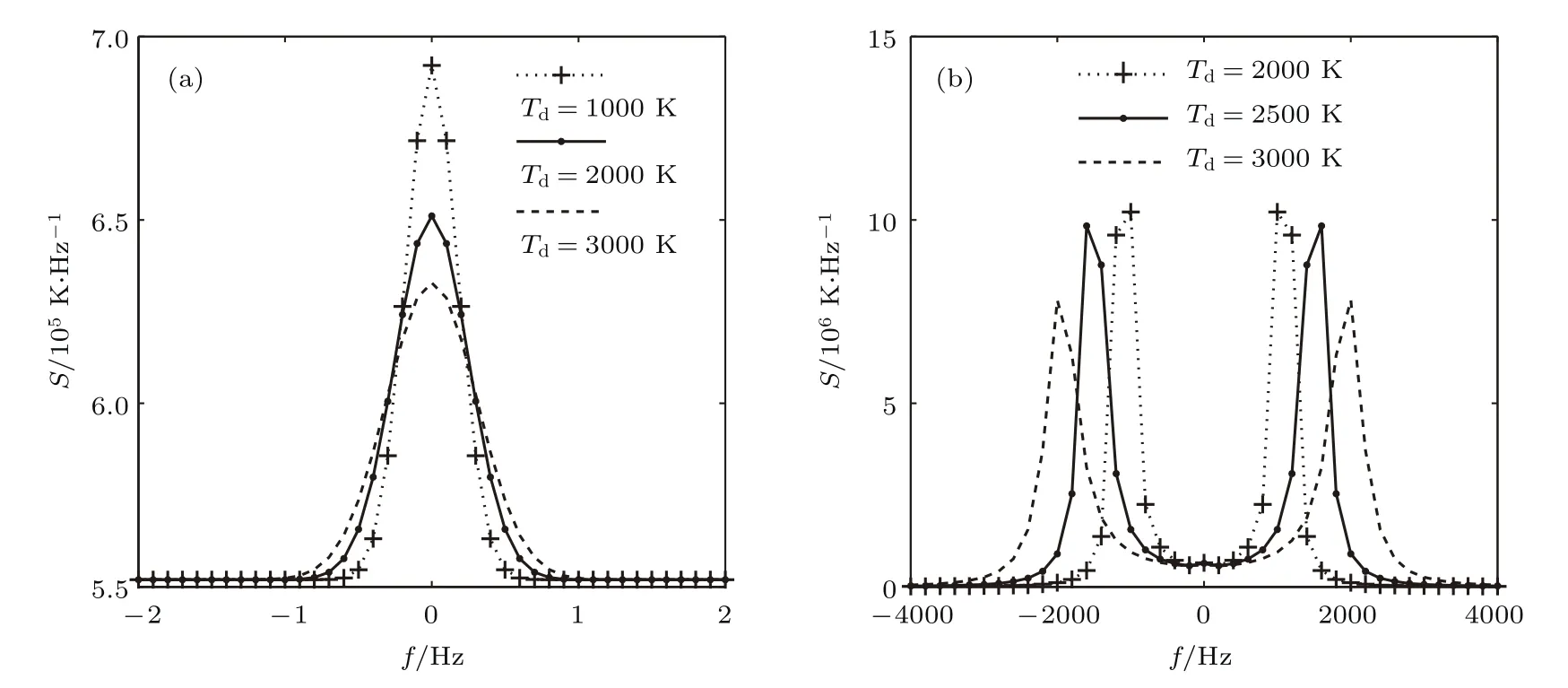
图2 尘埃温度对非相干散射谱的影响 (a)尘埃谐振区;(b)离子谐振区Fig.2.The effect of dust temperature on incoherent scatter spectra：(a)Dust resonance region;(b)ion resonance region.

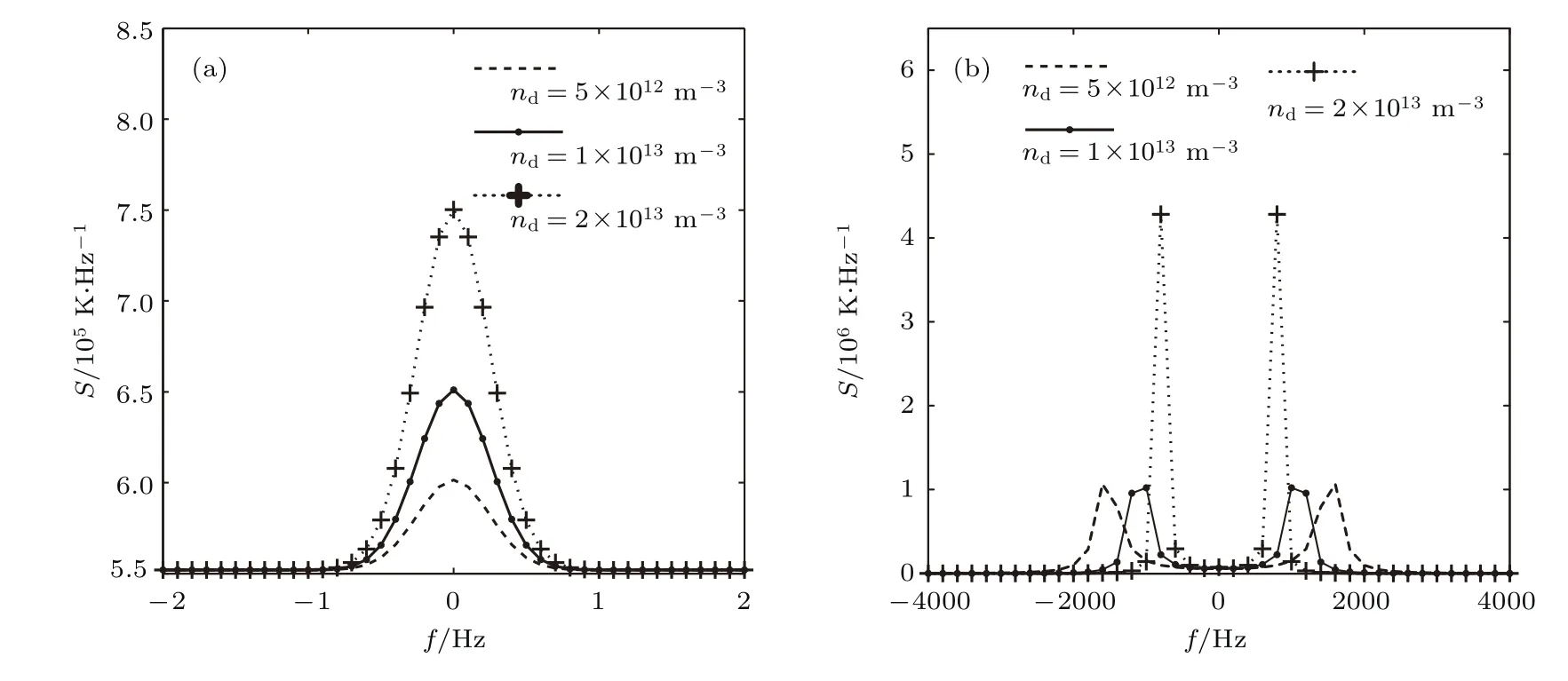
图3 尘埃密度对非相干散射谱的影响 (a)尘埃谐振区;(b)离子谐振区Fig.3.The effect of dust density on incoherent scatter spectra：(a)Dust resonance region;(b)ion resonance region.

从谱线变化特性对应的物理机制来看,在尘埃谐振区,尘埃的控制机制与离子对离子线谱的控制机制基本类似,均为随粒径(质量)增大和温度降低,谱宽变窄,随密度增高,幅度和面积增大,这好像带电尘埃是一个“重”离子,从物理原理上说,这是合理的.但在离子谐振区,尘埃的控制机制则完全不同：一方面带电尘埃在该区间不再是“主控因素”,或者说不再是直接控制因素,其角色由离子扮演,而尘埃通过吸附离子的方式影响离子线谱,因此随尘埃密度的增大,离子线谱并不呈现面积增大的特征(该特征与离子密度直接相关);另一方面,尘埃密度通过调整德拜半径或静电屏蔽球的大小来控制离子,使得其对离子线谱的影响极为显著.我们对比尘埃影响的离子线和相同参数条件下不包含尘埃的离子线可以发现,尘埃离子线的幅度远大于后者,且受尘埃束缚,离子线的谐振频率存在很大的变化.这些影响包括两面：一方面由于相对高密度的尘埃粒子的引入,可以增强离子线谱,使得我们可以更容易地观测到火箭喷焰的非相干散射现象;另一方面,由于尘埃对离子线谱频率和幅度的显著改变,使得原有的基于传统非相干散射理论体系建立的反演方法无法有效地反演喷焰等离子体的相关参数,会造成反演参数量级上的误差,这在利用非相干散射原理开展的尘埃等离子体探测试验中,必须予以慎重考虑.

4 结 论

非相干散射雷达一直是最为主要的空间等离子体地面探测手段,但由于自然的空间尘埃等离子体中的尘埃密度较低(如极区夏季中层回波PMSE[27]),带电尘埃对非相干散射谱的贡献可以完全忽略,因此一直未出现尘埃等离子体的非相干散射理论.在固体火箭尾焰中,推进剂燃烧可以形成大量的Al2O3纳米级和微米级的尘埃颗粒,且燃烧形成的高温电离产生了极高的电子密度,这些因素使得高密度带电尘埃的贡献变得十分显著.因此我们发展了尘埃等离子的非相干散射理论,以便对火箭喷焰等高密度尘埃等离子体的非相干散射特征进行准确的计算.文中给出了包含电子、离子和尘埃的尘埃等离子体非相干散射谱的计算公式,并对离子谐振区和尘埃谐振区的非相干散射谱线进行了计算,讨论了尘埃粒径、温度和密度对谱线结构的影响,获得了尘埃颗粒影响非相干散射回波特征的基本物理规律.尽管如此,使用单一的尘埃粒径参数来描述尘埃等离子体的非相干散射特性是不够精确的,考虑实际的尘埃粒子尺寸分布特征,建立相应的理论模型,并与试验进行对比是我们下一步所要完成的工作.

[1]Gordon W E 1958Proc.IRE46 1824

[2]Fejer J A 1960Can.J.Phys.38 1114

[3]Dougherty J P,Farley D T 1960Proc.Roy.Soc.London A259 79

[4]Dougherty J P,Farley D T 1963J.Geophys.Res.68 5473

[5]Dougherty J P,Farley D T 1966J.Geophys.Res.71 4091

[6]Salpeter E E 1960Phys.Rev.120 1528

[7]Salpeter E E 1961Phys.Rev.122 1663

[8]Hagfors T 1961J.Geophys.Res.66 1699

[9]Evans J V 1969Proc.IEEE57 496

[10]Sheffield J 1975Plasma Scattering of Electromagnetic Radiation(New York：Academic Press)pp113-128

[11]Raman R S,St-Maurice J P,Ong R S B 1981J.Geophys.Res.86 4751

[12]Hubert D,Lathuillere C 1989J.Geophys.Res.94 3653

[13]Suvanto K 1988Radio Sci.23 989

[14]Suvanto K 1990Plan.Space Sci.38 903

[15]Gurevich A V 1978Nonlinear Phenomena in the Ionosphere(Berlin：Springer-Verlag)pp58-82

[16]Xu B,Wu Z S,Wu J,Xue K 2009Acta Phys.Sin.58 736(in Chinese)[徐彬,吴振森,吴健,薛昆2009物理学报58 736]

[17]Xu B,Wu Z S,Wu J,Xue K 2009Sci.China E52 1112

[18]Gurevich A V,Hagfors T,Carlson H,Lukyanov A V,Zybin K P 1998Phy.Lett.A246 335

[19]Gustavsson B 2005Ann.Geophys.23 1747

[20]Mishin E,Carlson H C,Hagfors T 2000Geophys.Res.Lett.27 2857

[21]Xu B,Wang Z G,Xue K,Wu J,Wu Z S,Wu J,Yan Y B 2010J.Atmos.Sol.Terr.Phys.72 492

[22]Shi Y X 2008Ph.D.Dissertation(Xi’an：Xidian University)(in Chinese)[石雁祥 2008博士学位论文(西安：西安电子科技大学)]

[23]Li H,Wu J,Zhou Z X,Yuan C X 2016Phys.Plasma23 073702

[24]Li H,Wu J,Zhou Z X,Yuan C X,Jia J S 2016Phys.Plasma23 073301

[25]Li H,Wu J,Zhou Z X,Yuan C X 2016Phys.Lett.A380 2540

[26]Li H,Wu J,Zhou Z X 2016Ann.Geophys.34 117

[27]Rapp M,Lübken F J 2004Atmos.Chem.Phys.4 2601

PACS:94.05.Bf,94.05.Jq,94.20.Fg,94.20.Tt DOI:10.7498/aps.66.049401

Study on incoherent scatter theory of high density dusty plasma∗

Xu Bin1)Li Hui1)2)Wang Zhan-Ge1)†Xu Zheng-Wen1)Wu Jian1)
1)(National Key Laboratory of Electromagnetic Environment,China Research Institute of Radio Wave Propagation,Qingdao 266107,China)
2)(Department of Physics,Harbin Institute of Technology,Harbin 150001,China)

23 September 2016;revised manuscript

28 October 2016)

Incoherent scatter radar is one of the most important detection instruments of the space plasma.But because of the low dust density in natural space plasma,the contribution of charged dust to incoherent scatter spectrum can be completely ignored,therefore the incoherent scattering theory has not appeared in dusty plasma.In the solid rocket plume,the propellant combustion can form a large number of nanometer-and micronmeter-sized dusty particles,and produce a high electron density from high temperature ionization,which makes considerable contributionto charged dusty particles with the high density.Therefore,we develop the incoherent scattering theory of dusty plasma in order to calculate the scattering characteristics of high density dusty plasma produced by rocket plume,for example.The theoretical model including electrons,ions and dusty particles is established by combining effects of charged dusty particles.The incoherent scatter spectral lines of ion resonance region and dust resonance regionare calculated.The effects of dusty particle radius,temperature and density on spectral line structure are discussed.With the increases of dusty particle radius and density,the amplitude of power spectrum increases.With the increase of dust temperature,the amplitude of power spectrum decreases.In the dust resonance region,the control mechanism of dust in spectrum is similar to that of the ions.With the increase of particle size(mass)and decrease of the temperature,the spectrum width narrows,and amplitude and area increase with the increase of density.But in the ion resonance region,the dust control mechanism is completely different,and the influence of the dust on ion line is in the way of attracting ions.So with the increase of dust density,ion line characteristics do not show that the area increases,and dust controls ions by adjusting the Debye radius or electrostatic shielding ball size.By comparing the ion lines with and without dust under the same parameters conditions,the amplitude of the ion line with dust is much larger than that without dust,and the resonance frequency of the ion line is greatly changed.With the dust particles of a relatively high density,one can enhance the ion line,hence the incoherent scattering phenomenon can be more easily observed in rocket plume.On the other hand,due to significant changes of frequency and amplitude in the ion line spectrum,the incoherent scattering inversion method based on the traditional theory will cause a large error in the inversion parameter,even a failure of parameter retrieval.The incoherent scattering theory and relevant physical laws of dusty plasma are presented,which are of great significance for establishing the incoherent scattering theory system and studying the rocket plume parameters.

dusty plasma,rocket plume,incoherent scatter theory,dusty particle density

:94.05.Bf,94.05.Jq,94.20.Fg,94.20.Tt

10.7498/aps.66.049401

∗国家自然科学基金(批准号：41004065,41104108,61601419,11672068)和电波环境特性及模化技术国防重点实验室基金资助的课题.

†通信作者.E-mail：xiaogezi2@126.com

*Project supported by the National Natural Science Foundation of China(Grant Nos.41004065,41104108,61601419,11672068)and the National Key Laboratory of Electromagnetic Environment,China.

†Corresponding author.E-mail：xiaogezi2@126.com