空气中一维声栅对微粒的声操控∗

黄先玉 蔡飞燕李文成 郑海荣 何兆剑 邓科赵鹤平

1)(吉首大学物理与机电工程学院,吉首 416000)

2)(中国科学院深圳先进技术研究院,劳特伯生物医学成像中心,深圳 518055)

空气中一维声栅对微粒的声操控∗

黄先玉1)2)蔡飞燕2)†李文成1)郑海荣2)何兆剑1)邓科1)‡赵鹤平1)

1)(吉首大学物理与机电工程学院,吉首 416000)

2)(中国科学院深圳先进技术研究院,劳特伯生物医学成像中心,深圳 518055)

(2016年9月26日收到;2016年11月22日收到修改稿)

本文对一维空气声栅表面微粒受到的声辐射力进行了详细的理论研究.首先采用有限元方法研究一维声栅的透射性质及表面声场分布,然后将有限元与动量张量积分结合研究处于一维声栅表面微粒受到的声辐射力特征.声栅共振透射增强是表面周期衍射波与狭缝Fabry-Perot共振耦合形成的,并且与声栅周期和厚度密切相关.研究发现,当共振波长与声栅周期相当时,微粒在其表面可受到指向声栅板面的声吸引力;当共振波长为声栅周期的二倍及以上,微粒可受到指向狭缝中的吸引力,且强度远小于第一种情况的吸引力.因此,在声栅处于共振波长与周期相当的共振模式时,可以在空气中利用声栅表面操控、吸引和排列微粒.

声操控,声辐射力,微粒俘获,一维声栅

1 引 言

声操控主要是利用超声分类、筛选、移动微粒等,是声波力学效应的一个重要用途之一[1,2].其主要物理原理是由于声波携带动量和能量,处于声场中的物体对声波散射、吸收,从而与声场发生动量和能量交换,导致物体受到声辐射力的作用[3,4].声操控作为一种非接触的操控微粒方式具有很多优点,如声波产生装置简单、声波穿透性良好可以操控非透明介质中的微粒,此外千赫兹的超声在空气中还可以操控毫米甚至是厘米尺寸的微粒.传统声操控的入射声场一般由单换能器或者换能器阵列产生,如利用单换能器产生的聚焦声场、平面波声场,利用换能器阵列产生的驻波场、多种形态的声场分布等[5],均实现了各种操控现象.但是单换能器制备完成后声场形态很难调控,换能器阵列声场形态可通过电子延迟进行调控,但研制工艺要求高,造价十分昂贵.因此,需要研究新的手段产生优化声场实现微粒的多种形式的操控.

声子晶体、声超常材料等[6-13]人工结构可以灵活调控声波的传播及声场分布,这为声操控的优化声场提供了有效的手段.已有很多研究者利用声子晶体在水中调控的声场来改变微粒受到的声辐射力的大小与方向,实现微粒的灵活操控.如,Wang等[14,15]利用含周期孔的声子晶体板结构中的局域强场实现了粒子的排列,随后他们利用一维三组元声子晶体结构产生的可控空间局域强场,实现了微粒的俘获与输运;Qiu等[16]通过激发含栅格的双板结构中的兰姆波获得局域强场,在板间实现增强的声吸引力和排斥力;最近,Lu等[17]通过激发含斜栅的双板中兰姆波获得局域强场,也实现了增强的声吸引力和排斥力;此外,我们小组也研究了水中微粒在声子晶体板表面受到的反常声辐射力的产生机理及筛选应用[18-20].

本文研究空气中微粒在一维声栅表面受到的声辐射力的分布和特征.我们首先采用有限元方法研究一维声栅的透射性质及表面声场分布,然后将有限元与动量张量积分结合研究处于一维声栅表面微粒受到的声辐射力特征,并重点研究在声栅产生两个不同共振模式时微粒分别在其表面受到的声辐射力分布.结果表明,当共振波长与声栅周期相当时,微粒在其表面可受到指向声栅板面的声吸引力;当共振波长为声栅周期的二倍及以上,微粒可受到指向狭缝中的吸引力,且强度远小于第一种情况的吸引力.因此,在声栅处于共振波长与周期相当的共振模式时,可以在空气中利用声栅表面操控、吸引和排列微粒.

2 原理与结果

2.1 一维声栅透射性质及声场特征

图1(a)表示的是一维声栅操控微粒的示意图.该声栅是由一块厚度t=6.25 mm的钢板放置在空气中,以晶格常数d=8.34 mm,周期性切割宽w=1 mm的狭缝组成.一个圆柱状半径R=0.04d的聚苯乙烯(polystyrene,PS)泡沫微粒放置在声栅表面上,微柱底部距离栅上表面的垂直距离为ΔY,粒子中心距离系统中心轴的水平距离为ΔX.材料的声学参数如下：空气纵波速度为cl=340 m/s,密度ρ=1.29 kg/m3;聚苯乙烯泡沫[21]纵波速度为cl=820 m/s,横波速度为ct=550 m/s,密度为ρ=100 kg/m3;钢纵波速度为cl=6010 m/s,横波速度为ct=3320 m/s,密度为ρ=7760 kg/m3.我们采用有限元的COMSOL Multiphysics软件进行数值仿真[22].在仿真计算中,四周采用平面波辐射边界条件来减小反射波对计算的影响.如果没有特别说明,我们取ΔX=0.25d和ΔY=0.05d,入射声场为沿Y方向传播的平面波,声压为2 kPa.

图1 系统示意图与归一化透射谱及无量纲Y方向声辐射力 (a)系统的示意图,微柱(蓝色)放在一维声栅表面;(b)平面波正入射一维声栅的透射谱(黑色虚线),有结构时,无量纲Y方向声辐射力函数(Yy黑色实线),入射声场垂直于栅格表面沿正Y方向Fig.1.Schematic view of a 1D grating,transmission and dimensionlessY-directional acoustic radiation force(ARF)function：(a)Schematic view of a 1D grating,a cylindrical particle(blue)is placed on the top of this grating;(b)the transmission(black solid line)and dimensionlessY-directional acoustic radiation force(ARF)function(black dash line)representing the force exerted on the cylindrical particle for the system employing a planar wave at normal incidence to the bottom of the grating.

声栅的透射性质如图1(b)中黑色的虚线所示,透射谱中有两个显著的透射峰,其对应的频率为22.7,39.6 kHz.此外,我们进一步研究了两个共振透射频率处系统的压力场分布,如图2所示.图2(a)是共振频率峰22.7 kHz的压力场,可以看出,能量大部分局域在缝里.图2(b)是共振频率为39.6 kHz的压力场,可以看出能量除了局域在狭缝里,还有一部分能量局域在栅表面.根据已有研究及压力场分布[23,24],共振透射增强峰是由表面衍射波和周期缝里Fabry-Perot(FP)共振耦合引起的.进一步分析发现第一个共振模式和第二个共振模式的波长与栅格厚度关系分别为2.39t和1.37t,与栅格周期关系分别为1.8d和1.03d.从图2声场分布可以发现,当第一个共振模式的波长为声栅周期的二倍时,该模式在周期方向仅存在一个能量极值点,由于与狭缝波导共振耦合的作用,其在狭缝表面;当第二个共振模式的波长与声栅周期相当时,在栅格表面一个周期内,该模式在周期方向存在两个能量极值点,分别在狭缝表面和两个栅格之间的中心表面;且声场在声栅表面局域程度远大于第一个共振模式.

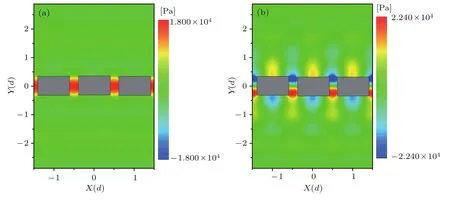
图2 (网刊彩色)一维声栅周围空气声压场分布 (a)共振频率为22.7 kHz;(b)共振频率为39.6 kHzFig.2.(color online)Distribution of pressure field in air：(a)For the frequency 22.7 kHz;(b)for the frequency 39.6 kHz.

2.2 微粒在一维声栅表面的声辐射力特征

我们采用有限元与动量张量积分结合的方法研究微粒在声栅表面受到的声辐射力[25,26],其表达式如下：

其中积分区域dA=ndA,n表示单位力,沿着粒子半径的方向向外;A表示在平衡状态时仅包裹粒子的任意表面.〈S〉为含时平均动量张量,其表达式如下：

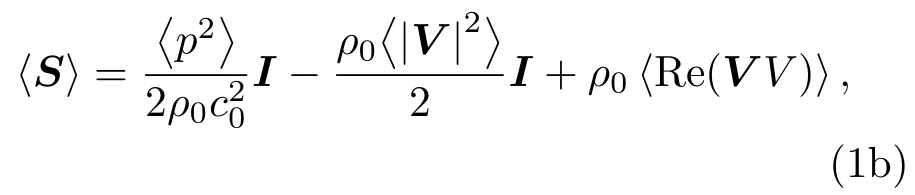
其中V和p分别表示速度场和压力场,ρ0和c0表示基底的密度和声速,I表示单位张量.无量纲声辐射力：Yx(y)=Fx(y)/I0可以用来表示粒子所受声辐射力的相对大小,其中I0表示的是没有粒子时,通过粒子原来所在位置的能量密度.根据(1a)和(1b)式我们可知二维的声辐射力Fx与Fy的表达式[27]：

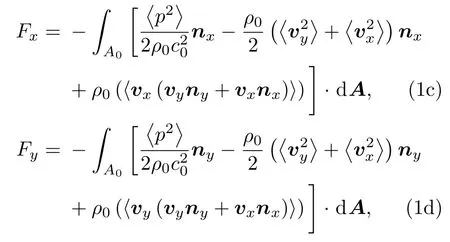
其中nx(y)表示X与Y方向的单位矢量,vx(y)表示X与Y方向的速度分量.

图1(b)展示了粒子在ΔX=0.25d和ΔY=0.05d处所受的声辐射力,黑色实线表示微粒在Y方向无量纲的声辐射力.从图中可以看出,在22.7 kHz和39.6 kHz这两个共振峰频率下,微柱在Y方向所受的声辐射力是负值;在其他频率段,微粒受到的声辐射力为正值且很小;此外,在39.6 kHz共振频率下,其负声辐射力的强度远大于在22.7 kHz共振频率时的声辐射力.其主要原因是由于在频率为39.6 kHz时,系统处于表面衍射波与周期狭缝二阶FP共振耦合模式,其声场能量局域在声栅板表面,而在频率为22.7 kHz时,系统处于表面衍射波与周期狭缝一阶FP共振耦合模式,其声场能量主要局域在狭缝中.

为了进一步获得微粒在一维声栅表面的受力特征,我们分别研究了共振频率为22.7 kHz(图3(a))和39.6 kHz(图3(b))时聚苯乙烯泡沫微柱在声栅表面受到的声辐射力空间分布,其中箭头表示微柱所受声辐射力的方向,颜色表示微柱所受声辐射力的幅值.微柱位置在X方向的变化ΔX是由-1.1d到1.1d,在Y方向的变化是ΔY由0.05d到1.1d.从声辐射力的强度来看,22.7 kHz共振频率处的空间极值声辐射力远小于39.6 kHz共振频率处的空间极值声辐射力;且22.7 kHz共振频率处声辐射力的极大值在一个周期范围内仅有一处在狭缝表面,而39.6 kHz共振频率处声辐射力的极大值在一个周期范围内有两处,分别在声栅表面离狭缝约d/4和3d/4.从声辐射力的方向来看,当ΔY＞0.5d时,22.7 kHz和39.6 kHz共振频率处的Y方向声辐射力均指向Y轴正方向,且强度较小;当ΔY＜0.5d时,两个共振频率处的Y方向声辐射力在大部分位置指向Y轴负方向,且强度随着微柱Y轴坐标靠近狭缝(22.7 kHz)或靠近声栅表面离狭缝约d/4和3d/4(39.6 kHz),Y方向声辐射力逐渐增大.X方向声辐射力在22.7 kHz一个栅格周期内拥有两个零点位置,分别在狭缝中间和声栅表面中间;在39.6 kHz一个栅格周期内拥有四个零点位置,分别在狭缝中间,离狭缝d/4,d/2,3d/4处.

对于22.7 kHz和39.6 kHz微粒受到的声辐射力空间分布特征的物理机理可解释如下：根据图2(a)和图2(b)的声压场分布,在第一个共振模式(图2(a)),由于共振波长约为声栅周期的二倍,声场主要局域在狭缝中,狭缝出口略有局域强场,而栅格表面几乎无局域声场;在第二个共振模式(图2(b)),由于共振波长与声栅周期相当,声场一方面局域在狭缝中,另一方面在声栅表面中心位置具有声场能量极大值,在狭缝中具有声场能量极小值,因此第二个共振模式在声栅表面声场局域(梯度)分布更明显.微粒在声场中受到的声辐射力可分为散射力和梯度力,当微粒在非梯度声场中,其主要受到散射力的作用,声辐射力方向一般指向波传播方向;当微粒在梯度声场中,其主要受到梯度力作用,声辐射力方向一般指向声场强度极值(极大或极小)方向.在本系统中,当微柱远离声栅表面,其受到的主要是散射场的作用,该场对微粒产生的是散射力,指向波传播的方向,即微粒受到的力为正;当微粒靠近声栅表面,一方面,微粒受到散射场作用,获得的散射力指向波传播方向,另一方面,微粒还受到声栅表面共振耦合产生的梯度场的作用,该场对微粒产生的是梯度力,指向声场极强的位置,此时,微柱所受的总声辐射力是梯度力和散射力竞争的结果,即：当梯度力占主导作用时,微柱所受的力为负力,反之为正[18];因此,越靠近板表面,微粒受到的梯度场越大,相应的声辐射力负值越大.此外,在39.6 kHz时,微粒在声栅表面受到的X方向声辐射力极小值为声压场极小位置,因此在声栅一个周期表面内具有两个微粒停驻位置.

图3 (网刊彩色)微柱的位置变化在X方向ΔX从-1.1d到1.1d以及Y方向ΔY从0.05d到1.1d,半径为0.04d的PS泡沫微柱所受的力空间分布图 (a)频率为22.7 kHz;(b)频率为39.6 kHz;钢栅用图中灰色的矩形块来表示Fig.3.(color online)Total radiation force map exerted on a PS foam cylindrical particle withR=0.04don the top side of the grating with its position ΔXfrom-1.1dto 1.1d,ΔYfrom 0.05dto 1.1d：(a)For the frequency 22.7 kHz;(b)for the frequency 39.6 kHz;Gray rectangle representing the position of 1D steel grating.

3 结 论

我们详细研究了声栅共振时微粒在其表面受到的声辐射力.结果表明当共振波长与声栅周期相当时,微粒在其表面可受到指向声栅板面的声吸引力;当共振波长为声栅周期的二倍及以上,微粒可受到指向狭缝中的吸引力,且强度远小于第一种情况的吸引力.因此,在声栅处于共振波长与周期相当的共振模式时,可以在空气中利用声栅表面操控、吸引和排列微粒.

参考文献

[1]Liu Y Y,Hu J H 2009J.Appl.Phys.106 034903

[2]Shi J J,Ahmed D,Mao X L,Lin S,Lawit A,Huang T J 2009Lab Chip9 2890

[3]Borgnis F E 1953Rev.Mod.Phys.25 653

[4]Hasegawa T,Hino Y,Annou A,Noda H,Kato M,Inoue N 1993J.Acoust.Soc.Am.93 154

[5]Marzo A,Seah S A,W.Drinkwater B,Sahoo D R,Long B,Subramanian S 2015Nat.Commun.6 8661

[6]Wang J W,Cheng Y,Liu X J 2014Chin.Phys.B23 054301

[7]Wang J W,Yuan B G,Cheng Y,Liu X J 2015Sci.China:Phys.Mech.Astron.58 024302

[8]Li Y,Liang B,Xu T,Zhu X F,Zou X Y,Cheng J C 2012Appl.Phys.Lett.101 233508

[9]Li Y,Liang B,Zou X Y,Cheng J C 2012Chin.Phys.Lett.29 114301

[10]Liu Z Q,Zhang H,Zhang S Y,Fan L 2014Appl.Phys.Lett.105 053501

[11]Wang Y R,Zhang H,Zhang S Y,Fan L,Sun H X 2012J.Acoust.Soc.Am.131 EL150

[12]Zhu X F,Liang B,Kan W W,Zou X Y,Cheng J C 2011Phys.Rev.Lett.106 014301

[13]Zhu X F,Li K,Zhang P,Zhu J,Zhang J T,Tian C,Liu S C 2016Nat.Commun.7 11731

[14]Wang T,Ke M Z,Xu S J,Feng J H,Qiu C Y,Liu Z Y 2015Appl.Phys.Lett.106 163504

[15]Wang T,Ke M Z,Qiu C Y,Liu Z Y 2016J.Appl.Phys.119 214502

[16]Qiu C Y,Xu S J,Ke M Z,Liu Z Y 2014Phys.Rev.B90 094109

[17]Lu S F,Zhang X,Wu F G,Yao Y W,Chen Z W 2016J.Appl.Phys.120 045102

[18]Cai F Y,He Z J,Liu Z Y,Meng L,Cheng X,Zheng H R 2011Appl.Phys.Lett.99 253505

[19]Li F,Cai F Y,Liu Z Y,Meng L,Qian M,Wang C,Cheng Q,Qian M L,Liu X,Wu J R,Li J Y,Zheng H R 2014Phys.Rev.Appl.1 051001

[20]He H L,Ouyang S L,He Z J,Deng K,Zhao H P 2015J.Appl.Phys.117 164504

[21]Feng R 1999Ultrasonics Handbook(Danyang：Nanjing University Press)p128(in Chinese)[冯若1999超声手册(丹阳：南京大学出版社)第128页]

[22]http：//www.comsol.com/[2016-9-26]

[23]Lu M H,Liu X K,Feng L,Li J,Huang C P,Chen Y F,Zhu Y Y,Zhu S N,Ming N B 2007Phys.Rev.Lett.99 174301

[24]Zhu X F,Liang B,Kan W W,Peng Y G,Cheng J C 2016Phys.Rev.Appl.5 054015

[25]Cai F Y,Meng L,Zheng H R 2010J.Acoust.Soc.Am.128 1617

[26]Xu S J,Qiu C Y,Liu Z Y 2012Europhys.Lett.99 44003

[27]Hahn P,Leibacher I,Baasch T,Dual J 2015Lab Chip15 4302

PACS:43.25.Qp,43.20.+g,43.40.+s DOI:10.7498/aps.66.044301

Acoustic manipulation of particles by a resonant one-dimensional grating in air∗

Huang Xian-Yu1)2)Cai Fei-Yan2)†Li Wen-Cheng1)Zheng Hai-Rong2)He Zhao-Jian1)Deng Ke1)‡Zhao He-Ping1)

1)(College of Physics and Mechanical and Electrical Eengineering,Jishou University,Jishou 416000,China)
2)(Paul C.Lauterbur Research Center for Biomedical Imaging,Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences,Shenzhen 518055,China)

26 September 2016;revised manuscript

22 November 2016)

It is well known that acoustic wave carries momentum and energy.An object in a sound field,which absorbs or reflects sound energy,can be subjected to the acoustic radiation force(ARF),and thus can be manipulated in the contactless and noninvasive manners.This effect has potential applications in the fields of environment monitoring,microbiology,food quality control,etc.Obtaining a tunable trapping or pushing ARF should enable the design of an incident beam profile.However,the conventional acoustic manipulation system with plane wave,standing waves or Gaussian beams,which is usually generated directly by acoustic transducer,cannot be redesigned easily,nor can the corresponding ARF be modulated efficiently.Phononic crystals,which are artificial periodic structure materials,exhibit great advantages in modulating the propagation and distribution of acoustic wave compared with conventional materials,and thus have potential applications in tunable particle manipulation.Here,we present a theoretical study of the ARFs exerted on a cylindrical polystyrene foam particle near the surface of a one-dimensional(1D)grating in air.By using the finite element method(FEM)to investigate the transmission spectra and field distribution of the 1D grating and the FEM combined with momentum-flux tensor to obtain the ARF on the particle,we find that there are two resonance modes in the 1D grating,which origin from the coupling between the diffractive waves excited from the export of periodic apertures and the Fabry-Perot resonance mode inside the apertures.In addition,it can be seen from field distribution that in the first resonant mode,the resonance wavelength is approximate to the period of grating,and the enhanced spatial confinement of acoustic wave is located at the surface of the plate besides in the aperture.In the second resonant mode,the corresponding wavelength is more than twice the period of grating,and the enhanced spatial confinement of acoustic wave is mainly located in the aperture.Moreover,due to the gradient field distribution at the surface of slits and plate in these resonance modes,particles at the surface can be under the action of tunable negative ARFs.In thefirst resonance mode,the particle can be trapped on the surface of grating.While in the second resonance mode,the particle can be trapped in the aperture,and the amplitude of ARF of this mode is far smaller than that of the first mode.Thus,this system in the first resonance mode may have potential applications in air acoustic manipulation,aligning,and sorting micro-particles.

acoustic manipulation,acoustic radiation force,particle trapping,1D grating

:43.25.Qp,43.20.+g,43.40.+s

10.7498/aps.66.044301

∗国家自然科学基金(批准号：11274008,11325420,11404363,11564012,11304119,11304351)、深圳基础研究计划(批准号：JCYJ20150521094519482)、湖南省自然科学基金(批准号：2016JJ2100)和湖南省教育厅科研项目(批准号：16A170)资助的课题.

†通信作者.E-mail：fy.cai@siat.ac.cn

‡通信作者.E-mail：dengke@jsu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.11274008,11325420,11404363,11564012,11304119,11304351),the Shenzhen Basic Research Program,China(Grant No.JCYJ20150521094519482),the Natural Science Foundation of Hunan Province,China(Grant No.2016JJ2100),and the Natural Science Foundation of Education Department of Hunan Province,China(Grant No.16A170).

†Corresponding author.E-mail：fy.cai@siat.ac.cn

‡ Corresponding author.E-mail：dengke@jsu.edu.cn