基于新型磁控电抗器的静止无功补偿装置

赵国生，孙可钦，姚 珂

(1.郑州大学电气工程学院，河南郑州450002;2.河南南阳供电公司，河南南阳473000)

0 引言

随着电力机车、交流电弧炉、轧钢机以及其它大型半导体变流装置等冲击性负荷得到越来越广泛的应用，其带来的冲击无功分量和高次谐波分量直接导致了系统的电压闪变与波动，给电网造成了严重的影响，研制具有响应速度快、补偿性能好的静态无功补偿装置具有十分重要的意义.目前在10 kV及以上电压等级电网中应用广泛的静态无功补偿装置有基于TCR型SVC和基于磁控电抗器(MCR)型SVC，虽然响应速度较快，但产生的谐波较为严重.基于磁控电抗器(MCR)型SVC装置响应速度可以做到小于200 ms，其产生谐波含量较少，安全可靠，正越来越多地被广大用户所接受，目前广泛采用的是磁阀式磁控电抗器［1-6］.

1 新型磁控电抗器结构

新型磁控电抗器的电路拓扑结构如图1所示:

图1 新型磁控电抗器电路拓扑结构Fig.1 Structure of circuit topology of new magnetic controllable reactor

新型磁控电抗器的每相采用一个铁芯电抗器与一个磁阀式磁控电抗器(MCR)串联的结构，A、B、C三相中的绕组采用三角形连接.该新型磁控电抗器的铁芯和线圈的单相结构如图2所示.

新型磁控电抗器的每相有三个铁芯柱，其中铁芯柱Ⅰ、Ⅱ上含有几个截面积较小的段(分布式磁阀)，而第三个铁芯柱上不含磁阀，上、下磁轭采用与铁芯柱主截面相同的截面积.两个相邻铁芯柱Ⅰ、Ⅱ上的绕组交叉连接组成后再与第三个铁芯柱上的绕组串联构成三相中的一相，铁芯柱Ⅰ、Ⅱ上的绕组分上下两部分，每部分上都留有抽头，上、下两部分的抽头上连接着晶闸管，同一相两个铁芯柱上绕组引出抽头连接的晶闸管的极性相反，铁芯柱Ⅰ、Ⅱ上的绕组交叉连接后形成的绕组相当于图1中每相的交叉连接绕组，第三个铁芯柱上的绕组相当于图1中的铁芯电抗器绕组.图2中两个晶闸管与该Ⅰ、Ⅱ铁芯柱上的绕组产生电动势构成单相可控全波整流电路，改变晶闸管的触发角即可调整绕组中流过的直流控制电流，该直流控制电流在工作绕组中与交流工作电流叠加，但不流入第三个铁芯柱上的绕组与系统［1，4-5］.

图2 铁芯和线圈的单相结构Fig.2 Structure of the single phase iron and coils

在不加触发角情况下，虽然铁芯柱Ⅰ、Ⅱ上的绕组产生的感应电动势较小，但第三个铁芯柱上的绕组(相当于一个电抗器)的感应电动势起到了支撑作用，故总的线圈匝数可以选取的很小;当新型磁控电抗器工作在额定状态时，由于铁芯柱Ⅰ、Ⅱ上的绕组匝数较少，使得磁阀与磁轭部分的工作磁密得到有效的降低，因此大大减小了磁控电抗器的铜损及铁损.

2 磁阀大小的选择

在图2所示的新型磁控电抗器的铁芯结构中，磁阀的截面积选择及磁阀高度的确定取决于电抗器的容量大小.设Ⅰ、Ⅱ两柱每柱铁芯的磁阀高度为L，磁阀宽度为δ，磁阀截面积为Aδ，铁芯柱及磁轭截面积为A，当磁阀式磁控电抗器工作绕组中通过的电流为i时，由于磁阀部位的磁阻远大于铁芯的磁阻，根据安倍环路定律可得，N i=H L，因此有H=N i/L，设所选择铁芯材料的磁化曲线为B=f(H)，则磁阀磁密为

设磁阀面积为Aδ，铁芯面积为A，则铁芯磁通为

很多建筑工程项目中的施工管理存在疏漏，急需在第一时间内解决。例如，很多工程建设项目中的管理人员和施工人员不服从管理，违规施工问题屡见不鲜，从而对工程进度产生了极大影响。还有一些施工人员没有对安全防范意识提高重视程度，即使佩戴安全防护装置，也容易在工作中出现意外，再加上企业安全管理制度的内容不明确，无法实现施工现场安全问题的有效排除。当工程建设工作结束之后，部分施工企业的竣工检查工作流于形式，竣工质量无法把握，让建筑物在后续使用时暴露出质量问题。

式中:k为气隙影响系数，当阀柱比为1∶4时可近似取值为1.2，所以磁阀式磁控电抗器产生的感应电动势为

上式中第一项为磁性材料磁化曲线所决定的非线性项，第二项为空气所决定的线性项.由于新型磁控电抗器的感应电动势是其磁阀式磁控电抗器的感应电动势与串联铁芯电抗器的感应电动势之和，通常取第三个铁芯柱的截面积与Ⅰ、Ⅱ铁芯柱的截面积相等，设第三个铁芯柱上线圈匝数为NL，其磁阀大小与宽度可由下式求出:

3 电流谐波分析

设磁控电抗器支路流过的工作电流为i，直流控制回路电流为Id，控制绕组与工作绕组的匝数都为N，根据安培环路定律有

式中:f(B2)、f(B2)分别为左右铁芯的磁场强度;δ为每个铁芯柱磁阀长度，以上两式相加得

设直流控制电流在每个铁芯柱上产生的直流磁密为B0，交流工作绕组在每个铁芯柱上产生的交流磁密为 Bmcosωt，则有

定义铁芯的饱和度为

由于两铁芯绕组工作的对称性，

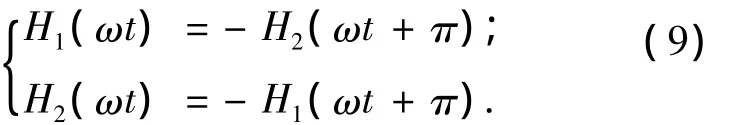
所以，电抗器电流中无直流分量和偶次谐波分量为奇函数，设其表达式为

对上式进行积分后，得

式中:I(2n+1)m为各奇次谐波电流幅值.

其基波电流幅值为

三相磁控电抗器采用三角形接线，其三次及其倍数次谐波无法通过.因此，其电流表达式为

4 仿真分析

新型磁控电抗器可以用图3所示的仿真模型来进行模拟仿真:

图3 新型磁控电抗器的仿真模型Fig.3 Simulation model of new magnetic controllable reactor

在图3所示仿真模型中，上部的两个串联变压器构成的整体为磁阀式磁控电抗器的仿真模型，它可以看成是两个变压器交流绕组同极性串联，其二次侧反极性串联后再加以可控直流电流.下边的串联电抗器为新型磁控电抗器中铁芯固定的电抗器模型，它相当于一个电感为L的固定电抗器.其可控直流电压Vd相当于磁阀式磁控电抗器改变不同触发角α后形成的可变电压源.图4(a)、(b)给出了增大触发角α后流过磁控电抗器中的电流变化情况的仿真结果.

图4 触发角α=175°，155°时，流过磁控电抗器的电流波形Fig.4 Current waveform of MCR at α =155°，175°

在触发角α=155°下，计算与仿真所得的流过磁控电抗器的谐波电流的结果比较如下表1(表中所给某次谐波结果的百分比是该次谐波电流有效值与基波电流有效值之比，以百分数表示):

表1 α=155°时计算与仿真所得的磁控电抗器谐波电流含量计算值和仿真值Tab.1 magnetic controlled controlled reactor harmonic current content after calculation and simulation whenα=155°

(1)从表1可以看出，在同一触发角下，磁控电抗器的电流仿真波形中的谐波电流含量的傅立叶谐波分析结果与表达式(14)中的结果相接近.

(2)通过图4的仿真结果比较可以看出，改变磁控电抗器的触发角，可以平滑地调节磁控电抗器绕组中流过的电流.

(3)从图2的新型磁控电抗器的单相结构图及公式(4)中可以分析出，由于第三柱铁芯柱中的磁通是铁芯柱Ⅰ、Ⅱ磁通之和，第三柱铁芯柱上每匝线圈产生的感应电动势是铁芯柱Ⅰ、Ⅱ上每匝线圈感应电动势的2倍，改进型磁控电抗器可以减少其线圈的总匝数，进而降低磁控电抗器自身损耗.

5 基于新型磁控电抗器的静止无功补偿［7-8］

基于新型磁控电抗器的静止无功补偿装置的电路结构如图5所示.

设滤波器FC提供固定的无功QC，可控电抗器提供感性无功QL，QF为负荷产生的无功.根据变电站的实际无功补偿要求，当要求实现无功功率恒定时，只要做到QF+QL+QC=定值即可.当要求实现功率因数恒定时，需要计算出其有功功率，然后按式(15)即可计算出磁控电抗器需要产生的无功功率QL，进而实现电网的功率因数恒定的要求.当控制系统对无功补偿的要求确定以后，满足补偿要求的任一时刻磁控电抗器支路需要产生的无功功率QL便可计算出来，设当前的功率因数为cosφ，功率因数的要求值为cosφN，则有

图5 基于新型磁控电抗器的静止无功补偿装置电路结构Fig.5 Circuit structure of static reactive based on new magnetic controllable reactor

磁控电抗器支路流过的无功电流为

设每相串联的固定铁芯电抗器的电抗值为L，，固定电抗器的电压降为ωLIL，则磁控电抗器的压降为

取额定容量时(α=180°)磁控电抗器的电压降与电网电压之比为η，空载时(α=0°)磁控电抗器的电压降与电网电压之比为λ，则磁控电抗器的额定电流与空载电流分别为

当晶闸管的触发角为α时磁控电抗器流过的电流IL可以表示为

式中:β为对应晶闸管触发角α时的磁饱和度，它与晶闸管的触发角α关系为

由以上关系式即可求出任意时刻满足补偿要求的晶闸管的触发角α.

控制软件的控制流程如图6所示:

图6 控制流程Fig.6 Control flow

6 结论

提出了一种新型磁控电抗器，对该磁控电抗器的电路结构、铁芯结构及该基于新型磁控电抗器的静态无功补偿装置进行了介绍，并从理论上对磁控电抗器的工作原理、触发角计算、铁芯磁阀的选取及工作电流中的谐波进行了数学分析及模拟仿真分析，最后对控制电路及控制流程进行了介绍.所提的新型磁控电抗器通过减小绕组的匝数可以减少磁控电抗器的自身功率损耗.

［1］ 陈柏超.新型可控饱和电抗器理论及应用［M］.武汉:武汉水利电力出版社，1999.

［2］ 赵晶，余梦泽.新型高压磁控电抗器的电压/无功控制效果分析［J］.供用电，2008，25(5):35-37.

［3］ 周立霞，尹忠东.可控电抗器及其谐波抑制的研究［J］.现代电力，2006，23(2):10-14.

［4］ 陈柏超，田翠华.谐波双级饱和磁控电抗器研究［M］.电工技术学报，2006，21(1):19-23.

［5］ 尹忠东，刘虹，陈柏超，等.磁阀式可控电抗器的研究［J］.变压器，1998，35(7):1-5.

［6］ 清华大学工业自动化系.饱和电抗器原理与设计［M］.北京:清华大学，1977.

［7］ 郑研，王克文.静止无功补偿装置的理想补偿电流［J］.郑州工业大学学报:自然科学版，2001，22(4):107-109.

［8］ 余梦泽，陈柏超，田翠华，等.采用磁控电抗器的静止型高压动态无功补偿装置［J］.高电压技术，2009，35(7):1770-1774.