智能电表条形码图像分割与增强算法研究
谢 钢,林茂松,代彦辉
(西南科技大学信息工程学院,四川绵阳621010)
0 引言
在国家大力发展智能电网(Smart Grid)的背景下,智能电表作为智能电网建设的重要基础元件,加快智能电表产业链整合,促进其产业化,对于电网实现信息化、自动化和互动化具有支撑作用.随着国网公司计量管理方式的转变和科学技术的进步,要求计量中心能够实现智能电表检定的无人化、自动化,然而目前智能电表自动检定技术在电能计量中心尚未有应用.
要实现基于机器视觉的智能电表全自动检测,需要对智能电表身份识别,在此基础上对智能电表上的液晶屏、铭牌区域图像进行精确分割,实现液晶屏和铭牌区域的自动外观检测,这是当前智能电表自动化检定的迫切需求,也是推进电能计量应用技术发展的新课题.实现智能电表自动化检定的关键是自动识别智能电表的一维条码信息.当前一维条形码的识别算法已经很成熟[1],准确识别条形码信息的关键是条形码的精确分割和条码图像纹理信息的增强,然而当前关于智能电表图像研究还处于一个空白阶段.本文源于国家电网公司研发课题智能电表检定机器人研究,针对目前国家电网公司流通的智能电表提出了一种通用可靠的条形码定位与识别方法.
1 图像去噪
在智能电表检定环境下所采集的图像都是受到噪声干扰的,由于采集的图像信号可近似地看成平稳随机过程,当信号与噪声同时输入时,采用维纳滤波器可以在输出端将信号尽可能精确地重现,且噪声受到最大抑制.维纳滤波器的算法思想是使之间的均方误差达到最小的准则函数来实现原始图像信号的去噪[2],即

式中:E{·}代表期望值的计算.因此维纳滤波器是一种最小均方误差滤波器.
设原始图像、退化图像和图像噪声为f(x,y),g(x,y),n(x,y),维纳滤波图像退化模型如图1所示.

图1 图像退化过程模型Fig.1 The model of image degradation processing
其一般表达式为:

式中:h(x,y)是退化函数的空间描述,也称为成像系统的冲击响应或点扩展函数(PSF);“*”表示卷积.由于空间上的卷积可等同于频域上的乘积,等式(2)具有如下等价形式:

对原始图像(假设图像大小为H*L)进行维纳滤波的算法.首先是估计出每个像素点M*N邻域内的平均值和方差值,有如下两个表达式:


式中:v2为噪声方差,将式(6)代入等式(3)中,得其在频域中的表达式如下:


2 锐化图像
为了能够准确分割智能电表上的条形码区域,需要突出条码区域.根据条形码是由黑白相间的矩形长条组成,采用基于一阶微分的Sobel算子锐化图像[3],突出条形码区域.Sobel算子的基本模板如图2所示.

图2 Sobel算子模板Fig.2 Sobel operator template
将图像分别经过两个3×3算子的窗口滤波,所得结果按式(8)给出,就可得到增强后图像的灰度值.

式中:
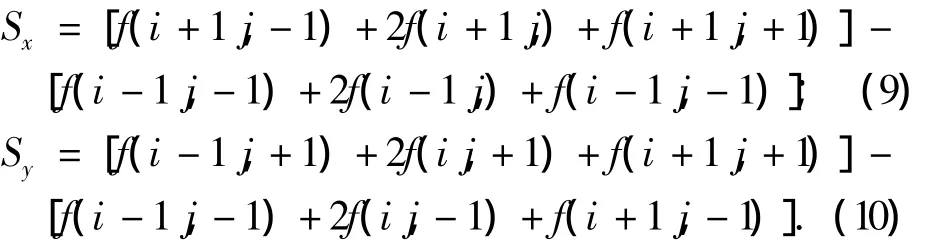
式(9)和式(10)分别对应如图2所示的两个滤波模板.为了简化计算,也可以用g=|Sx|+|Sy|来代替式(8)的计算,从而得到锐化后的图像.
3 智能电表条形码图像增强
由于实际光照环境的影响,采集到的条形码区域图像比较模糊,对条码的细节信息提取增加了难度.常用的图像增强算法有:冥次变换局部增强方法,主要依赖于变换函数和窗口大小的选取,且计算量大[4];直方图均衡化方法,主要是通过变换函数将原始图像的直方图调整为平坦的直方图,不能很好地保留图像的纹理信息[5];基于小波变换的增强方法,主要依赖于小波函数的选取,小波变换通常能够较好地保留图像的纹理特征[6].常用的小波变换方法有Mallat小波变换和提升小波变换.提升小波具有结构简单、运算量低、原位运算、存储空间较小、逆变换可以直接反转实现,以及整数到整数变换可逆的特点,但是提升小波变换后低频部分的细节信息被削弱了[7],在提升小波的基础上,对其变换过程中细节信息进行重新构造.
3.1 改进的提升小波变换
提升算法给出了双正交小波简单而有效的构造方法,它使用基本的多项式插补来获取信号的高频分量,然后通过“保持原信号的均值和高阶矩不变”的限制条件来获取信号的低频分量.提升算法的基本思想是,将现有的小波滤波器分解成基本的构造模块,分步完成小波变换[8-9].
考虑有2n个样本值的信号Sn,通过变换将其分解成一个表示信号全局信息的信号Sn-1和一个表示细节信息的信号dn-1,提升算法方案将通过分裂、预测和更新三步来完成,如图3所示.

图3 提升小波变换示意图Fig.3 The diagram of lifting wavelet transform
3.1.1 分裂
将输入信号Sn分为较小的子集Sn-1和dn-1,根据输入信号Sn奇偶性将输入信号分解成偶信号Sn-1、奇信号dn-1,这种分裂所产生的小波称为惰性小波,分解过程表示为F(Sn)=(Sn-1,dn-1),分解过程如图4所示.这种分解方法充分利用了信号Sn的局部相关性,为提升方案后面的预测和更新步骤提供了数据基础.

图4 信号分裂Fig.4 The signal splitting
3.1.2 预测
在基于原始数据相关性的基础上,用偶数序列Sn-1的预测值P(Sn-1)去内插奇数序列dn-1,即将滤波器P对偶数序列作用以后的值作为奇信号的预测值,奇信号的实际值与预测值相减得到残差信号,该差值的大小体现了二者之间的逼近程度,残差越小表明预测越精确,拟合程度越好。实际中利用P(Sn-1)和dn-1的差来代替原来的dn-1,若P(Sn-1)选择合理的话,新的差值数据集dn-1包含的信息量大大少于原始子集中包含的信息量.
采用Harr小波进行预测,偶数序列的样本值用来预测奇数序列的样本值,细节信息dn-1就是奇数序列样本值和预测值之差:

在提升过程中,预测有两个作用:一是可以分离出信号的高频分量;二是可以紧凑表示数据.本文预测算法P(·)为信号相邻两个样本的平均.实验结果表明,该预测算子能够得到比较好的逼近效果,对于边缘扩展采用周期延拓处理,这种处理方式能够很好地保留边缘的细节信息.
3.1.3 更新
为了使原信号某些全局特征信息在其子集Sn-1中继续保持,必须进行更新处理,更新的步骤紧跟在预测之后.全局信息Sn-1需要保持原始信号Sn的平均信息:

式中:U(·)为更新函数;在Harr小波中,Sn-1为奇偶样本对的平均值,即

然后从预测步骤中恢复原始信号的样本值:

将(14)代入(13)中,得到


由上可知,通过原位运算就不需要前级提升步骤的输出之外的数据,这样在每个点都可以用新的数据流替换旧的数据流.
3.2 小波多分辨率
利用改进后的提升小波变换对图像进行多分辨率分析,对一幅图像进行多分辨率分解以后,会产生四个二维正交小波分解系数,它们每一个都可以看作一幅图像,笔者采用三层提升小波算法进行多分辨分析如图5所示.

图5 三层提升小波变换示意图Fig.5 Three-tier lifting wavelet transform schematic
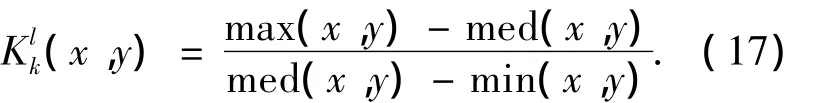
式中:max(x,y),med(x,y),min(x,y)分别表示小波系数中的最大值、均值和最小值.
4 实验结果与分析
笔者在WindowsXP下,以Visual studio 2008为开发平台,利用C++编程实现智能电表条形码的自动定位与身份识别.图6(a)是智能电表的灰度原始图像,图像噪声信息明显.图6(b)经过维纳滤波器处理后的图像,有效的消除了噪声,图像平滑,整体视觉效果好.图6(c)是利用Sobel算子对去噪后的图像进行锐化,从图中可以看出,条形码区域明显突出,之后通过图像二值化和行列扫描便可精确分割出条形码区域,如图7(a)所示.可以发现条形码区域的图像信息对比度较低,纹理信息模糊.图7(b)是基于局部增强算法对条形码区域图像增强的结果,图像整体得到了明显增强,但是图像信息不太平滑,出现了一定的振铃现象.图7(c)是基于直方图统计对条形码区域图像增强的结果,图像的细节和噪声信息都得到了增强,整体视觉效果不太好.图7(d)是基于传统提升小波多分辨率图像增强的结果,图像的纹理信息得到了很明显的增强,但是图像的细节信息被削弱了.图7(e)是基于改进的提升小波多分辨率增强算法对条形码区域图像增强的结果,该处理方法在增强图像细节的同时,压缩了噪声,并对图像进行整体增强,图像较平滑,图像的整体视觉效果好.

图6 图像预处理Fig.6 The image Pre-prololy

图7 图像增强后的结果Fig.7 The image enhancement results
5 结束语
为了填补基于机器视觉的智能电表自动检测技术在电能计量中心的研究空白,对智能电表条形码区域图像分割与增强技术研究.笔者利用维纳滤波去噪效果明显,通过Sobel算子突出条形码区域,之后通过图像扫描达到精确分割条形码区域的目的,该方法在当前流通的智能电表中具有通用性并且条形码区域定位准确.然而往往实际采集到的条形码区域都比较模糊,为了能够准确无误地解码出条形码,需要对条形码区域进行增强,笔者提出了一种改进的提升小波多分辨率方法,从整体上增强图像的细节纹理特征,使增强后的图像较平滑,图像的整体视觉效果好,为能够正确识别条码信息提供了可靠保证.
[1] 谢俊喜.基于数字图像处理的条形码识别方法与应用研究[D].长沙:中南大学信息工程学院,2008.
[2] 张德丰,张葡青.维纳滤波图像恢复的理论分析与实现[J].中山大学学报,2006,45(6):45-47.
[3] 朱秀昌,刘峰,胡栋.数字图像处理与图像通信[M].北京:北京邮电大学出版社,2008.
[4] 冈萨雷斯.数字图像处理[M].第二版.北京:电子工业出版社,2007.
[5] BRADSKI G,KAEBLER A.学习 OpenCV(中文版)[M].于仕琪,刘瑞祯,译.北京:清华大学出版社,2009.
[6] 宋娜.基于小波分析的车牌图像增强与字符识别研究[D].重庆:重庆大学信息工程学院,2010.
[7] 倪林.小波变换与图像处理[M].合肥:中国科学技术大学出版社,2010.
[8] 韩丽娜,耿国华.基于小波变换的真彩图像降噪和增强[J].计算机工程,2010,36(12):224-228.
[9] CHANG S G,YU B,MARTIN V.Adaptive wavelet thresholding for image denoising and compression[J].IEEE Transactions on Image Processing,2000,9(9):1532-1546.

