一种单位分解三角形单元及其在动力响应分析中的应用
贾 程,陈卉卉
(盐城工学院土木工程学院,江苏盐城224051)
0 引言
目前,有限单元法已经被广泛地应用于解决各种工程问题,但该方法仍然存在一些缺陷.传统的有限单元法通常采用协调模型,使得刚度矩阵“过刚”,能导致计算所得位移和应力的精度下降,尤其对线性三角形单元而言更为明显;能使得等参单元对网格畸变敏感.学者们提出了许多提高有限元精度的方法,如非协调模式法[1-2]、四边形面积坐标法[3]、无网格法[4-5]等.近些年来,单位分解法[5-6]引起了研究者的注意.单位分解有限元法较普通有限元的优点是不需增加额外的节点,就能构造高阶的场函数,这为创建高效的单元格式提供了一种方法.另外,它能够自由地选择局部近似函数,这使其便于分析复杂问题.
笔者采用线性三角形“单元”形函数作单位分解函数,利用最小二乘法建立局部近似场函数进而构造有限元无网格耦合三角形单元.其形函数具有Kronecker delta性质.通过分析二维固体的自由振动和强迫振动响应,表明该单元没有虚假的零能模式,计算结果的精度优于线性三角形单元和线性四边形等参元.
1 有限元无网格耦合三角形单元公式
1.1 有限元无网格耦合三角形单元的形函数
对于二维线弹性问题,采用三角形网格离散问题域,如图1所示.单元内任一点的位移可表示成:

其中:N'= [N1,N2,N3]是传统的线性三角形单元的形函数矩阵[7];ue={u1(x,y)u2(x,y)u3(x,y)}T是局部节点位移函数.在该节点处等于其位移值,即 ui(xi,yi)=ui,i=1,2,3.局部节点位移函数ui(x,y)利用Rajendran等[6]使用的最小二乘点插值无网格法(LSPIM),由i点的支持域内的节点值拟合得到:

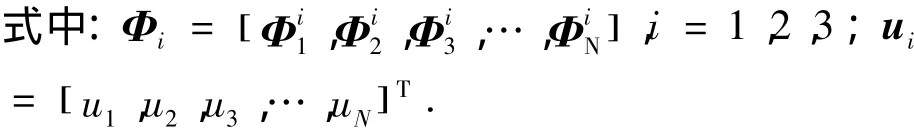
其中,Φi是LSPIM法的关于节点i的形函数矩阵,ui是节点i支持域内节点的位移参数向量,N为节点i支持域内的所有节点数.一个单元所有节点支持域的合集构成了一个单元的支持域Ω.
节点支持域和单元支持域的定义如图1所示:
将式(2)带入式(1),得
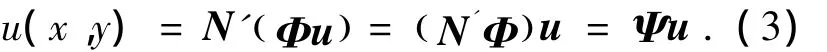
从方程(3)中,可以得到该单元的形函数矩阵,设单元支持域Ω内的节点数为M:


图1 支持域的定义Fig.1 Definition of the support.
1.2 局部节点位移函数的形函数Φi
局部节点位移可以写成下列形式:

为方便起见,该单元的第一个节点记为节点i.
由于传统的最小二乘近似a=(PTP)-1PTui使得节点i的位移近似值不等于该点的位移值,即ui≠p(xi,yi)a,导致位移条件施加比较困难.故为了使节点i的位移近似值等于该点的位移值,利用方程(5)中的第一个方程解出a1,再从方程(5)其余的方程中消去a1,可得
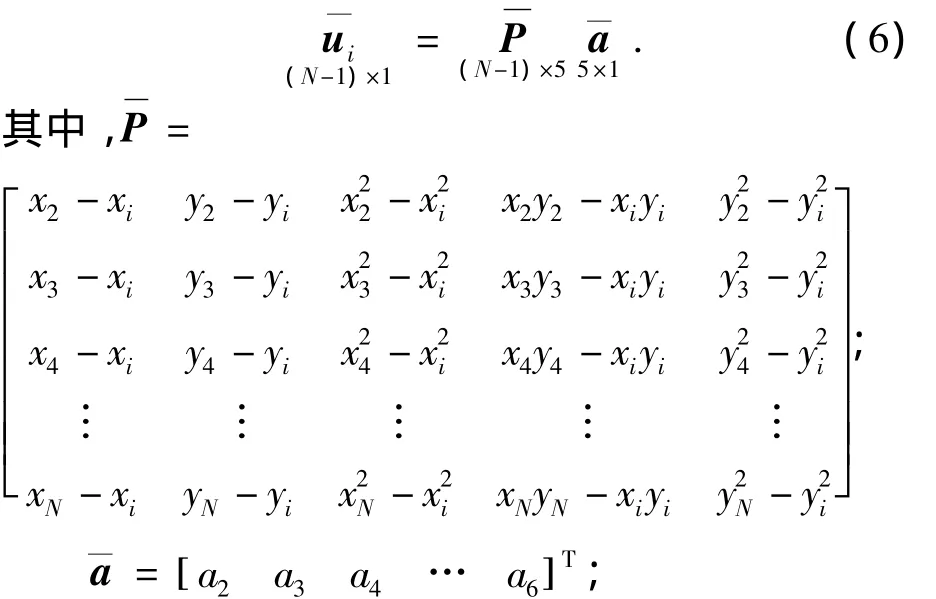

则由最小二乘法得

节点i邻域内位移又可以表示为

则
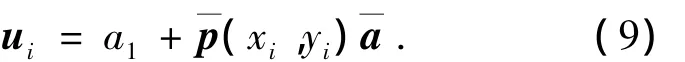
并将式(7)、(9)带入式(8)可得ui(x,y)表达式
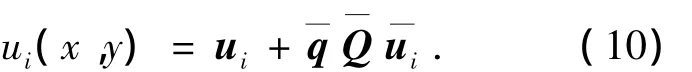

ui(x,y)表达式(10)可简写成:

此处,Φi为局部节点位移函数的形函数,可写成:
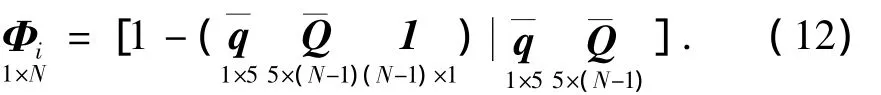
其中1为所有元素均为1的(N-1)行列向量,利用式(4)进而可以求出单元的形函数矩阵Ψ.
从式(10)可以看出,对于(xi,yi)点存在ui(xi,yi)=ui,再根据式(4)可得 Ψ = [1,0,0|0,…,0].同理对于 i=2,3 点,存在.故该有限元无网格耦合三角形单元的形函数具有Kronecker delta性质,能够像普通的有限元一样直接施加位移边界条件.
1.3 自由振动和强迫振动分析
由哈密顿原理,可得系统的运动方程为
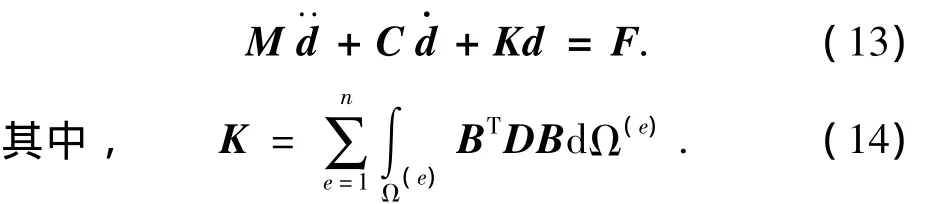
为有限元无网格耦合三角形单元的刚度矩阵,位移应变矩阵B的维数是3×2M,M为单元支持域Ω内的节点数.
M为质量矩阵:
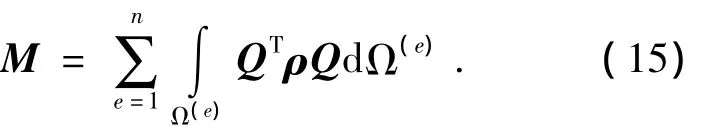
其中,Q是(4)式中元素组成的2×2M矩阵.
C为阻尼矩阵,为简便起见,取瑞利阻尼:

其中α,β是瑞利阻尼系数.
荷载列阵F:

文中运动方程(13)的求解采用Newmark方法[7-8],求解参数取 α =0.25,δ=0.5.
若阻尼和荷载项为零,则得自由振动方程:
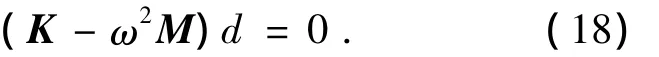
2 数值算例
2.1 锥形梁的自由振动
如图2(a)所示锥形悬臂梁,梁厚t=0.05 m,弹性模量E=200 GPa,泊松比 μ=0.3,ρ=8 000 kg/m3,为了与四边形等参元比较,采用6×4形式划分网格,如图2(b)所示,四边形采用畸变的网格.前六阶频率计算结果列于表1.

图2 锥形梁的几何模型和网络Fig.2 The geometry and mesh of the taper beam
从表1可以看出,有限元无网格耦合三角形单元没有出现虚假的零能模式,并且其结果的误差远小于线性三角形单元(FEM-T3)和四边形等参元(FEM-Q4).
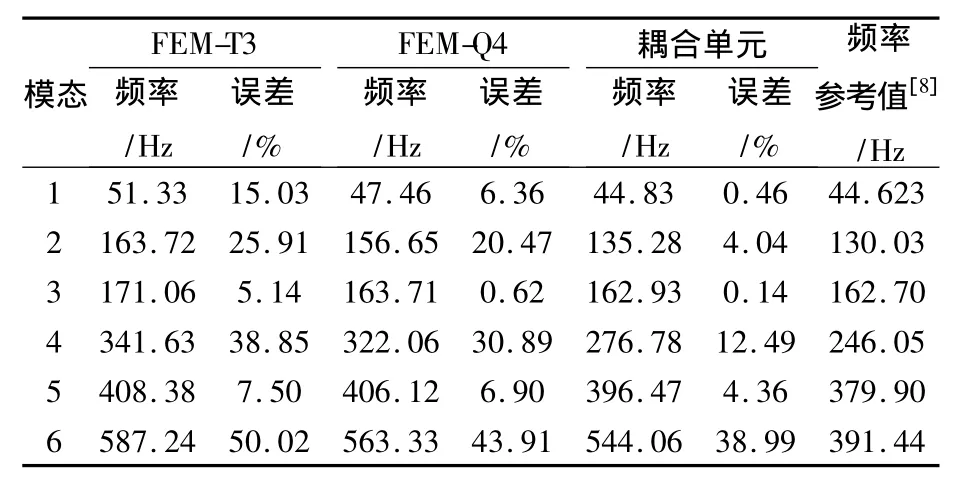
表1 锥形梁的固有频率Tab.1 The natural frequencies for the taper beam
2.2 悬臂梁的强迫振动
如图3(a)所示矩形悬臂梁,弹性模量E=1Pa,μ =0.3,ρ=1.0 kg/m3,瑞利阻尼系数 α =0.005,β=0.272.采用10×4划分网格,如图3(b)所示.考虑两种荷载工况.
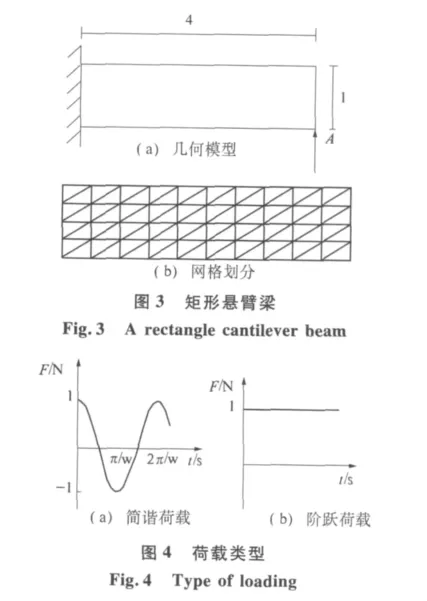
(1)如图4(a)所示,在A点受一集中简谐荷载F(t)=cos(ωt),ω =0.3,计算时间取t=100 s,时间步长取Δt=1 s.图5绘出了考虑阻尼时,线性三角形单元(FEM-T3)、四边形等参元(FEMQ4)、八节点等参元(FEM-Q8)、本文耦合单元以及理论解[9]的A点竖向位移的动力响应.从图上可以看出,本文耦合单元和八节点等参元的振幅都非常接近理论解,精度比四边形等参元高,远优于线性三角形单元.图6为无阻尼时,4种单元和理论解[9]的动力响应,同样可以看出,本文耦合单元的结果更接近理论解和八节点等参元,比四边形等参元和线性三角形单元精确.
上例自由振动和本例的结果说明笔者所提的耦合单元能够应用到动力响应分析中,并且具有较高的计算精度.
(2)如图4(b)所示,t=0 s在A点受一突加集中荷载F=1 N,持续时间t=2 000 s,时间步长取Δt=1 s.利用笔者所提的耦合单元,计算A点竖向位移的动力响应,其结果与理论解[9]一并绘于图7.
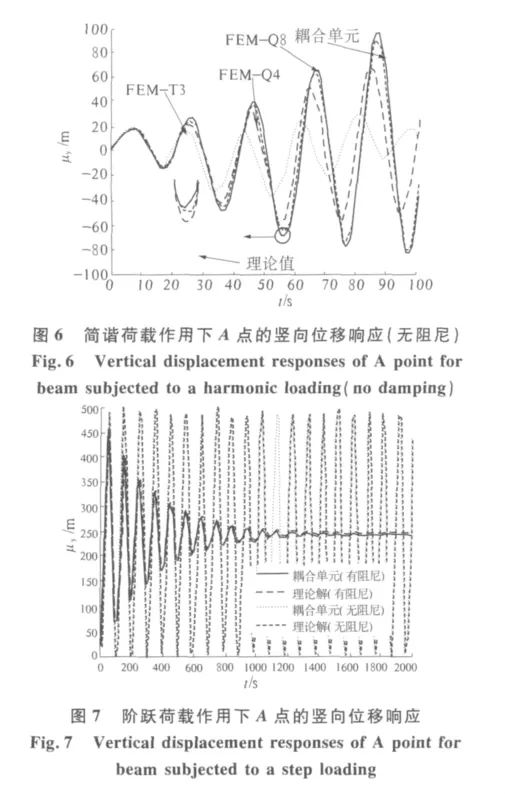
从图7同样可以看出,该耦合单元精度较高.在没有阻尼时,A点在做振幅是接近常数的受迫振动.考虑阻尼时,由于阻尼的作用,位移的振动响应随着时间的延长而迅速衰减,直至消失.
3 结论
将有限元无网格耦合三角形单元应用于分析二维固体的自由振动和强迫振动响应.通过典型的数值算例计算表明,该单元不存在虚假的零能模式,计算响应的振幅接近八节点等参元,其精度优于线性三角形单元和线性四边形等参元.该单元还可以应用到板、壳等结构的动力分析中.
[1] WILSON EL,TAYLORR L,DOHERTY WP,et al.Incompatible Displacement Modes in Numerical and Computer Models in Structural Mechanics[M].New York:Academic Press,1973:43-57.
[2] 秦力一,许德刚,周爱民.基于切应力条件的广义协调等参元[J].郑州大学学报:工学版,2005,26(2):92-94.
[3] 龙驭球,李聚轩,龙志飞,等.四边形单元面积坐标理论[J].工程力学,1997,14(3):1-11.
[4] BELYTSCHKO,LU Y Y,GU L.Element free Galerkin methods[J].International Journal for Numerical Methods in Engineering,1994,37(2):229–256.
[5] BABUSˇI,MELENK JM.The partition of unity method[J].International Journal for Numerical Methods in Engineering,1997,40(4):727–758.
[6] RAJENDRAN S,ZHANG B R.A “FE-meshfree”QUAD4 element based on partition of unity[J].Computer Methods in Applied Mechanics and Engineering,2007,197(1-4):128 –147.
[7] 陈国荣.有限单元法原理及应用[M].北京:科学出版社,2009:310-319.
[8] ABBASSIAN F,DAWSWELL D J,KNOWLES N C.Free Vibration Benchmarks[M].Glasgow:National Agency for Finite Element Methods & Standards,1987:72-77.
[9] 克拉夫,彭津.结构动力学[M].北京:高等教育出版社,2006:308-314.

