带有p-Laplacian算子的分数阶微分方程多点边值问题正解的存在性

张 艳，马德香

（华北电力大学数理学院 北京 102206）

带有p-Laplacian算子的分数阶微分方程多点边值问题正解的存在性

张 艳，马德香

（华北电力大学数理学院 北京 102206）

在以下带有p-Laplacian算子的分数阶微分方程多点边值问题中：

其中Dα，Dβ是Riemann-Liouville分数阶导数，f∶［0，+∞）→［0，+∞）是连续函数，文章的新奇之处在于运用Guo-Krasnoselskii不动点定理来研究了一类含参量的带有p-Laplacian多点边值问题正解的存在性及不存在性.

分数阶微分方程；p-Laplacian算子；多点边值问题；不动点定理

0引言

分数阶微分方程边值问题近年来得到了很多学者的关注，具体见参考文献[1-7]，然而直到近几年带有p-Laplacian算子的分数阶微分方程边值问题的研究才开始兴起，这是因为由其建立的模型在多孔介质中的湍流现象，在流变学、材料科学、粘塑性力学等领域有着广泛应用，研究带有p-Laplacian算子的分数阶微分方程边值问题具有较大的研究前景.近年来有一些作者开始研究带有p-Laplacian算子的分数阶微分方程边值问题，例如在文献[8]中，作者陈泰永运用重合度理论研究了以下带有p-Laplacian算子的分数阶微分方程两点边值问题：

在文献[9]中，作者韩振来通过运用Guo-Krasnoselskii不动点定理研究了以下带有p-Laplacian算子的分数阶微分方程两点边值问题：

受以上文献启发，本文将运用Guo-Krasnoselskii不动点定理来研究以下边值问题

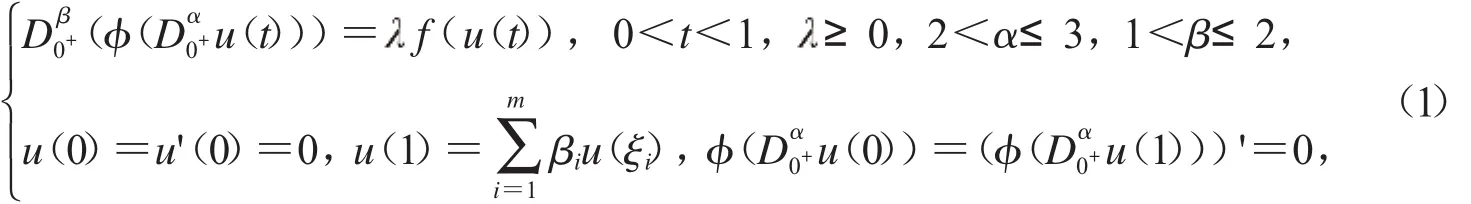
在本文中，假设以下是成立的：

（H2）f∶［0，+∞）→［0，+∞）是连续的；

（H3）φ∶R→R为非减奇函数，且存在非减同胚映射Ψ1，Ψ2，满足

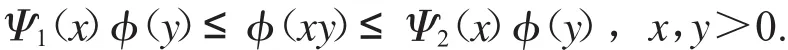
1 预备知识和引理

1.1 预备知识

1.1.1 α＞0，定义函数y∶（0，∞）→R的α阶Riemann-Liouville分数阶积分为

其中Γ（·）是欧拉积分，等式右端在（0，∞）上逐点定义.

1.1.2 α＞0，定义函数y∶（0，∞）→R的α阶Riemann-Liouville分数阶导数为

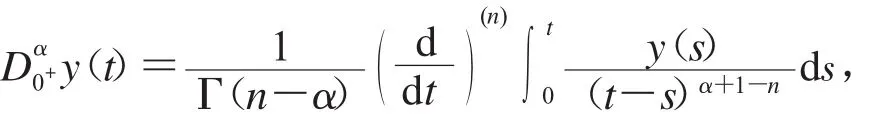
其中n＝[α]+1，等式右端在（0，∞）上逐点定义.

1.2 引理

1.2.1 假设α＞0，若u∈C（0，1）∩L（0，1）有α阶Riemann-Liouville导数，则

其中N为大于或等于α的最小整数.

1.2.2[10]设x∈C+[0，1]:＝{x x∈C[0，1]，x（t）≥0，t∈[0，1]}.下列边值问题：

其中

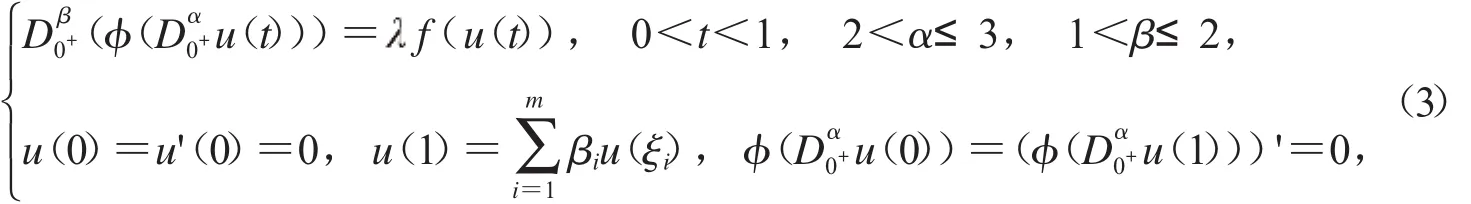
有唯一解

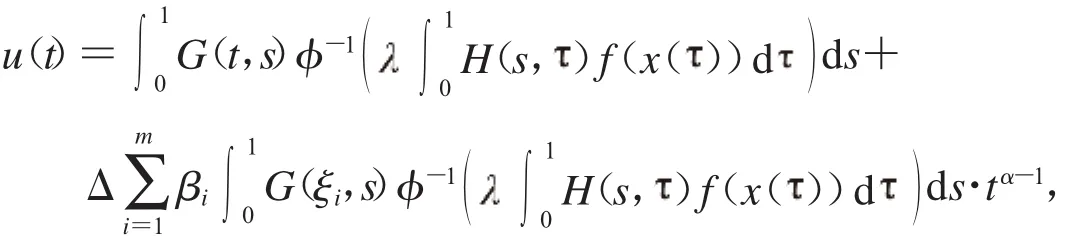
其中G（t，s）见式（2），而证明：

根据引理1.2.1和1＜β≤2，得

由式（3），有

即

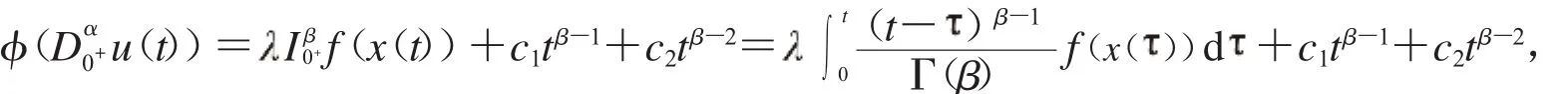
因此：

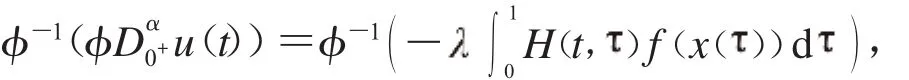
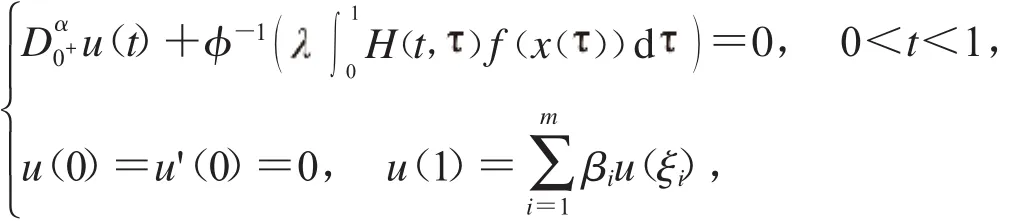
那么根据引理1.2.2，可知式（3）有唯一解

证明完成.

1.2.4[11]G（t，s）有下列性质：

（1）对于任意的（t，s）∈[0，1]×[0，1]，G（t，s）≥0.（2）给定s∈[0，1]，则对于任意的t∈[0，1]，

（3）给定s∈[0，1]，则对于任意的t∈[0，1]，有G（t，s）≥ρ（t）G（t0，s），其中

1.2.5[12]H（s，）有以下性质：

1.2.7[14]（Guo-Krasnoselskii不动点定理） E为Banach空间，P⊂E是一个锥，设Ω1，Ω2是E中的两个有界开子集，且θ∈Ω1⊂Ω1⊂Ω2，有T∶P∩（Ω2Ω1）→P为全连续算子，且满足

（1）Tu≤u，u∈P∩∂Ω1，Tu≥u，u∈P∩∂Ω2，或者

（2）Tu≥u，u∈P∩∂Ω1，Tu≤u，u∈P∩∂Ω2，

则算子T在P∩（Ω2Ω1）中存在不动点.

定义算子T∶P→P如下：

1.2.8 T∶P→P是全连续算子.

证明：由引理1.2.4，得

下面证明T的紧性，设Ω⊂P是有界的，则存在正常数M＞0，对于所有的u∈Ω，有u≤M.令k＝max+1.当u∈Ω，t∈[0，1]时，有

因此，T（Ω）是一致有界的.

另一方面，因为G（t，s）在[0，1]×[0，1]上是连续的，在[0，1]×[0，1]是一致连续的，因此对于任意的ε＞0，存在δ＞0，当t1，t2∈[0，1]，当t1-t2＜δ，有

对于所有的u∈Ω，

因此T（Ω）是等度连续的.再由Arzela-Ascoli定理，可知T是紧的，从而得到T∶P→P是全连续算子.证明完成.

2 正解的存在性与不存在性

为方便起见，引入以下符号，

2.1 正解存在性定理的证明

分数阶微分方程（1）至少有一个正解.（当f∞＝+∞，F0＝0时，记f-∞1＝0，F0-1＝+∞.）

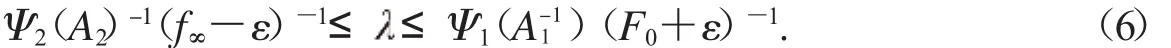
以下证明分为两部分.

第一步：由F0的定义可知，r1＞0，

对于u∈P且u ＝r1，

取Ω1＝{u∈E＜r1}，有

第二步：由f∞的定义可知，r3＞0

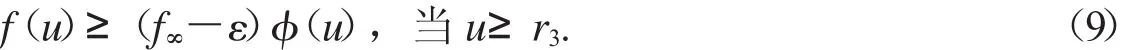
取r2＞ r3，如果u∈P且u ＝r2＝max{2r1，r3}，由式（6）和（9）可得

故Ω2＝{u∈E＜r3}取，得

根据式（8）、（10）以及定理1.2.7可得，T中有一个不动点u∈P∩（Ω2Ω1）且满足r1≤u ≤r2，显然u就是分数阶微分方程边值问题（1）的正解.证明完成.

f0Ψ（1A-11）＞F∞Ψ（2A-21）成立.那么对于则分数阶微分方程（1）至少有一个正解（.当f0＝+∞，F∞＝0，有f-01＝0，F-∞1＝+∞.）证明：当满足式（11），可知 ε＞0，满足

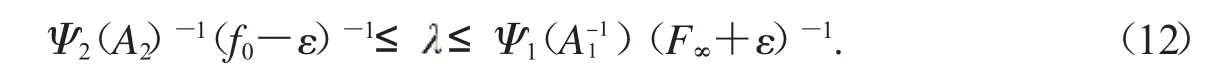
以下证明分为两部分.

第一步：由f0的定义可知，r1＞0，

对于u∈P且u ＝r1，类似于定理2.1.1第二部分的证明方法，可取Ω1＝{u∈Eu ＜r1}，有

第二步：选取R1＞0

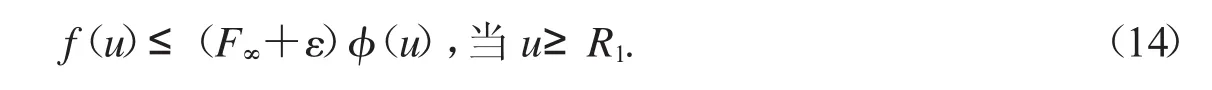
接下来，考虑两种情况：

情况一：假设f是有界的.N＞0，有

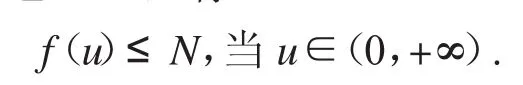
取r3＝max{2r1，φ-（1N）A1}，对u∈P且u＝r3，有

情况二：假设f是无界的.则存在r4＞max{2r1，R1}使得

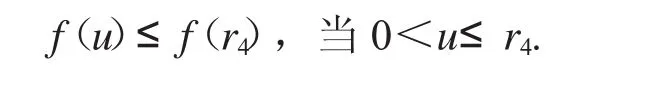
对于u∈P且u ＝r4，

取Ω4＝{u∈Eu＜r4}有T u≤u ，当u∈P∩∂Ω4.

再由情况一和情况二可知，当Ω2＝{u∈Eu ＜r2＝max{r3，r4}}，有

根据定理1.2.7和式（13）、（15）可知，T中有一个不动点u∈P∩（Ω2Ω）1且满足r1≤u≤r2，显然u就是分数阶微分方程边值问题（1）的正解.证明完成.

2.1.3 假设r2＞r1＞0，有

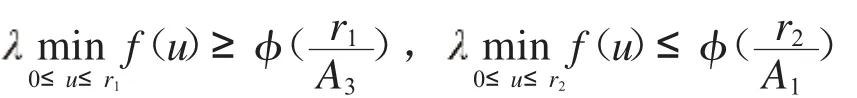
则分数阶微分方程（1）边值问题有一个正解u∈P且r1≤u ≤r2.

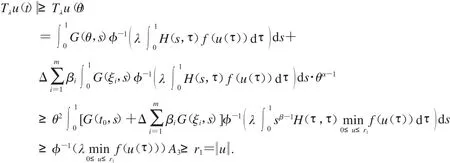
取Ω2＝{u∈Eu ＜r2}.当u∈P∩∂Ω2，有

因此，由定理1.2.7知，分数阶微分方程（1）的边值问题有一个正解u∈P且r1≤u ≤r2.证明完成.

2.1.4 假设f0＝+∞，f∞＝+∞.那么对于∈（0，1），则分数阶微分方程（1）边值问题至少有两个正解，其中

证明：令x（r）＝由f的连续性可知，x（r）∶（0，+∞）→（0，+∞）是连续的.

一方面，根据f0＝+∞，f∞＝+∞，可得limx（r）＝limx（r）＝0.故存在r0∈（0，+∞），使得x（r0）＝supx（r）＝1.对于∈（0，1），存在常数a1，a（20＜a1＜r0＜a2＜+∞）有

则，

另一方面，根据f0＝+∞，f∞＝+∞，存在常数b1，b（20＜b1＜a1＜r0＜a2＜b2＜+∞）有

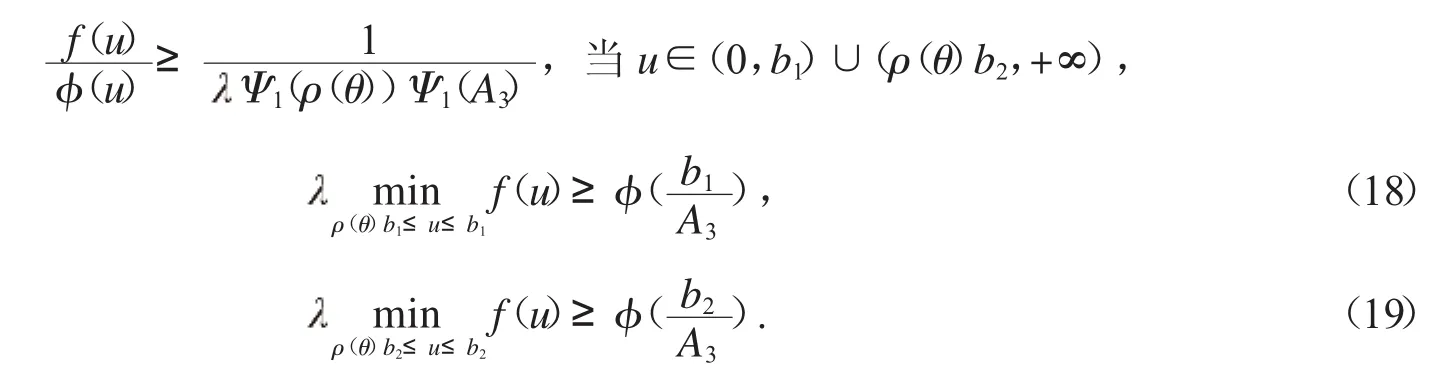
再由式（16）-（19）并根据定理2.1.3和定理1.2.7可得，当∈（0，1）时，分数阶微分方程边值问题（1）至少有两个正解.

2.2 正解不存在性定理的证明

2.2.1 假设F0＜+∞，F∞＜+∞.那么存在0＞0，0＜＜0，分数阶微分方程边值问题（1）无正解.

证明：根据F0＜+∞和F∞＜+∞可知，存在正常数M1，M2，r1，r2，使得当r1＜r2时，满足

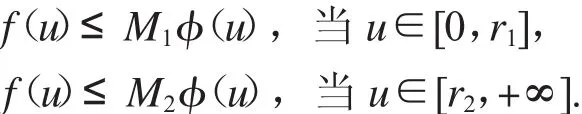
假设v（t）是分数阶微分方程边值问题（1）的正解.当0＜＜0:＝M-01Ψ（1A-11），对于t∈[0，1]，有T v（t）＝v（t），因此有

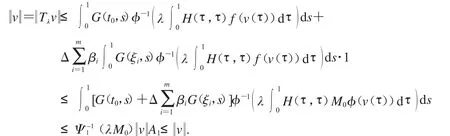
与T v（t）＝v（t）相矛盾，因此分数阶微分方程边值问题（1）无正解.证明完成.

2.2.2 假设f0＞0，f∞＞0.对于0＞0，＞0，分数阶微分方程边值问题（1）无正解.证明：根据f0＞0和f∞＞0，存在正常数m1，m2，r3，r4，使得当r3＜r4，

与T v（t）＝v（t）相矛盾，分数阶微分方程边值问题（1）无正解.证明完成.

3 例子

3.1 考虑边值问题：

容易验证：f∞Ψ（1A-11）＞F0Ψ（2A-21）.因此，由定理2.1.1知，当∈（3 843.197 5，4 960.3）边值问题（20）存在正解.

3.2 考虑以下边值问题：

3.3 考虑以下边值问题：

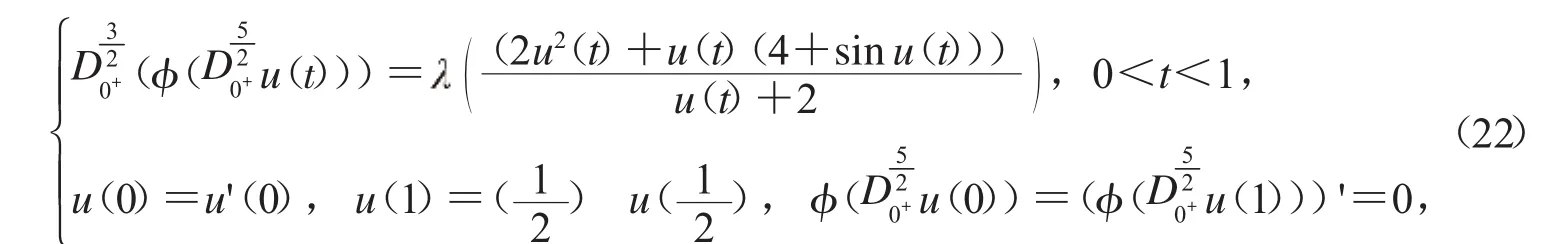
A1≈0.201 6，A2≈0.000 2，F0＝f0＝2，F∞＝10，f∞＝6并且u＜f（u）＜10u，

[1]MILLER K S，ROSS B.An introduction to the fractional calculus and fractional differential equation[M]. New York：Wiley-Interscience，1993.

[2]ROSS B.The fractional calculus and its applications，in：lecture notes in mathematics[M]//Lecture Notes in Mathematics.Berlin-New York：Springer-Verlag，1975.

[3]SAMKOSG，KILBASAA，MARICHEV O I.Fractional integrals and derivatives：theory and applications [M].Yverdon：Gordon and Breach，1993.

[4]KRASONSEL'SKIIMA.Positive solutionsofoperaterequations[M].Gronigen：PNoordhoff Ltd，1964.

[5]OLDHAMKB，SPANIERJ.Thefractionalcalculus[J].MathematicalGazette，1974，56（247）：396-400.

[6]BAI Z，LÜ H.Positive solution for boundary value problem of nonlinear differential equation[J].Journal of Mathematical Analysis&Applications，2005，311（2）：495-505.

[7]ZHAO Y，SUN S，HAN Z，et al.The existence of multiple positive solutions for boundary value problems ofnonlinearfractionaldifferentialequations[J].CommunicationsinNonlinearScience&Numerical Simulation，2011，16（4）：2086-2097.

[8]CHEN T，LIU W，HU Z.A boundary value problem for fractional differential equation with p p math container loading mathjax-Laplacian operator at resonance[J].Nonlinear Analysis Theory Methods& Applications，2012，75（6）：3210-3217.

[9]HAN Z，LU H，ZHANG C.Positive solutions for eigenvalue problems of fractional differential equation with generalized p-Laplacian[J].Applied Mathematics&Computation，2015，257：526-536.

[10]NYAMORADIN.Existenceofsolutions for multi-point boundary value problems for fractional differential equations[J].Arab J Math Sci，2012，18（2）：165-175.

[11]MA D X.Positive solutions of multi-point boundary value problem of fractional differential equation[J]. Arab Journal of Mathematical Sciences，2015，21（2）：225-236.

[12]EL-SHAHEDM.Positivesolutionsforboundaryvalueproblemof nonlinear fractional differential equation [J].Abs Appl Anal，2007，2007：1-8.DOI：10.1155/2007/10368.

[13]WANG H.On the number of positive solutions of nonlinear systems[J].Journal of Mathematical Analysis &Applications，2003，281（1）：287-306.

[14]GUO D J，LAKSHMIKANTHAM V.Nonlinear problem in abstract cones[M].San Diego：AcademicPress，1988.

[15]SUN Y，ZHAO M.Positive solutionsfora classoffractionaldifferentialequations with integral boundary conditions[J].Applied Mathematics Letters，2014，34（1）：17-21.

[16]ZHAOY，SUNS，HANZ，etal.Theexistenceofmultiplepositivesolutionsforboundaryvalueproblems ofnonlinearfractionaldifferentialequations[J].Communications in Nonlinear Science&Numerical Simulation，2011，16（4）：2086-2097.

[17]XU X，JIANG D，YUAN C.Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation[J].Nonlinear Analysis Theory Methods&Applications，2009，71（10）：4676-4688.

[18]AVERY R，HENDERSON J.Two positive fixed points of nonlinear operator on ordered Banach spacea [J].Comm Appl Nonlinear Anal，2001，8（1）：27-36.

[19]BAIL，DAIB.Three solutionsfora p-Laplacian boundaryvalue problem with impulsive effects[J].Appl Math Comput，2011，217（24）：9895-9904.

[20]FENG M.JI D，GE W.Positive solutions for a class of boundary value problem with integral boundary conditions in Banach space[J].J Comput Appl Math，2008，222（2）：351-363.

[21]MA R，ZHANG J，FU S.The method of lower and upper solutions for fourth-order two-point boundary value problems[J].J Math Anal Appl，1997，215（2）：415-422.

Existence of Positive Solution for
Multi-Point Boundary Value Problems of FractionalDifferential Equations with p-Laplacian

ZHANG Yan,MA Dexiang
（College of Mathematics and Physics,North China Universityof Electrical Power,Beijing102206,China）

In the following multi-point boundary value problem of fractional differential equation with p-Laplacian:

fractional differential equation;p-Laplacian operator;multi-point boundary value problem;fixed point theorem

O175.1；O175.8

A

1001-4217（2017）03-0029-13

2016-09-21

张 艳（1991—），女，硕士研究生.研究方向：分数阶微分方程边值问题研究. E-mail：zhuanzhufadai@sohu.com