何惧白璧微瑕

丁毓琪

1 问题背景

在圆锥曲线问题中，“点差法”即代点相减法，对于解决中点弦方程、弦中点轨迹方程以及对称问题等方面都非常有效，堪称利器[1，2].然而，“点差法”有时却会失效，导致错误的答案[3].以笔者所在学校的高二数学月考题为例：

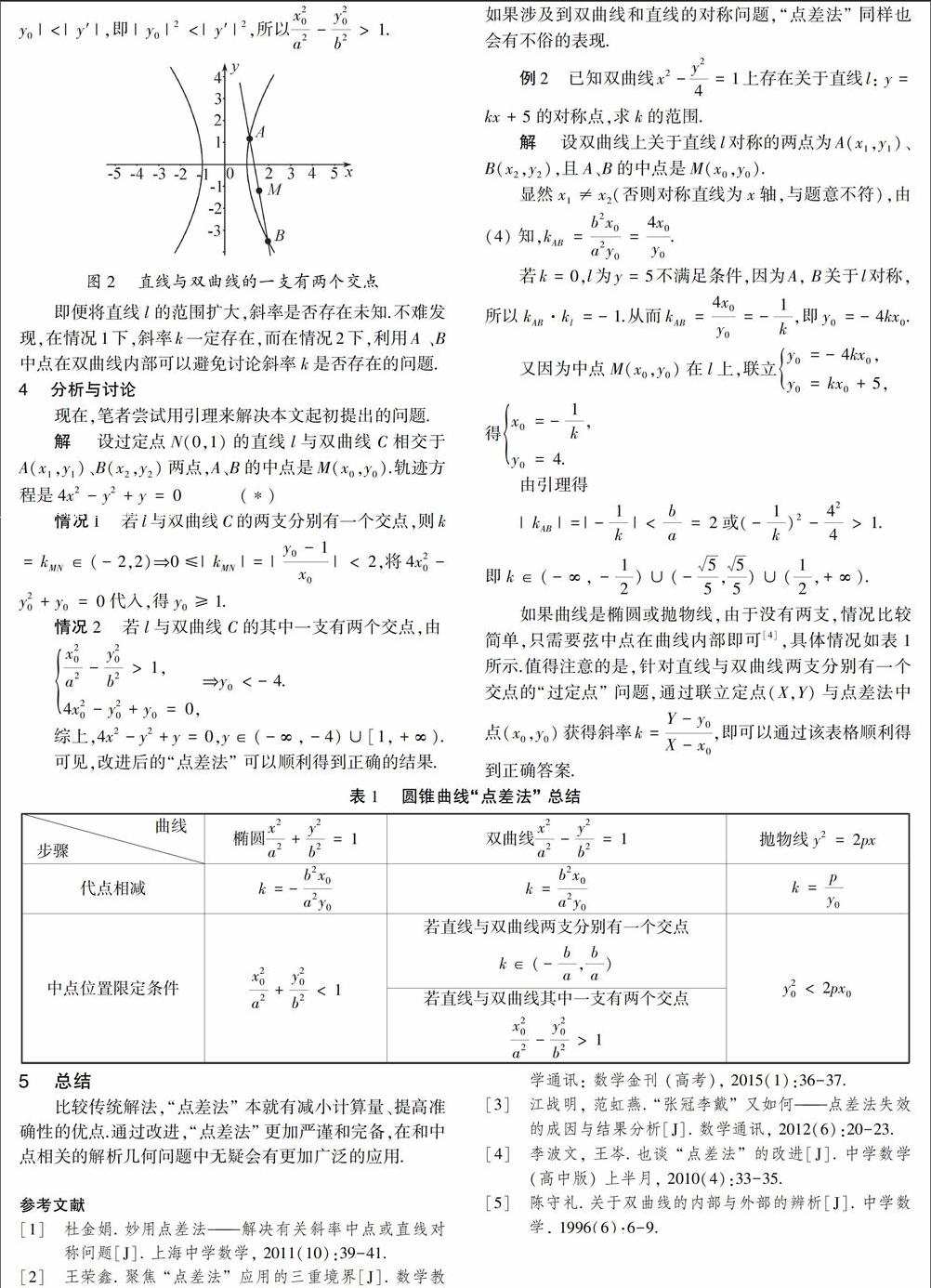
例1 已知直线l经过定点（0，1），被双曲线x2-y24=1所截得的弦的中点轨迹方程是 .

大部分学生由“点差法”可求出轨迹方程，结果是4x2-y2+y=0，但正确答案是4x2-y2+y=0，y∈（-∞，-4）∪[1，+∞）.标准答案给出的做法是联立直线与双曲线法求方程，利用判别式判断直线是否与双曲线有两个交点，再消除参数获得结果.然而，此种做法的计算过程相当繁琐，并且消去参数并不容易.“点差法”求解轨迹方程很方便，但却无法得出正确的取值范围.从而，学生对使用这种方法心存恐惧，让如此有效的方法沦为鸡肋.通过查阅文献，发现虽然有关于改进“点差法”的研究[4]，但是給出的结果对此类“过定点”问题却无能为力.因此，在本文中，笔者试图对“点差法”进行详细的探索以及有效的改进，尤其是讨论了“过定点”问题，使其能够更广泛应用.

2 “点差法”初探

以本题为例，大部分学生可以通过“点差法”得出下面的结果.