历史文化与信息技术交织下“曲边梯形的面积”教学

张灵+刘逸晴+徐章韬

【摘 要】 HPM是中学数学教育研究的热点话题，在深入学科的信息技术的支持下，充分挖掘数学史的教育价值，以更加生动、直观的方式展现历史，从历史中寻找智慧，推动数学教学的开展.本文借助“割圆术”与“曲边梯形的面积”的教学在信息技术下的融合，体会历史文化与现代技术的交织在数学课堂中所产生的重要教学价值，感悟主题研究的重要意义.

【关键词】 数学史；信息技术；数学教育；“割圆术”；曲边梯形的面积

1 引言

近年来数学史具有的重要教育价值受到人们广泛认同，我国颁布的《数学课程标准》，无论义务教育阶段还是普通高中阶段，都有与数学史相关的论述，《全日制义务教育数学课程标准（实验稿）》第 4 部分“课程实施建议”，每一个学段的“教材编写建议”都有“介绍有关的数学背景知识”这一条目.而《普通高中数学课程标准（实验）》认为“数学课程应适当反映数学发展的历史、应用和趋势，……，应帮助学生了解数学在人类文明发展的作用，逐步形成正确的数学观”[1].《数学课程课标》中对数学史的重视是许多专家学者们努力的结果，这些论述表明了教育取向的数学史已从幕后走向台前.

在《数学课程课标》的支持下，如何在实际教学中充分发挥数学史的教育价值是需要考虑和研究的问题.数学教师在教学中难免会遇到这样的情况，有一些历史素材很有教育意义，但是因为缺乏技术支持，却遗憾地不能应用于课堂，或不能更直观地展示出来，这就使得这部分数学史的教育价值被淹没了[2].例如，历史上，多位数学家利用剪拼法证明了勾股定理，但若缺乏信息技术的支持，依赖于“黑板+粉笔”的模式将不能动态直观地展现剪拼法所突出的“剪”和“拼”的过程，也无法突出多种剪拼法之间的区别与联系.

因此，借助信息技术的支持可以使数学史融入数学教育的过程更加生动化、直观化，以充分挖掘其教育意义.历史文化与现代技术跨越时空交织在一起，历史文化使思想更深邃，信息技术使思想更完美.本文以“曲边梯形的面积”教学为例，探讨在信息技术的支持下，如何充分发挥数学史的教育价值.

2 前期分析

在讲授“曲边梯形的面积”这一小节之前，学生已经学习过刘徽“割圆术”的内容，“割圆术”中蕴含的思想方法与求解“曲边梯形的面积”所需的思想方法具有异曲同工之妙.

刘徽是中国古代一位伟大的数学家，他在《九章算术注》中所提出的“割圆术”，巧妙地求解出了圆的面积，并开创了中国古代数学史上圆周率研究的新篇章[3].“割圆术”的核心思想：“以直代曲，无限逼近”，先对圆进行分割，得到若干扇形，随后选择用三角形代替扇形，体现了“以直代曲”.劉徽指出“割之弥细，失之弥少，割之又割以至不可割，则与圆合体而无所失矣”，当分割次数增加至无限多时，由三角形所组成的多边形便与圆完全相和了，这时三角形的面积和等于圆的面积，通过计算便能得到圆的面积的精确值.

“割圆术”中所采用的“以直代曲，无限逼近”的思想、“化整为零、积零成整”的过程以及“分割、近似代替、求和、取极限”的步骤完全适用于求解曲边梯形的面积.在“曲边梯形的面积”教学中，可从历史中寻找智慧，利用刘徽“割圆术”来启发学生思维，让课堂增添历史文化的气氛.

如今信息技术已逐渐走进课堂，从宏观上，信息技术与数学课堂的整合带来教学方式和学习方式的变革；从微观上，信息技术的融入，能够变抽象为具体，化枯燥为生动，突破“黑板+粉笔”静止的二维世界.在信息技术的支持下，数学史能以更为生动具体的形象活跃于数学课堂中.张景中院士指出普适的信息技术不适合直接用于教学，教育信息化活动应能为学科教学服务，“信息技术只有深入学科才能真正发挥作用”[4].数学教学中常用的工具软件有超级画板、几何画板、Mathematica等.教师应能熟练应用这些数学教学中的常用信息技术软件，并根据具体课程内容和数学史料的融入方式选择合适的信息技术.利用几何画板软件可将“割圆术”的过程动态化，并通过数形结合展示“以直代曲、无限逼近”的思想内涵.

3 具体实现

3.1 借助几何画板回顾刘徽“割圆术”的过程

在几何画板中，根据圆的半径，将圆平均分割成若干块，如图1.通过观察扇形的形状，可以得出三角形与扇形的形状最为贴合，选用三角形近似代替扇形，这时存在两种情况：不足近似和过剩近似，如图2.随后增加分割次数，在几何画板中可观察到，随着分割次数增加，不足近似和过剩近似所形成的正多边形的面积越来越接近圆的面积，当分割次数无限次时，便完全重合，如图3，便可求得圆的面积的精确值.回顾了“割圆术”的过程，可在课堂中总结出求解圆面积的四大步骤.

图3评注 在几何画板的支持下，将“割圆术”的过程动态化，可以直观感知到“割圆术”中所展现的逼近过程和蕴含的极限思想.一方面，利用现代技术揭示了中国数学史中的光辉思想，另一方面，通过借鉴历史，启发学生思考如何求解曲边梯形的面积.

3.2 借助几何画板探索“曲边梯形的面积”求解方案

第一步：分割.首先考虑如何对曲边梯形进行分割的问题，在“割圆术”中，刘徽以圆心为出发点，以圆边为终点，将圆按角度平均分割成n个扇形.在特殊曲边梯形中，考虑以某一直边为出发点，以曲边为终点，将特殊曲边梯形分割成n个宽度相等的小曲边梯形，在《几何画板》中做出图4.

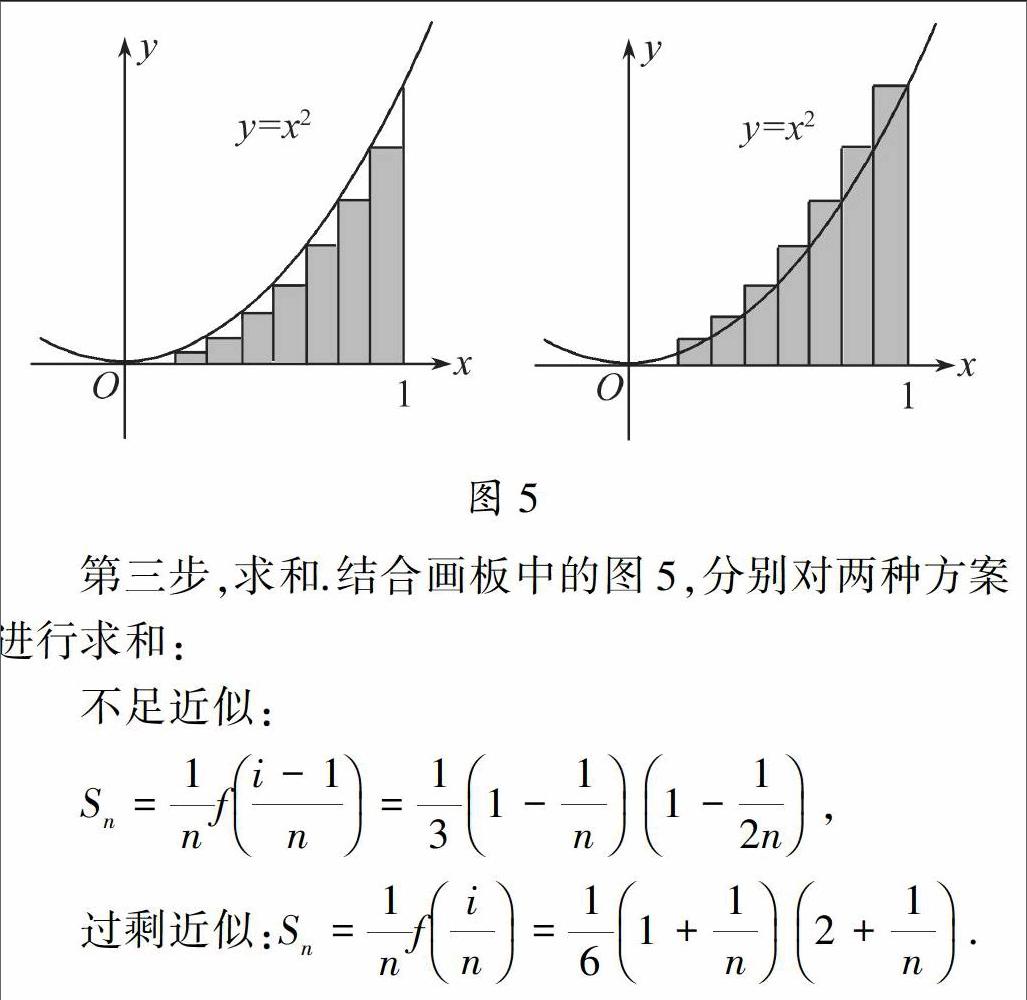
第二步，近似代替.第一步将大曲边梯形分割成了几个小曲边梯形，类比“割圆术”中“以直代曲”的近似代替方案，在特殊曲边梯形中，考虑以矩形代替小曲边梯形，这时，同样存在不足近似和过剩近似两种近似代替方案，如图5.

第三步，求和.结合画板中的图5，分别对两种方案进行求和：

不足近似：

Sn=1nfi-1n=131-1n1-12n，

过剩近似：Sn=1nfin=161+1n2+1n.

第四步：取极限.在几何画板中将分割次数增加，可观察到随着分割次数的增加，两种方案所形成图形的面积都越来越接近曲边梯形的面积，当分割次数无限大时，不足近似和过剩近似所形成图形与曲边梯形相合，如图6.通过取极限，可以得到曲边梯形面积的精确值.

对第三步中两种方案求得的公式进行取极限：

不足近似：

S=Sn=limn→∞131-1n1-12n=13，

过剩近似：

S=Sn=limn→∞161+1n2+1n=13.

得到特殊曲边梯形的面积为13.

评注 类比刘徽“割圆术”，并借助几何画板从“形”上得到了求解特殊曲边梯形面积的过程，再通过计算，从“数”上得到了特殊曲边梯形面积的精确值，数形结合让过程和结果更让人信服.求解曲边梯形面积的過程，既蕴含了从历史中汲取的智慧，又借助了现代技术的支持，将今后要学习的定积分中所包含的思想提前展现的淋漓尽致.

4 感悟

通过对“曲边梯形的面积”教学的分析，可以感受到，信息技术与数学史的结合，不仅能让学生接受数学历史文化的熏陶，而且充分挖掘了数学史中包含的深邃思想和方法，从而推动数学知识的教学.信息技术改变了课程内容的呈现方式，并能深入到课程内容中[2]，在信息技术的支持下，数学知识的历史得以重现，让知识有源可寻，有理可依.在教学中，通过信息技术和数学史的融合，可让学生感受到数学课本知识不只是孤立的已经建好高楼大厦，而是具有自身发展过程的、经过了历史筛选的人类思想的结晶.从感官上，借助信息技术，数学史知识中包含的“数学美”能够得以充分展现，学生能感受到数学并不是公式和数字的堆砌，“数学是可以欣赏的” [2]，并且学生还能够通过亲自操作信息技术融入数学家的思考中，感受数学思想的精妙之处.

信息技术进入课堂已是必然趋势，数学史与信息技术的融合让信息技术不只是工具，还成为了历史文化和思想的载体.重现数学知识历史的功能让信息技术多了一份价值.如何发挥现有材料和工具的最大价值来促进教学是数学教师需要考虑的问题，信息技术和数学史的融合就是一个很好的选择，既能够充分挖掘数学史的教育意义，又可以增添信息技术在数学教学中的价值，在历史文化气氛和现代文明的交织下，思想更加鲜活，知识更加饱满，课堂内容更加丰富，学生的感受也更深刻了.

HPM与信息技术的融合是一个新的研究方向，如何借助信息技术的优势和数学历史知识的文化底蕴来促进数学教学，需要今后更多地探讨和研究.

参考文献

[1] 朱哲，宋乃庆.数学史融入数学课程[J].数学教育学报，2008（4）.

[2] 徐章韬.超级画板的教育价值及其教学应用[M].北京：科学出版社，2015.

[3] 王能超.千古绝技“割圆术”[J].数学的实践与认识，1996（4）.

[3] 张景中，彭翕成.深入数学学科的信息技术[J].数学教育学报，2009（5）.