粒子群结合形态学滤波的滚动轴承故障诊断
王建东,马增强,王梦奇,阮婉莹
(石家庄铁道大学 电气与电子工程学院,石家庄 050000)
滚动轴承零件发生故障时,如内圈、外圈、滚动体表面的麻点、裂纹、剥落等,这些损伤点通过与其他零件反复接触会产生周期性冲击信号。故障早期这些冲击信号比较微弱,且实际情况下振动传输路径复杂,受噪声干扰、多振动源激励和响应、互相耦合等诸多因素影响,滚动轴承早期故障诊断相对困难,探寻行之有效的微弱故障特征提取方法一直是故障诊断领域的热点和难点。
近几年来不少学者对形态学滤波进行了大量研究,文献[1]基于零频到故障特征频率是否出现干扰和冲击特征比值的大小实现了对故障特征频率的提取。文献[2]研究了数学形态学的应用情况。文献[3]对结构元素形状的选取做了合理的说明。文献[4-5]等探讨了数学形态学对机械振动信号的处理。文献[6]对形态学滤波器的设计以及滤波参数的选取规则做了说明。文献[7]利用多尺度的形态学滤波器对滚动轴承故障信号进行特征提取,取得了良好的效果,但在结构元素形状及长度的选取方面没有给出合理的解释。基于上述研究成果,尝试以峭度和故障特征频率能量比值为指标,用粒子群算法对结构元素长度L进行优化,从而得到使故障特征频率能量比值最大的L并将其定义为最优L对信号进行处理,找到故障频率并提取故障特征。
1 粒子群优化算法
在粒子群优化算法中,每个粒子的运动速度受到自己和群体的历史状态信息的影响,从而有机完成整个粒子群在解空间中对最优解的搜索。
1.1 惯性权重
惯性权重能够起到平衡算法的全局和局部搜索能力的作用,是粒子群优化中的重要控制参数,其取值呈现一个递减的过程,从最大值0.9降到0.4。
1.2 学习因子
学习因子反映了算法全局和局部搜索能力,通常取2。
1.3 种群规模
对于粒子群优化算法,种群规模代表着搜寻粒子的规模,规模越大则搜索能力越强,所需时间也相应加长;种群规模过小会造成搜寻信息减少,易陷入局部寻优,本研究中种群规模取值范围为20~30。
1.4 最大飞行速度
飞行速度越大,所涉及的范围越广,搜寻的信息量越大,越容易搜寻到全局最优;飞行速度小,容易在某一区域搜寻而无法跳出,易造成局部寻优,本研究将最大飞行速度设为固定值。
2 形态学滤波
形态学滤波通过设计一个结构元素对待处理信号进行修改或匹配,从而提取信号中的有用成分。形态学滤波效果的好坏主要取决于结构元素的形状和大小。
2.1 基本算子
腐蚀运算的表达式为AΘB={x|B+x⊂A};膨胀运算的表达式为:A⊕B={x|-B+x∩A≠φ};开运算的表达式为:(f·g)(n)=(fΘg⊕g)(n);闭运算的表达式为:(f·g)(n)=(f⊕gΘg)(n)。
2.2 常用形态滤波器
在实际应用中,应根据信号处理目的以及信号的形态特征合理地选择形态算子。在实际的机械故障和轴承故障中,故障信号中往往同时存在正负冲击。单独使用某种形态算子进行滤波往往得不到较为理想的滤波效果,通常使用几种形态算子构成滤波器。最常用的是差值滤波器,其定义式为
fDIF=(f·g)(n)-(f·g)(n)。
2.3 复合评价指标
峭度值是评价信号偏离正常信号的指标,当峭度值较大时只能定性说明较好地提取出了故障信号,却无法定量的找到最优长度。为定量讨论不同结构元素长度对滤波效果的影响,定义故障特征频率能量比值为
式中:fi为频谱图中故障特征频率及其倍频所对应的幅值;fj为所有频率部分对应的幅值;K为频域中信号故障特征频率能量与非故障特征频率能量的比值,其大小反映了故障特征信号在频谱图中所占的比例,K越大,则提取的故障特征效果越好。
本研究选择峭度和故障特征频率能量比值组成评价滤波效果优劣的复合评价指标,即先通过峭度值选择出能较好提取出故障冲击成分的一系列L,再通过粒子群优化算法寻找使得故障特征频率能量比值最大的L并将其定义为最优L。
3 仿真信号分析
3.1 仿真信号设计
为验证本文所述方法的可行性,设计仿真信号x(t)=x1(t)+x2(t)+x3(t)。其中,x1(t)为频率16 Hz的周期性衰减信号;谐波信号x2(t)=cos(40πt)+cos(80πt);x3(t)为信噪比 -10 dB的高斯白噪声。采样点数为2 048个,时间1 s。冲击信号x1(t)的时域图和频谱图如图1所示。

图1 仿真信号的时域图和频域图
x(t)的时域图和频谱图如图1所示。从时域图中可以看出,谐波信号和噪声信号幅值很大,且噪声信号的频率分布于各个频率段中,很难识别出冲击信号x1(t);从频谱图中可以看出,谐波信号的20,40 Hz十分突出,而故障冲击信号却被淹没,很难提取出故障冲击特征。
仿真信号中待提取的冲击特征频率为16 Hz,L的取值范围为1~40(根据经验设置)时,滤波后信号的峭度值如图2所示。从图中可以看出L在1~5或17~22时峭度值较大,可认为较好地提取出了冲击成分,但无法确定L取何值时滤波效果和所提取的冲击成分最明显。

图2 不同L 滤波后的峭度值
根据本文所述方法,以故障特征频率能量比值为目标函数,采用粒子群算法自适应寻优,寻优结果如图3所示。当L取19时,故障特征频率能量比值最大,为1.248 8。因此,综合峭度值和故障特征频率能量比值,判定对信号提取效果最优的滤波器长度L为19。选L为19时的滤波效果如图4所示,从图中可以明显提取出频率为16 Hz的冲击成分及其倍频,且冲击成分幅值明显。
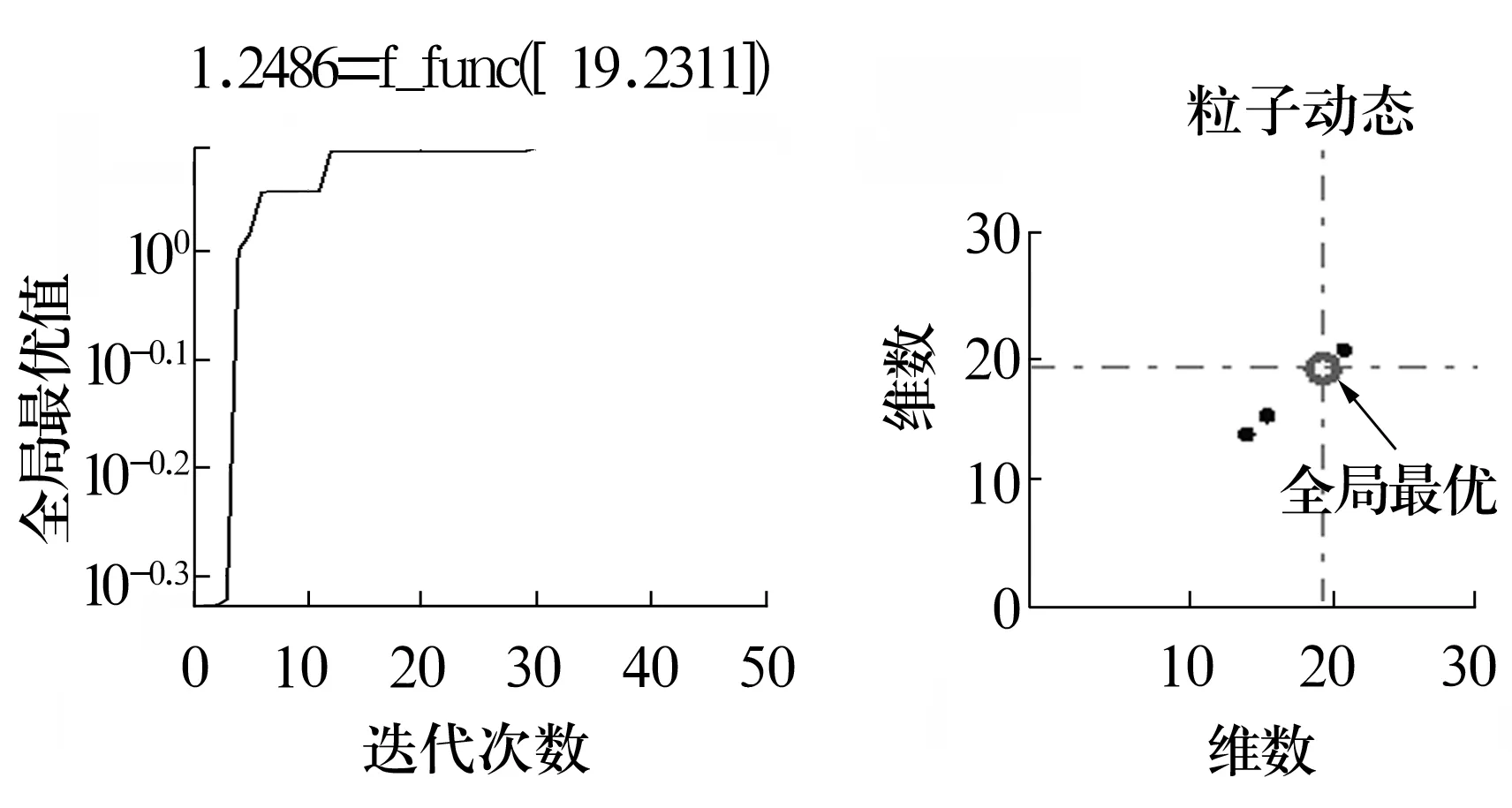
图3 粒子群寻优结果

图4 L为19时滤波后时频图
4 实测信号验证
采用QPZZ-I旋转机械故障试验平台进行试验,信号采样频率为25 600 Hz,试验轴承为N205EM型圆柱滚子轴承,在外滚道上设置高10 mm、宽1 mm的故障基本参数见表1。试验过程中轴承转速为317 r/min,计算得轴承外圈故障频率为28.5 Hz。采样时间共10 s,取较为稳定的振动信号进行分析。

表1 滚动轴承N205EM参数
实测信号的时域图和频谱图如图5所示。从图中可以看出,噪声信号幅值很大,很难识别出故障冲击信号,频率分布没有规律,故障冲击信号被淹没,无法提取出故障冲击特征。

图5 实测信号时域图及频域图
设置L取值范围为1~40,滤波后信号的峭度值如图6所示。根据峭度值初步将L取值范围缩小为5~15,然后以故障特征频率能量比值为目标函数,采用粒子群算法自适应寻优,结果如图7所示,由图可以看出当L取5.8时故障特征频率能量比值最大(0.308 6)。因此,综合峭度值和故障特征频率能量比值,判定对信号提取效果最优的滤波器长度L为6。
L为6时的滤波效果如图8a所示,图中的故障冲击成分突出,提取出了频率为28.5 Hz的冲击成分,且冲击频率处幅值较大,冲击成分明显。对比峭度值最大对应的L=10时的滤波效果(图8b)可知,L=10时得到的故障频率处幅值较大,但除故障频率及其倍频外的其他频率处幅值也明显较大,干扰较为严重。因此认为L=6时提取出的故障冲击特征更清晰、精确。

图6 不同L滤波后的峭度值

图7 粒子群寻优结果图

图8 不同L时滤波后时频图
5 结束语
提出了以峭度值和故障特征频率能量比值组成的复合评价指标来评价滤波效果,并通过仿真信号和实际轴承故障信号进行了验证,结果表明:
1)基于复合评价指标所获得的滤波参数精确度高,提取出的故障频率及其倍频信息更加突出;
2)通过粒子群算法自适应寻找最优参数L,具有实时性好、运算速度快,精确度高等优点;
3)所述方法无需对信号进行预处理,目标函数确定,自适应性较强。

