特定载荷下不同凸度量对数滚子疲劳寿命试验

周立业，陈晓阳，陆锦才

（1.上海大学 机电工程与自动化学院，上海 200072；2.上海和锦滚子科技有限公司，上海 201600）

圆柱滚子轴承应用广泛。目前，我国圆柱滚子轴承的使用寿命远不及发达国家，其中80%的滚子轴承失效是由于滚子破坏。实际使用和试验均表明，圆柱滚子的设计与制造是影响轴承使用寿命的主要因素。其中，滚子凸度设计不合理会导致滚子两端产生“边缘效应”，使滚子过早疲劳失效，致使轴承疲劳寿命大大降低［1］。为消除边缘应力集中，需对滚子进行修形，采用凸度滚子［2］。滚子凸度设计包括凸形设计和凸度量设计［3］，其中凸形研究是凸度设计应用的基础。滚子凸度一般有5种形式，即：直线形、圆弧半凸形、圆弧全凸形、修正线形和对数形。理论研究证明，最佳的滚子凸度轮廓为对数形。

有关对数曲线方程，Lundberg于1939年利用弹性理论的势函数法，设定沿轴线均匀分布、横向按函数s（t）（-1≤t≤1）分布的接触应力，给出了有限长滚子与弹性半空间正接触时圆柱滚子表面修形的素线形状［2］；随后Lundberg又参照Hertz理论进一步简化了滚子素线方程；文献［4］在考虑接触区域长宽比作用的情况下，对Lundberg对数凸形作了进一步修正，并提出一种新的工程对数凸形。基于理论分析，采用超精研技术加工试验滚子的凸形和凸度量，对不同凸度量的对数滚子进行疲劳寿命试验。

文中对特定载荷相同工况条件下不同凸度量的滚子进行完全疲劳寿命试验，分析凸度量对滚子疲劳寿命的影响；并结合一款基于UG软件平台二次开发的滚子轴承接触副受力分析系统［5］，研究了对数滚子理论与实际的最佳凸度设计。

1 试验滚子

试验所选滚子均为Ⅱ级精度，滚子尺寸为φ10 mm×10 mm，有倒角的滚子倒角半径为0.7 mm。

试验滚子对数轮廓形状及滚子外圆的表面粗糙度测量均采用KOSAKA的SEF3500表面粗糙度轮廓测定仪，要求滚子外圆表面粗糙度Ra≤0.04 μm。对于无倒角的直素线滚子，其轮廓如图1所示；有倒角的对数滚子测量点为1.5倍倒角处，即距滚子中心点3.95 mm处，凸度量为9μm的滚子轮廓测量结果如图2所示，该测量（显示）图中x轴放大10倍，z轴放大2000倍。

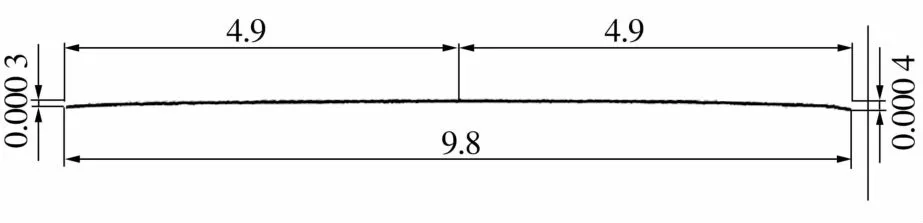
图1 无倒角直素线滚子轮廓Fig.1 Profile of straight generatrix roller without chamfer

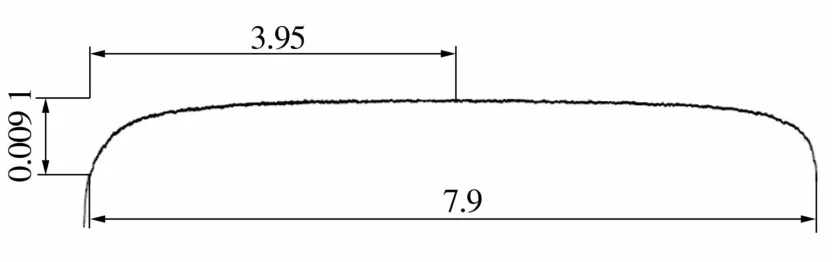
图2 对数滚子轮廓Fig.2 Profile of logarithmic roller

滚子圆度测量采用Taylor圆度仪，选用滚子标准为圆度RONt≤0.6μm，如图3所示，滚子圆度测量结果为0.23μm。

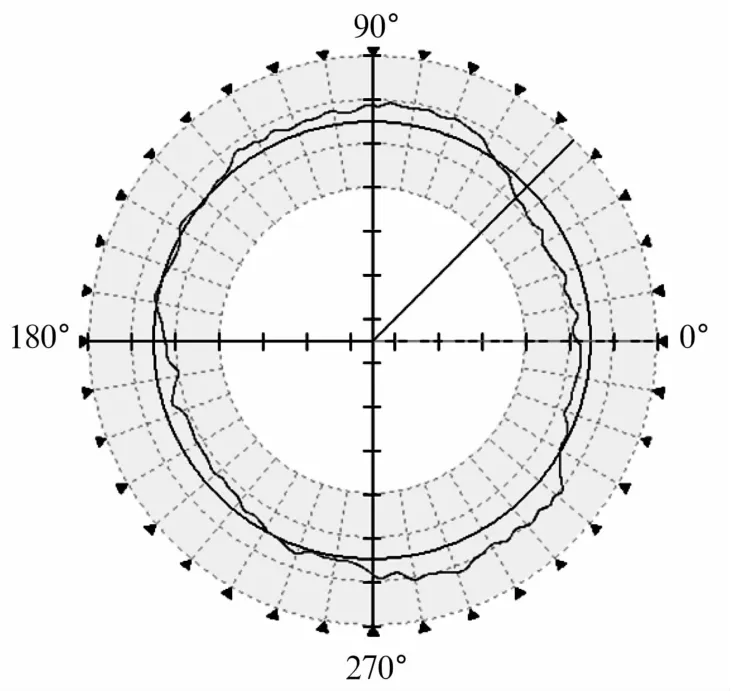
图3 滚子圆度测量Fig.3 Measurement for roundness of roller

为研究特定载荷相同工况条件下，对数滚子的疲劳寿命随不同凸度量的变化规律及其失效特性，根据上述标准选定试验滚子，其滚子凸度几何条件见表1。

表1 试验滚子凸度几何条件Tab.1 Geometrical condition of crowning of test roller

2 试验条件

目前多以整套轴承作为疲劳寿命试验对象，因其失效原因复杂，试验数据对滚子疲劳失效的分析有一定的局限性。因此，采用经过改进优化的四线接触滚子疲劳寿命试验机［6］，该试验机以单个圆柱滚子为对象，高速、重载为目标，可高效、稳定地进行试验，输出结果。

滚子四线摩擦副滚动接触疲劳寿命试验机原理如图4所示，4个陪试滚子（φ16 mm×16 mm，Ⅱ级圆柱直素线滚子）依靠4个主轴精确定位的滚轮支承，试验滚子处于陪试滚子的几何中心，保证滚子四线接触受力均匀。外力通过杠杆原理施加在加载轮上，经陪试滚子传递到试验滚子。试验滚子旋转一周受到4次接触应力相等的循环载荷。试验条件见表2，在该试验条件下试验滚子（凸度量为9μm）为完全润滑，线接触条件下滚子的最大接触应力达到3 GPa。

表2 滚子疲劳寿命试验条件Tab.2 Test conditions of roller fatigue life

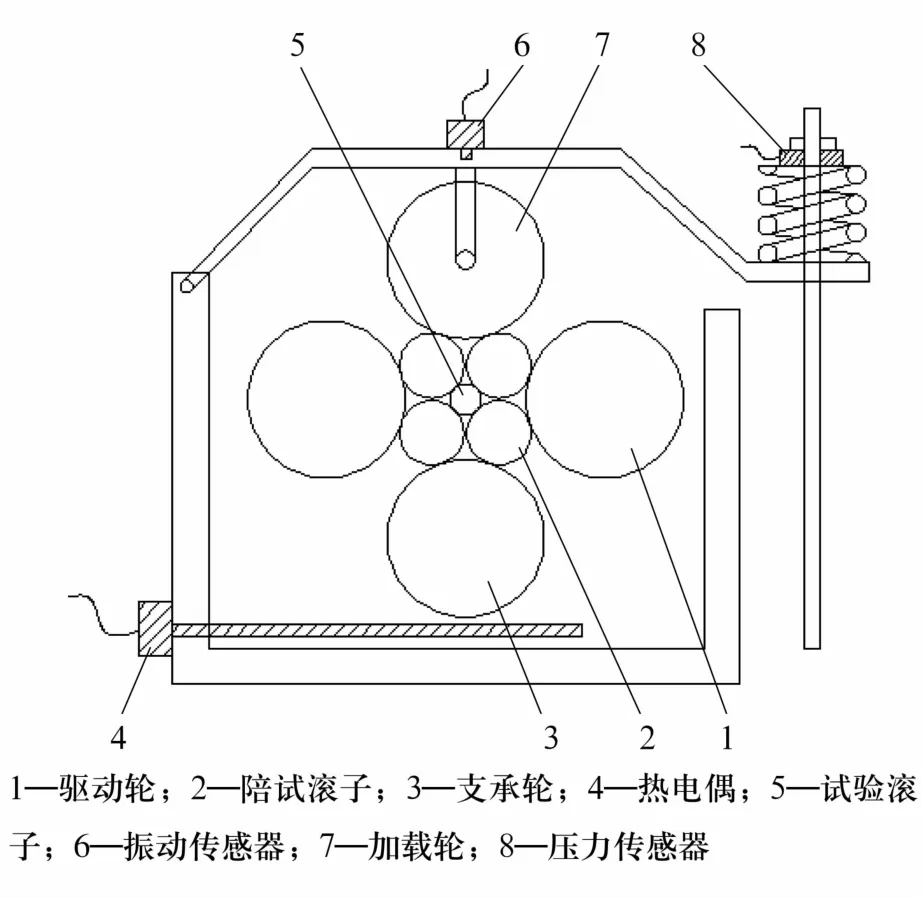
图4 试验机原理图Fig.4 Principle diagram of tester

3 试验结果及分析

由于每种规格试验滚子样本量N＝5＜25，属于小样本，参考GB/T 24607—2009《滚动轴承 寿命可靠性试验及评定》，试验数据为完全样本数据，使用最佳线性不变估计（Best Linear Invariant Estimate，BLIE）方法分析数据，估计Weibull分布的形状参数b和尺度参数ν。完全试验时，

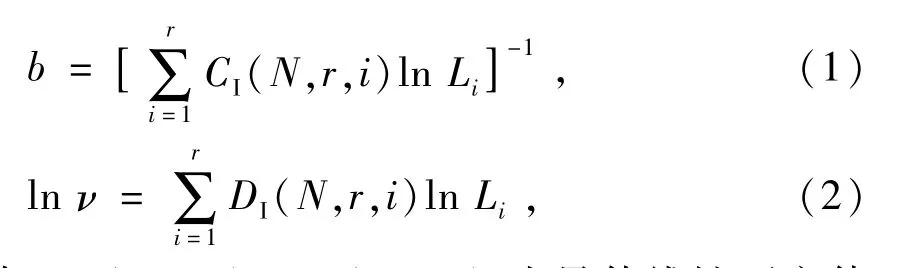
式中：CI（N，r，i），DI（N，r，i）为最佳线性不变估计系数，为常数，可查表得到；N为样本容量；r为轴承失效套数；i为实际寿命由小到大排列的统计量序列；Li第i个轴承的实际寿命。当r＝N时，即为完全样本数据。

各组被试滚子在相同载荷工况下疲劳寿命数据统计及变化趋势如图5所示。根据（2）式可计算出滚子的特征寿命ν，并由Weibull分布参数的估计结果，计算得到滚子的平均寿命以及额定寿命。

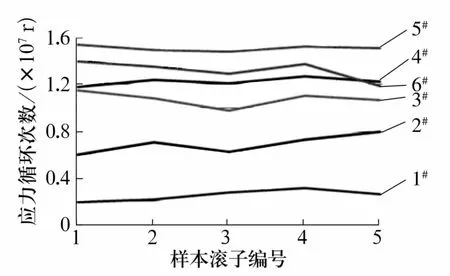
图5 滚子疲劳寿命数据统计及变化趋势Fig.5 Data statistics and variation trend of fatigue life of rollers

基本额定寿命试验值为

中值额定寿命为

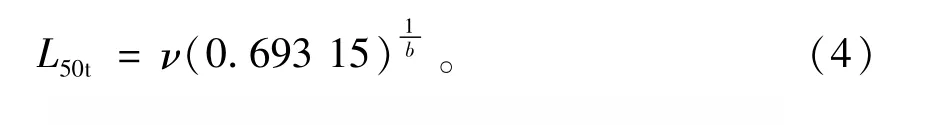
不同凸度量试验滚子的特征寿命、额定寿命和中值寿命计算结果见表3。由表3可知，在特定载荷工况条件下，滚子凸度量对滚子寿命影响很大，且滚子寿命随凸度量的增加而增加，当凸度量大于9μm时，寿命开始下降，表明在所选载荷及凸形、凸量下，最佳凸度量为9μm。

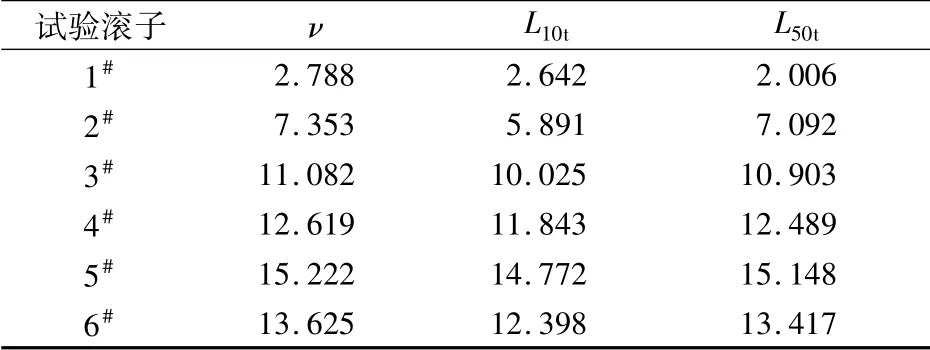
表3 试验滚子寿命数据 Tab.3 Life data of test rollers ×107 r

为进一步模拟分析凸度量对滚子寿命的影响，在UG软件平台上二次开发的滚子轴承受力分析系统中对滚子进行模拟分析，输入参数见表4。

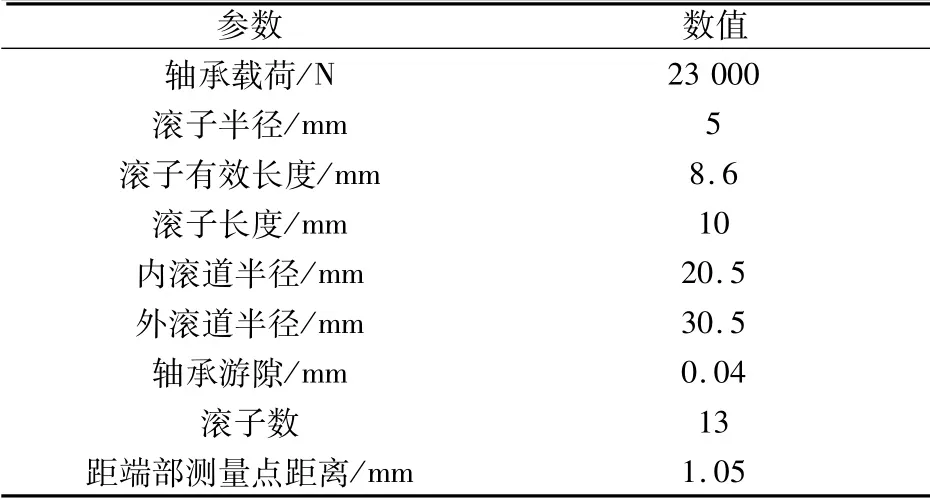
表4 输入参数Tab.4 Input parameters

滚子接触分析显示同时受载滚子数为5，各滚子受载情况见表5。

表5 各滚子受载情况分析Tab.5 Analysis of force on rollers

被测点位置滚子凸度量为：距离对数滚子端部1.050 mm处的凸度量为9.43μm，如图6所示。滚子应力分布如图7所示，受载滚子与内圈最大接触应力为3.05 GPa，与外圈最大接触应力为2.46 GPa。分析结果表明：当轴承载荷为2.3 kN时，滚子最佳凸度量为9μm左右，在该凸度条件下，滚子工作时沿素线方向接触应力分布平滑，可有效延长滚子的疲劳寿命。该结果与试验所得数据相吻合，验证了试验机数据的可靠性和凸度设计方法的合理性。

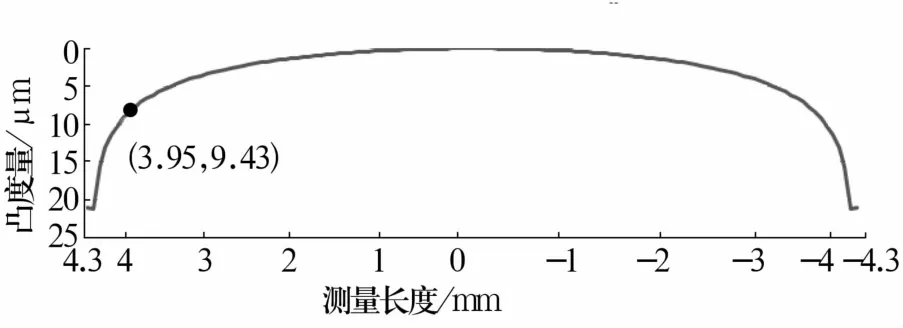
图6 滚子凸度理论曲线Fig.6 Theoretical curve of crowning of roller

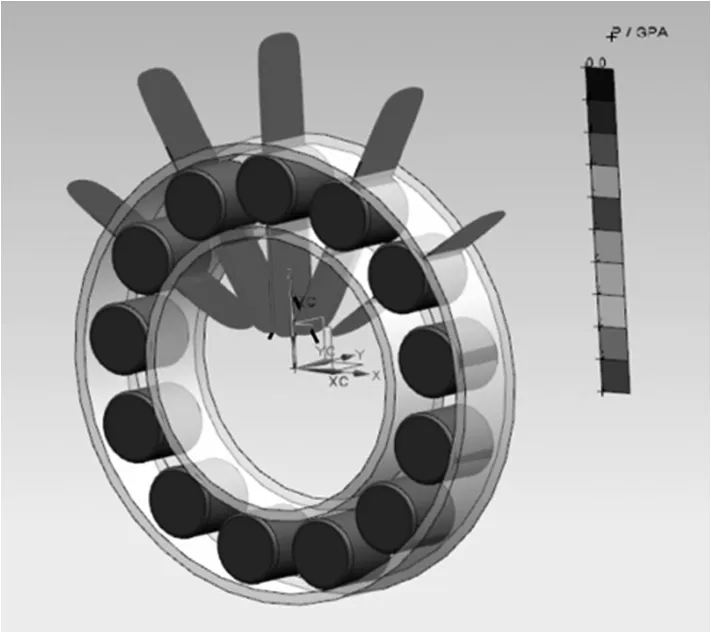
图7 滚子应力分布图Fig.7 Stress distribution diagram of rollers

4 失效滚子表面分析

为研究不同凸度滚子失效部位及其失效机理，对失效滚子最初开始发生疲劳剥落的部位进行电镜扫描，滚子失效部位显微照片如图8所示。

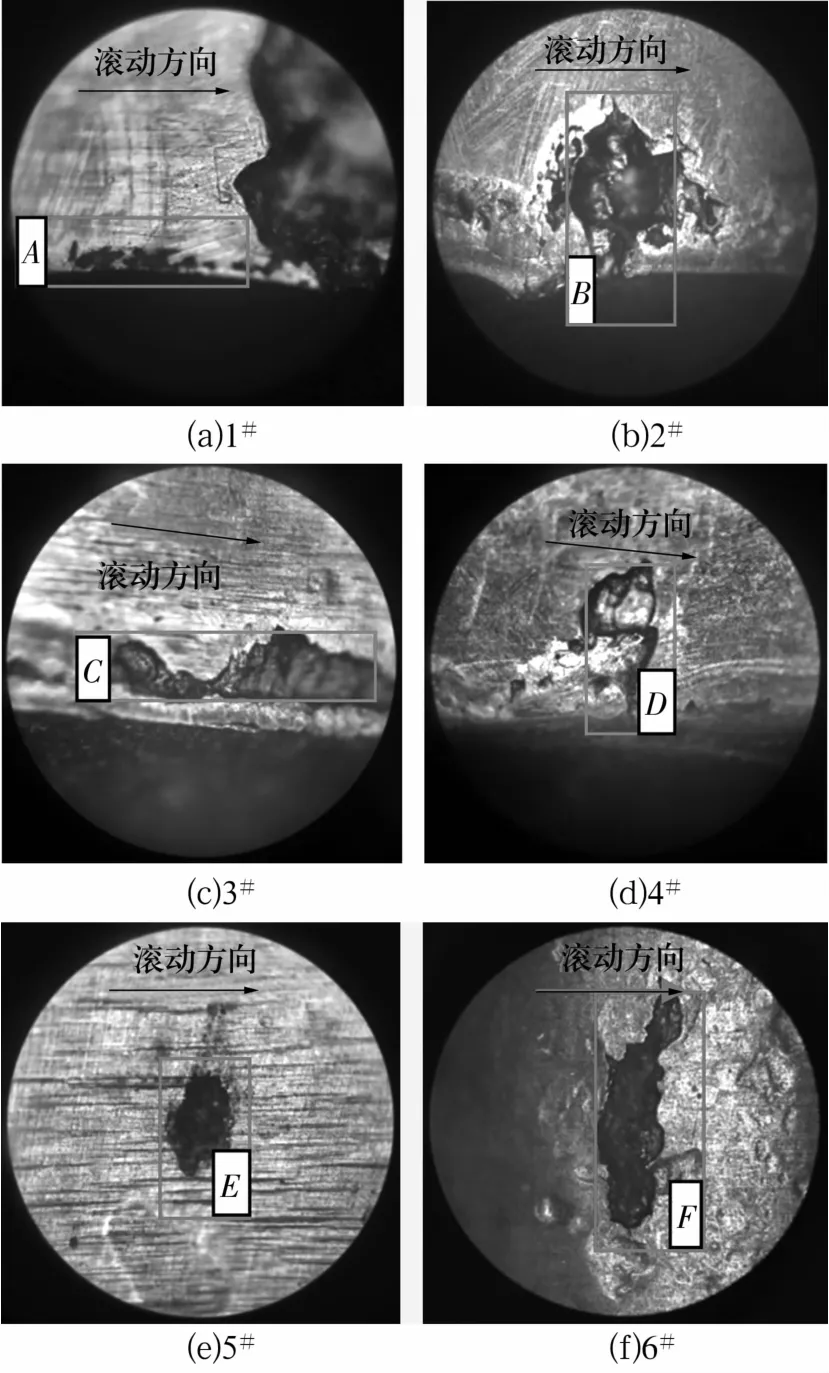
图8 不同凸度被试滚子显微图像（50×）Fig.8 Microscopic images of test roller with different crowning values

由图可知：无倒角直滚子最先在图8a中的A区（滚子边缘）发生失效，进而转化成右侧较大疲劳剥落；有倒角直滚子失效发生在图8b中的B区（倒角与直线段的交接区）；图8c显示发生疲劳失效的C区在距离倒角边0.2 mm位置；图8d显示失效区域D距离倒角边0.6 mm左右；图8e和图8f中滚子失效区域距倒角边均有2～4 mm的距离，倒角周边不再出现剥落。由滚子失效部位分析表明，无凸度直滚子工作时会导致应力集中，产生边缘效应；凸度滚子使滚子端部不再出现疲劳剥落现象，明显改善了滚子边缘应力集中。

为进一步分析滚子失效机理，对试验所用陪试滚子（具有代表性的滚子）进行电镜扫描（图9），分析试验滚子失效部位对应陪试滚子部位的状态。

图9 对应陪试滚子显微图像（50×）Fig.9 Microscopic images of corresponding test roller

由图可知，图9a中陪试滚子G区与无倒角直滚子边缘接触处出现严重裂纹和疲劳剥落；图9b中陪试滚子H区与直滚子倒角接触区域也因部分应力集中而导致产生细小裂纹；图9c和图9d中陪试滚子的I区和J区已经不再出现裂纹和剥落；当试验滚子凸度达到9μm以上时（图9e、图9f），接触区域应力分布相对均匀，接触区域已不存在应力集中现象。

5 结论

结合软件模拟分析和实际试验数据分析得出：

1）实际试验数据验证了滚子受力分析软件对滚子凸度设计的准确性，软件可用于工程对数滚子凸度的优化设计；

2）滚子凸形对接触应力有显著影响，进而影响接触疲劳寿命，其中工程对数素线滚子的接触疲劳寿命较长，对数修形可消除边缘效应和应力集中；

3）特定载荷相同工况条件下存在一个最佳凸度量，工程设计时可根据轴承实际工况来设计滚子最佳凸度，以提高轴承使用寿命。