基于相关峭度准则EEMD及改进形态滤波的轴承故障诊断方法

李翠省，刘永强，廖英英

(石家庄铁道大学 a.机械工程学院；b.土木工程学院， 石家庄 050043 )

滚动轴承运行工况复杂，早期的微弱故障信号常被强噪声严重污染，造成故障特征提取困难，因此，抑制噪声、提取故障特征是轴承故障诊断的研究热点。成熟的小波分析虽然具有多分辨率等优点，但消噪效果很大程度上依赖于阈值和基函数的选择，缺乏自适应性[1-2]；集成经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)[3]能够自适应地将信号从高频到低频逐次分解为具有不同振动模式的IMF分量，近些年来被广泛应用于旋转机械设备的故障诊断中。

EEMD处理后高频部分的IMF分量包含较多的故障冲击成分，但其中仍含有大量噪声，需进一步对IMF分量进行选取、滤波。文献[4]将相关峭度(Correlated Kurtosis，CK)应用于SVD分量的选取中，克服了峭度不能反映特定信号特征的缺点，取得了较好效果。形态滤波可以在滤除噪声的同时最大限度地保留故障信号特征，将形态滤波器用于轴承故障信号的消噪处理[5]，并与EEMD相结合[6]，能够在抑制噪声的同时突出故障冲击成分，在轴承故障诊断中的效果明显。

基于以上研究成果，将相关峭度准则与EEMD及形态滤波相结合，选取经EEMD处理后相关峭度值最大及次大的IMF分量进行重构，并依据相关峭度值最大原则确定形态学结构元素的长度，以更加有效地提取故障信息特征，获得更好的诊断效果。

1 基本原理

1.1 集成经验模态分解

EEMD是针对传统EMD的不足而提出的一种噪声辅助信号处理方法，其通过多次在原信号中加入给定幅值的白噪声并进行EMD处理，从而自适应地将非线性、非平稳信号分解为若干个IMF分量和1个余项r[7]。EEMD利用白噪声频谱的均匀分布统计特性，使不同频带尺度的信号自动映射到合适的参考尺度上，克服了极值点上下包络线的拟合误差，从而有效地避免模态混叠现象，并对多次分解的IMF分量进行叠加求平均处理，达到了消除噪声影响的目的。

1.2 相关峭度

由于机械设备中的冲击源很多，EEMD处理后常会出现与原信号无关的分量，仅采用峭度指标衡量轴承故障成分效果明显不佳。相关峭度[8]同时具备峭度和相关函数的特性，可有效反应振动信号中特定周期脉冲信号强度的参数。轴承故障成分的周期性强，在给定偏移周期的前提下，相关峭度能准确反映感兴趣周期脉冲信号的强度，相关峭度值越大，说明其包含的故障冲击成分越多。

(1)

式中：xn为振动信号；T为感兴趣脉冲信号的周期；N为采样长度；M为偏移周期个数。

1.3 形态滤波器

形态滤波器利用预先设定的结构元素对目标信号进行修正或匹配，很好地保持信号主要形态特征的同时，达到抑制噪声和提取有用信号的目的。形态学滤波包含膨胀、腐蚀、形态闭、形态开4类基本算子[9]，闭运算能够抑制或平滑下方的波谷噪声，开运算能够滤除信号上方的峰值噪声[10]。在实际信号中，往往同时存在正负脉冲，为同时发挥开、闭算子的优势，通常采用形态开、形态闭的级联形式构造均值滤波器对振动信号去噪，即

(2)

2 轴承故障诊断分析

2.1 优选结构元素长度

结构元素的选取对形态滤波效果的影响很大，其形状、尺寸要尽可能接近待分析信号的形态特征。结构元素的选取包含结构元素的形状、高度、长度等。结构元素的形状对滤波效果影响很小[11]，为了便于计算，选取幅值为0的直线形结构元素，结构元素的形状、高度确定后，长度的最优解成为了形态滤波的关键工作[12-13]。

采用相关峭度准则自适应寻求最优结构元素长度的策略，依据相关峭度指标衡量滤波效果，信号经形态滤波后的相关峭度值越大，说明其中冲击成分保留越多，滤波效果越好。设定直线形结构元素长度范围为[2，1倍故障周期长度][12]，结构元素长度从2开始依次增加1个长度间隔直至1倍故障周期长度，计算不同长度所对应的相关峭度值，相关峭度值最大时所对应的结构元素长度即为最优长度，具体流程如图1所示。

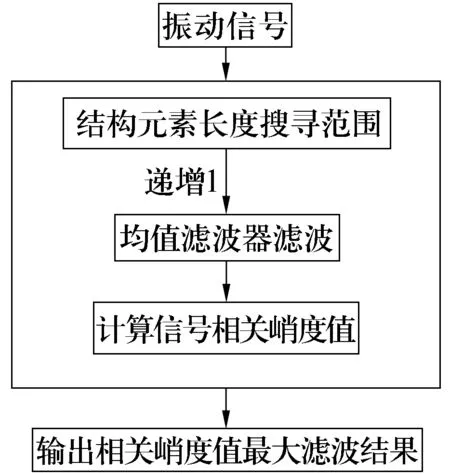
图1 改进形态滤波流程图

2.2 特征提取策略

首先，将振动信号进行EEMD处理，计算各IMF分量的相关峭度值，选取相关峭度值最大及次大的IMF分量进行重构，这样既保留了最多的故障信息,又削弱了强噪声的干扰；然后，对重构信号进行改进的形态滤波处理，进一步抑制噪声，提高故障诊断的精度；最后，将滤波后的信号进行Hilbert包络谱分析。具体流程如图2所示。

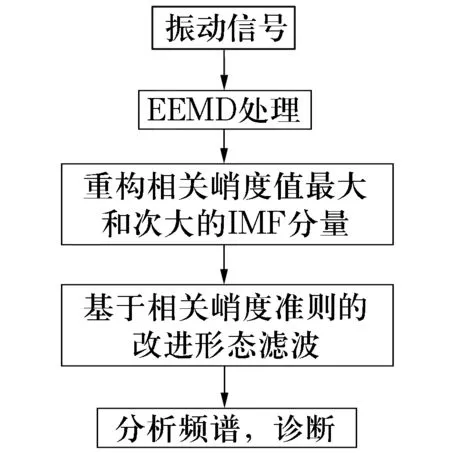
图2 轴承故障特征提取流程

3 试验分析

为验证上述方法的有效性和可行性，在QPZZ-Ⅱ型旋转机械故障试验平台上进行故障模拟试验。试验平台如图3所示，试验轴承为6205-2RS型深沟球轴承，其主要参数见表1。用激光在内圈沟道上切割一个边长0.2 mm、深0.1 mm的正方形凹槽模拟轴承表面损伤类故障，采样频率为10 240 Hz，转速为882 r/min，内圈故障特征频率fi为79.6 Hz。

图3 QPZZ-Ⅱ型旋转机械故障试验台

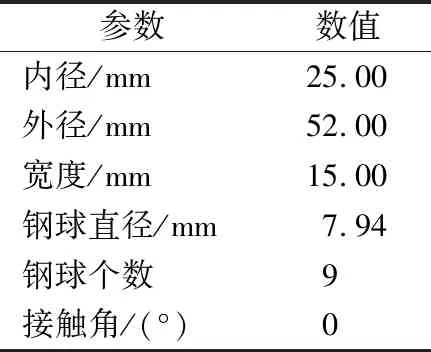
表1 试验轴承的主要参数

以内圈故障为例进行分析，其振动信号的时域和频域图如图4所示，由于强噪声的干扰，从时域图中很难识别故障冲击成分，频域图上亦无法发现故障频率及其倍频。

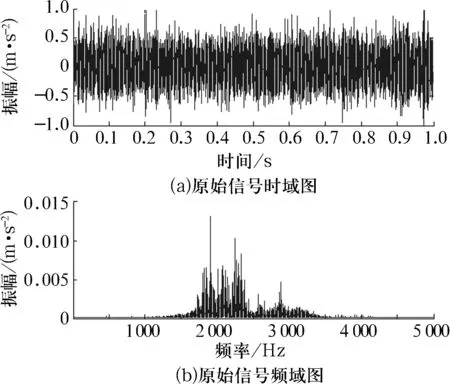
图4 内圈故障信号波形及频谱图

对内圈故障信号进行EEMD处理，分解得到15个IMF分量，其中前3个IMF分量的时域波形如图5所示。取偏移周期数M=5[4]，根据(1)式计算各IMF分量的相关峭度值，分布曲线如图6所示。选取相关峭度值最大的第2个IMF分量及次大的第1个IMF分量进行信号重构，结果如图7a所示，与图4a相比，冲击成分比较突出，但仍可以看到大量噪声，说明EEMD的去噪能力有限。对重构信号进行基于相关峭度准则的改进形态滤波，结果如图7b所示，从该时域图中可以看到明显的冲击成分，说明该方法能够有效地抑制噪声。

图5 内圈故障前3个IMF分量

分别对原始信号、重构信号及重构后滤波信号进行处理，得到的Hilbert包络谱如图8所示。从图中可以看出：原始信号中只能看到内圈故障特征频率(79.09 Hz，接近内圈理论故障特征频率79.6 Hz)，且周围存在较强的干扰；重构信号中的1倍频比较突出，2倍频谱线勉强可以找到，整体解调效果不佳；重构后滤波信号中可清晰地看到转频 (14.69 Hz，接近转频理论值14.7 Hz)，故障特征频率79.09 Hz、2倍频158.2 Hz和3倍频238.8 Hz，谱线都很突出，而且包络谱中以各阶倍频为中心在其两旁有间隔等于转频的调制谱线，综合分析可诊断为内圈故障，也验证了该方法的正确性和有效性。

图7 重构信号滤波前、后时域图

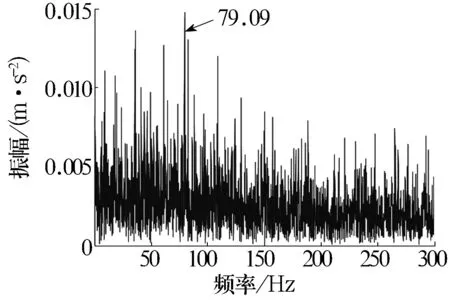
(a)原始信号

(b)重构信号

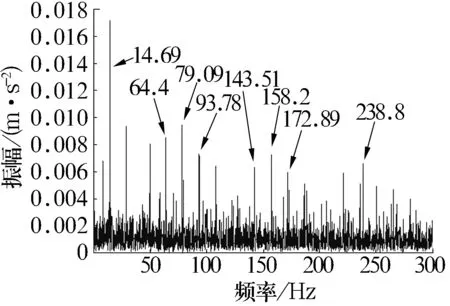
(c)重构后滤波信号

4 结束语

针对轴承故障特征信息易被噪声污染的特点，提出了一种基于EEMD和形态滤波相结合的轴承故障诊断方法。将相关峭度应用于IMF分量的选取，能更加有效地提取微弱故障信息；基于相关峭度值最大原则的形态学滤波器可自适应地确定结构元素长度，克服了传统形态滤波器结构元素长度选取的任意性和经验性，能最大限度地保留故障冲击成，实现最优滤波；EEMD与形态滤波相结合，充分发挥各自优势，使得该方法滤波能力强、故障特征提取精度高，且易于实现，更适用于轴承的精确故障诊断。