一个相同的式子，三个不同的结论

刘红霞

【摘要】 新课程标准下的高中数学教材内容新颖，知识丰富，每一道例题的安排，习题的设置，都凝聚着无数教育专家的智慧，具有深刻的思想性，广泛的应用性，严谨的逻辑性。因此，深入挖掘教材习题，发挥内在潜能，非常有利于培养学生思维的深刻性、广阔性与创造性。同时，教材中的习题还具有广范性，典型性和探究性，是课本的精髓。

【關键词】 高中数学 习题教学

【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711（2017）05-146-01

0

高中数学课本（选修（2-1））（北师版）中有这样两道题：①ΔABC两个顶点A、B的人材分别是（-6，0）、（6，0），边AC 、BC 所在直线的斜率之积等于，求顶点C 的轨迹方程（课本第70页）。②已知椭圆，求以点P（2，-1）为中点的弦所在的直线方程（课本第96页）。关于这两道习题的求解过程及正确答案，无论是初学者、还是高三学生都已不是问题。可是，你是否真正掌握了这两道习题的作用呢？下面就将这两道习题拓展开吧！

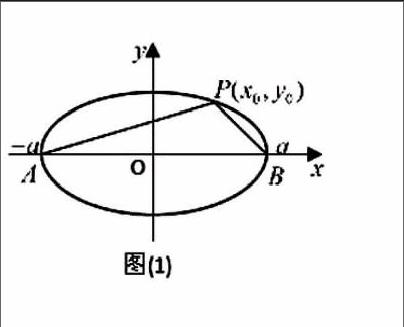
拓展一：A、B是椭圆，长轴的两端点，P是椭圆上除A、B外的任意一点，设直线PA 的斜率为k1，直线PB 的斜率为k2，求k1·k2=-b21a2

解：设p（x0，y0） （其中y0≠0 ），由题意知A（-a，0） ，B（a，0） ，则k1=y01x0+a，k2=y01x0-a

∴k1 · k2 = -y20 1x20 -a2

又∵x21 1a2 + y21 1b2 = 1（a > 0，b > 0）

∴y20 = b2（1-x20 1a2） = b2（a2-x20 ）1a2∴k1·k2=-b21a2

拓展二：如图（2），已知斜率为k1的直线l与椭圆x21a2+y21b2=1（a>0，b>0）相交于A、B两点，弦AB 的中点P与椭圆中心O的连线斜率为k2，则k1·k2=-b21a2

设A（x1，y1）、B（x2，y2） 则P（x1+x212，y1+y212）

∴k1=y1-y21x1-x2， k2=y1+y21x1+x2

k1 · k2 = y21 -y22 1x21 -x22

又∵ A（x1，y1） 、B（x2，y1）在椭圆上

∴x21 1a2 + y21 1b2 = 1 ①

x22 1a2 + y22 1b2 = 1②

①-②得x21 -x22 1a2 + y21 -y22 1b2 = 0x21 -x22 1a2 = -y21 -y22 1b2

∴y21 -y22 1x21 -x22 = -b21a2即k1·k2=-b21a2

拓展三：已知A、B是椭圆x21a2+y21b2=1（a>0，b>0）上点关于原点对称的两点，点M是椭圆上与A、B不重合的一点，若直线MA的斜率为k1，直线MB 的斜率为k2，则k1·k2=-b21a2（证明略）

拓展四：根据上面椭圆中的三个拓展性质，类比地研究双曲线中，对应的有关结论：

①已知A、B是双曲线x21a2-y21b2=1（a>0，b>0）的实轴两端点，P是双曲线上除A、B外的一点，若直线PA 的斜率为k1，直线PB 的斜率为k2，则k1·k2=b21a2

②已知斜率为k1的直线l与双曲线x21a2-y21b2=1（a>0，b>0）相交于A、B两点，弦AB的中点P与双曲线中心O的连线斜率为k2，则k1·k2=b21a2

③已知A、B是双曲线x21a2-y21b2=1（a>0，b>0）上关于原点对称的两点，点M是曲线上异于A、B的一点，若直线MA的斜率为k1，直线MB 的斜率为k2 ，则k1·k2=b21a2

对于形如x21m2-y21n2=1的曲线，都是成立的。

拓展五：拓展一、二、三、中的结论，不仅在椭圆、双曲线中成立，在圆中也是成立的，只要是形如x21m+y21n=1的曲线中，都有k1·k2=-n1m，也就是说：通过以上的推导证明，大家应该注意在学习数学的过程中，不应该仅局限于算出问题的答案，我们要学会对问题的变疑，推广与拓展，只有这样，我们才能真正地理解数学中的每一个知识点，撑握课本中的每一道习题。

下面提供几道练习题，供大家小试牛刀：

①已知椭圆4x2+y2=1 ，若直线y=x+m 被椭圆所截得的弦的中点在直线x=-113 上时，求直线方程；

②已知M（4，2）是直线l被椭圆x2+4y2=36 所截得的线段AB的中点，求直线l的方程；

③过椭圆C ：x21a2+y21b2=1（a>0，b>0） 上一点M作直线MA、MB 交椭圆于A、B两点，且点A、B关于原点对称，设MA 、MB 的斜率分别为k1、k2，k1·k2=-213 又椭圆的一个焦点与抛物线y2=4x 的焦点重合，求该椭圆方程。

[ 参 考 文 献 ]

[1]赵国瑞.不同的图形相同的结论——“M”型图和“U”型图角之间的关系[J].语数外学习：初中版七年级，2011（3）：31-32.

[2]宋庆.一个问题的简单解答[J].中学数学，2002（11）：10.

[3]刘超.凸四边形的一个面积公式——“类海伦公式”[J].数学通讯，2010（5）：41-42.