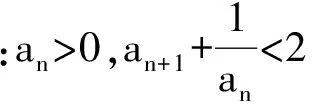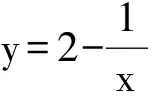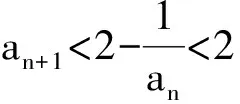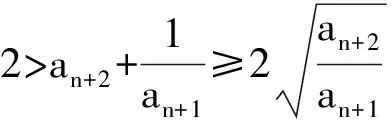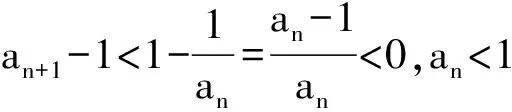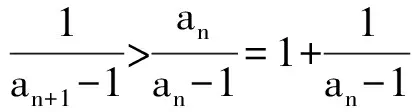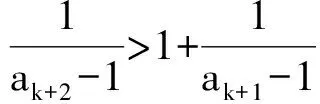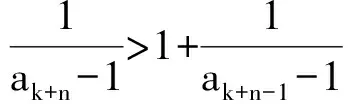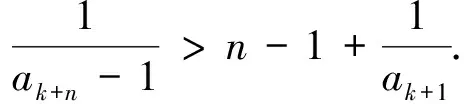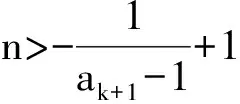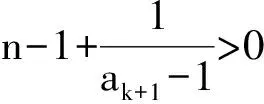用蛛网巧释浙江数列压轴题*
●孙军波
(温岭中学,浙江 温岭 317500)
用蛛网巧释浙江数列压轴题*
●孙军波
(温岭中学,浙江 温岭 317500)
借助蛛网工作法,从图像角度形象地诠释了2017年浙江省数学高考压轴题,并借助图像进行推广延伸.文章通过数形结合简议了对于这一类迭代数列的处理和命制思路,为解决和编制这一类型问题提供方向和思路.
蛛网工作法;不动点;数形结合;数列不等式
2017年浙江省数学高考仍以数列题压轴.数列作为刻画离散模型的重要函数,在高考中常与不等式相结合,这也是困扰学生的难题.笔者以2017年浙江省数学高考压轴题为例,引入“蛛网法”,通过数形结合简议这一类型数列的收敛、发散变化,希望能给大家带来一些启发与帮助.
1 考题再现
例1 已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(其中n∈N*),证明:当n∈N*时,
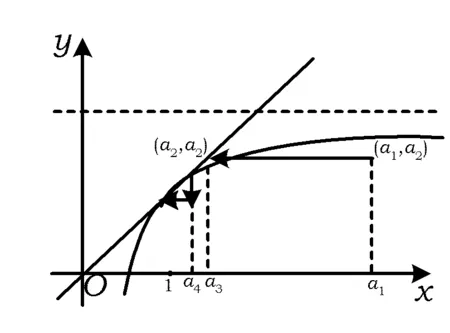
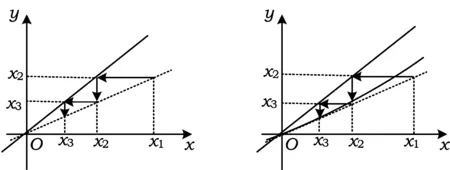
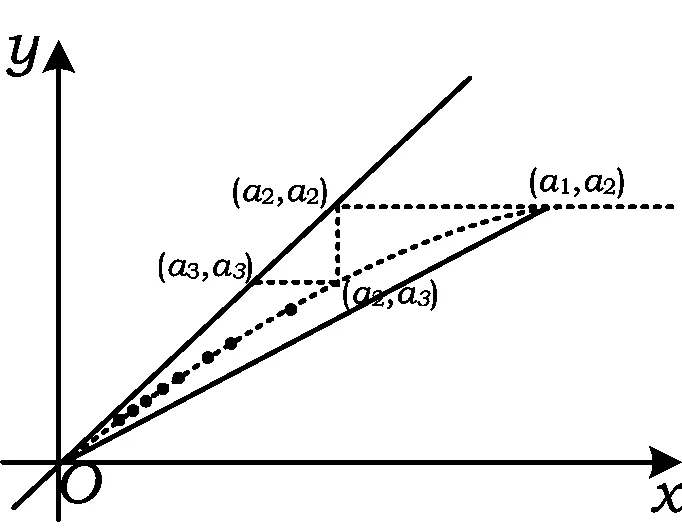
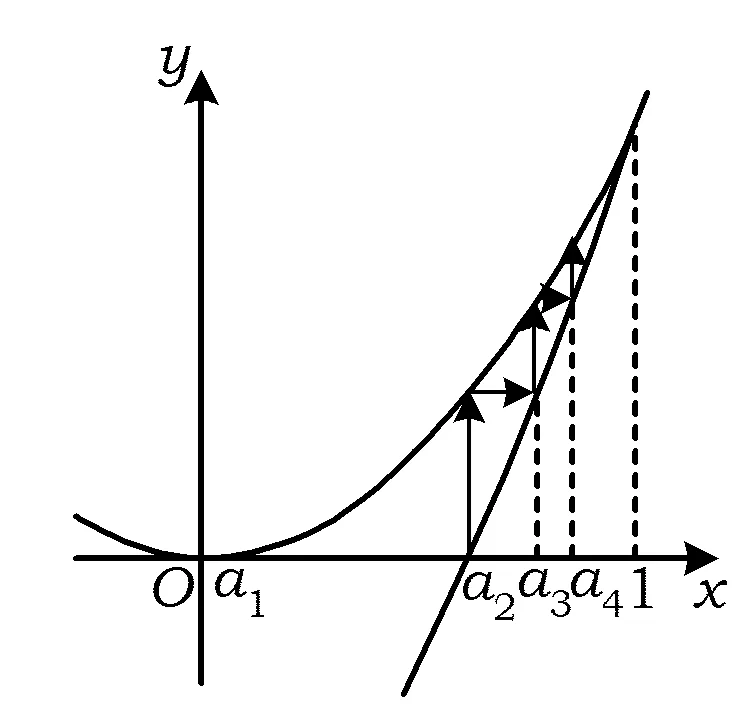
1) 0 (2017年浙江省数学高考试题第22题) 即 第3)小题是在第1),2)小题基础上的引申.若仅仅停留在就题解题,则不能使学生的数学能力得到提升.笔者将其和近几年的一些高考题作了比较归纳,认为关注数列的收敛和发散可能是解决这一系列不等式的关键之处.借助图像可以直观地看透这类数列的变化. 从曲线的观点,点(xn,xn+1)在曲线x=y+ln(1+y)上,按如下步骤作图:第1步作点(x1,x2),第2步过点(x1,x2)作平行于x轴的直线交y=x于(x2,x2),第3步过点(x2,x2)作平行于y轴的直线交曲线x=y+ln(1+y)于(x2,x3),依次类推…… 图1 图2 上述方法有一个很形象的名称——蛛网工作法[1].对于an+1=f(an)(其中n∈N*)迭代生成数列的具体情况,往往不需要作很多计算,通过图像观察即可.此类数列变化主要有以下两个规律: 命题1的证明略. 命题2 设数列{an}满足递推公式an+1=f(an),其中n∈N*,函数f在区间I上单调,同时数列{an}的每一项都在区间I中,则只有两种可能:1)当f单调增加时,{an}为单调数列;2)当f单调减少时,{an}的两个子列{a2k-1}和{a2k}均为单调数列,且具有相反的单调性. 分析 1)若f(x)在区间I上单调增加,假设a1 ak+2-ak+1=f(ak+1)-f(ak)>0. 若a1≥a2,同理用数学归纳法可证明an≥an+1. 2)可类比上述结论1)的证明过程. 根据命题2可作出如图3和图4所示的图像. 图3 图4 严格证明这两个命题需要用到数学归纳法等,以上的几何观察在发现规律、提供思路和命题时是很有用的. 借助图像,可以清晰地看出数列{xn}的变化,根据图1和图2,例1可作如下改编: 改编1 将x1=1改为x1>0,数列{xn}单调递减且收敛于0,则结论1),2)仍然成立,只是影响结论3)的结构形式. 改编2 将x1=1改为x1=-1,数列{xn}单调递增且收敛于0,即 1)xn 改编3 将条件改为xn=xn+1+ln(1+xn+1)(其中n∈N*),xn+1 改编4 将条件改为x1=1,xn=xn+1+ln(1+kxn+1)(其中k>1,n∈N*),结论1),2)仍然成立. 根据图像,可以多角度清晰地去改编例1,其中曲线的变化和首项的范围是影响数列收敛、发散的关键. 回顾近几年的数学高考数列试题,均可用蛛网法解释. (2015年浙江省数学高考理科试题第22题) 图5 分析 利用蛛网可以发现:点(an,an+1)在函数y=f(x)=x-x2上,借助不动点,按如下步骤作图:第1步作点(a1,a2),第2步过点(a1,a2)作平行于x轴的直线交y=x于(a2,a2),第3步过点(a2,a2)作平行于y轴的直线交y=f(x)于点(a2,a3),依次类推……(如图5). 1)an 2)Sn>n-2; 3)Tn<3. (2008年浙江省数学高考理科试题第22题) 图6 (2014年重庆市数学高考理科试题第22题) 图7 借助数形结合,可以看清此类迭代数列不等式的问题,也可以去命制此类数列问题,还可以去解决一些递推关系为不等式的问题.笔者曾命制过一道地区高考模拟试题如下: 1)求证:an+2 2)求证:an>1. 图8 因为 所以 an+2 2)假设存在ak≤1(其中k≥1,k∈N*),由第1)小题可得当n>k时,an≤ak+1≤1. 于是 … (1) 因此 这显然与式(1)矛盾.故an>1(其中n∈N*). [1] 谢惠民,恽自求,易法槐,等.数学分析习题课讲义(上册)[M].北京:高等教育出版社,2003. �2017-06-14; 2017-07-03 孙军波(1982-),男,浙江温岭人,中学高级教师,教育硕士研究生.研究方向:数学教育. O122 A 1003-6407(2017)08-48-03
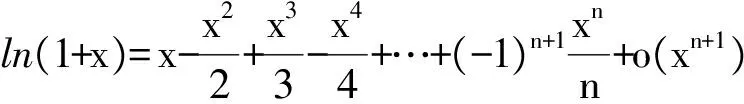
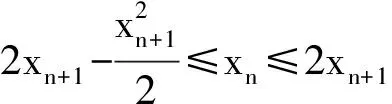
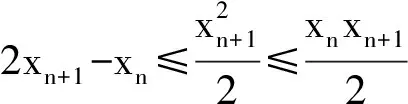
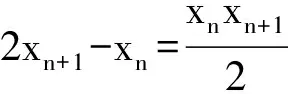
2 方法溯源
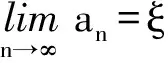
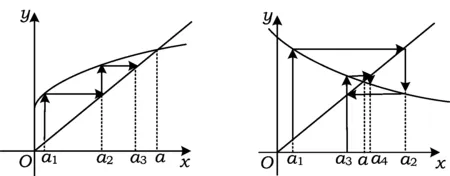
3 题目改编

4 经典回顾
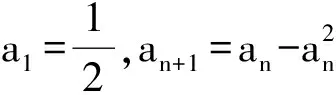
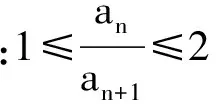
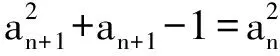
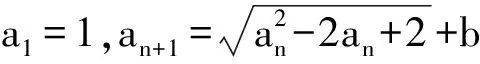
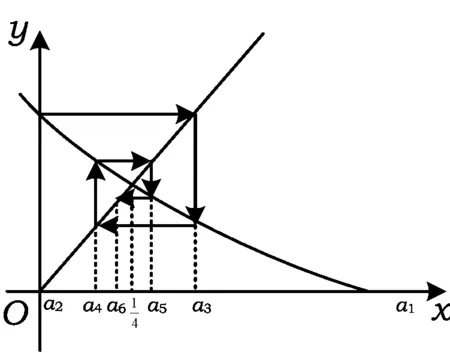
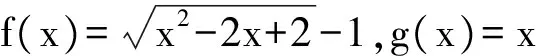
5 问题拓展