求解旅行商路径规划问题的改进模拟退火算法

周 君，贾昆霖

(1.惠州工程技术学校 教务工作部，广东 惠州 516001；2. 广东省惠州商贸旅游高级职业技术学校 培训中心，广东 惠州 516000)



求解旅行商路径规划问题的改进模拟退火算法

周 君1，贾昆霖2

(1.惠州工程技术学校 教务工作部，广东 惠州 516001；2. 广东省惠州商贸旅游高级职业技术学校 培训中心，广东 惠州 516000)

旅行商路径规划问题(GTSP)是一个典型的NP完全问题。文中针对这一困难问题，改进了能够求解GTSP问题的传统模拟退火算法，这样的做法回避了传统算法的一些缺点。具体而言，GTSP问题可以转化为多段映射问题，而动态规划算法可解决这一问题，同时还大幅缩短了整个算法的运行时间。大量实验结果证明，改进的模拟退火算法能够在更短的时间内收敛，并可得到比传统模拟退火算法质量更好的最优解。

模拟退火算法；动态规划算法；旅行商路径规划问题；目标函数

旅行商路径规划问题(GTSP)通常被称为旅行商问题、旅行推销商问题或者货郎担问题，其是最基本的路径规划问题。求解GTSP问题等价于在完全图中找到具有最短路径的哈密顿回路，这是一个典型的组合优化NP困难问题。研究人员已提出了诸多算法来解决这一问题[1-3]，尽管这些方法可得到近似的最优解，但算法只能用于点较少的图，且计算时间较长。所以，本文改进了传统模拟退火算法，该种改进的算法可以在有限的时间内得到全局最优解。

模拟退火算法是上世纪80年代初学界提出的求解NP完全问题的智能算法[4]，该算法可以从局部最优解中概率性地跳出，最终得到全局最优解[5]。本文在这一传统模拟退火算法的基础上，分析了其原理与不足，并提出了一种改进的模拟退火算法。文中GTSP问题被转化为能够使用动态规划算法来解决的多段映射问题。此外，为了防止在跳出局部最优解时丢掉全局最优解，本文在该算法运行过程中增加了记忆功能，将当前最优解记录下来。实验结果表明，与传统模拟退火算法相比，改进后的算法具有更快的收敛速度，其框架和全局最优解的性质也大幅提高。

1 问题描述

用图论的表示方法，GTSP问题可以被定义为：G=(V,A)是一个加权有向图，其中V={v1,v2,…,vn}是顶点的集合，A={(vi,vj),i≠j,vi,vj∈V}是顶点之间有方向的线的集合[6]。

TSP问题是在一个加权图中找到经过所有点的哈密顿回路的最短路径，这一最短路径的起点与终点必须相连接。TSP问题可以被认为是GTSP问题的特例。在GTSP问题中，顶点集合V被分为m个子集合V1,…,Vm且V1∪…Vm=V，求解也同样需要找到经过所有的点的哈密顿回路的最短路径。若将问题求解的区域简化为一个城市，则GTSP问题就简化成为一个TSP问题，所以GTSP问题显然是一个NP完全问题[7-9]。

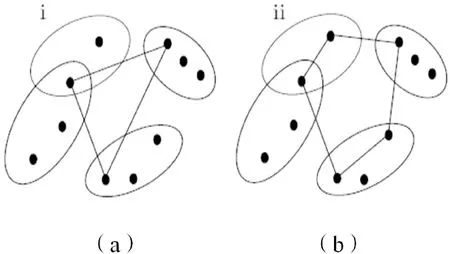
图1 GTSP问题举例

GTSP问题有两种类型：第一种要求每个集合中仅有一个点可以被访问，如图1(a)所示；第二种要求每个集合内至少有一个点可被访问，如图1(b)所示。本文研究的就是第一种情况。

2 改进的模拟退火算法

2.1 具体解决方案的编码设计

对于NP困难优化路径问题，求解时间将以指数级的速度增长，最终时间过长而不能被解决。所以，人们开始通过启发式搜索算法来寻求令人满意的结果。为了将GTSP问题转化成为多段映射问题，每个点均用整数来编码。n个点分别使用整数1,2,…,n来表示，且分别加上起点和终点。这两个点分别用整数0和n+1表示，其到相邻的点的距离定为1。一个完整的方案可表示为(0,x1,x2,…,xn,m+1)，1≤xi≤n，xi≠xj，其中，xi是第i个点的号码[10-12]。

将方案编码后，求解GTSP问题可被转化为多级图的最短路径问题。图2展示了一个完整的解决方案(0,x1,x2,x3,4)，该方案有3个点群，x1=[x10,x11,x12]、x=[x20,x21,x22]、x3=[x30,x31]。在图中，数字0表示起点 ，数字4表示终点t，多级图最短路径问题就是找到终点t到起点s的最短路径。在图2中，使用粗实线画出了最短路径，在这一多级图中的每个阶段中有且仅有一个点。

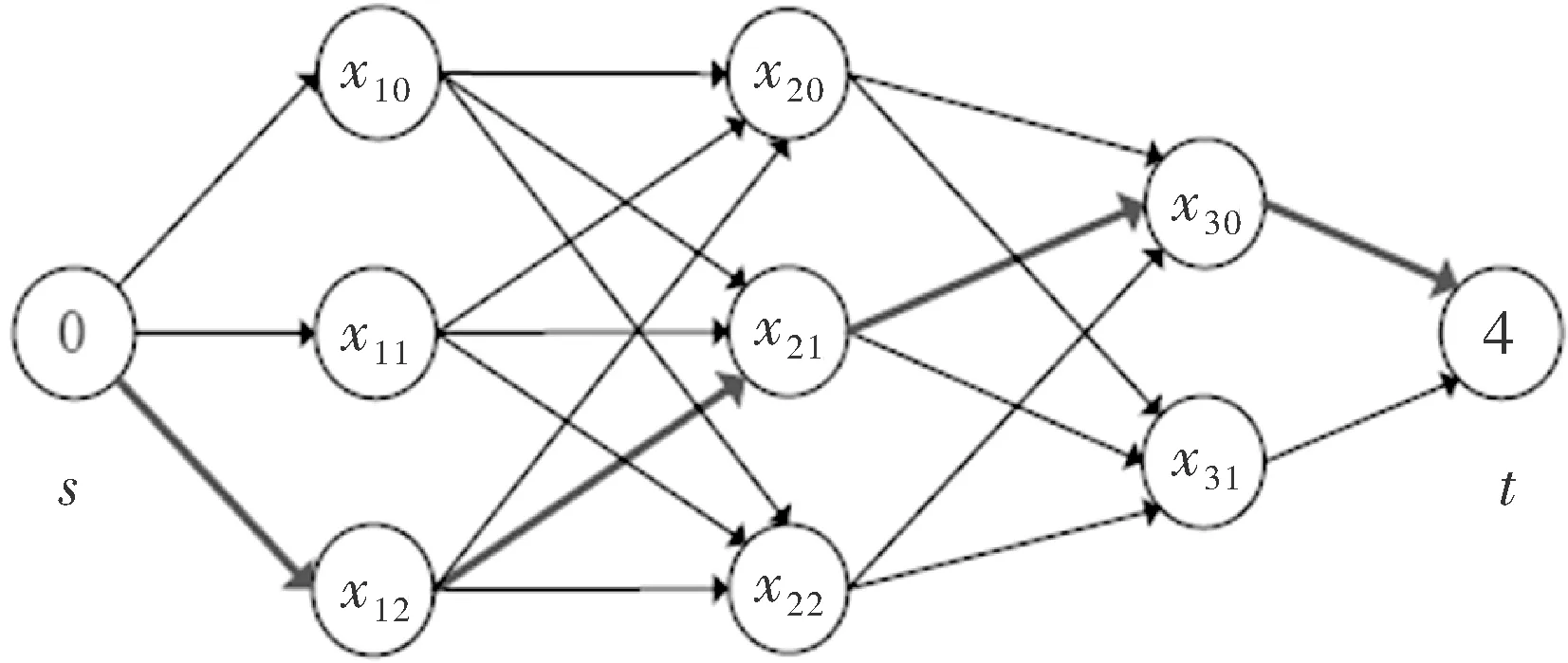
图2 多级图举例

2.2 基于动态规划算法的目标函数

根据研究问题的性质，本文提出了一个两步混合智能算法来优化被任意选择的解决方案。其基本思想是：在第一步，使用模拟退火算法求出待处理的序列。在建立最优轮廓序列时，将问题转化为动态规划算法求解的多段图问题。最终通过多次迭代得到最优解。

因此，图2中在计算起点s到终点t的目标函数时，算法可分为两步。第一步是确定从第k-1级所有的点到终点t的目标函数值。第二步是确定从第k-2级所有的点到终点t的目标函数值。第二步需要使用第一步中获得的信息。算法重复迭代多次，直到得到从起点s到终点t的最小目标函数值。

在执行过程中，该算法使用结构体PInfo来储存多级图中某个节点的数据。其数据结构在程序中的定义是：

struct PInfo

{

double x,y;

double m_cost;

int m_index;

}

vector< PInfo > m_vp;

每一次迭代过程中，节点的数据就会变化。而在每轮开始迭代时，结构体PInfo的数据中，m_cost和m_index这两个变量会初始化为最大和0。因此，文中的动态规划函数被定义为

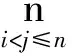
(1)

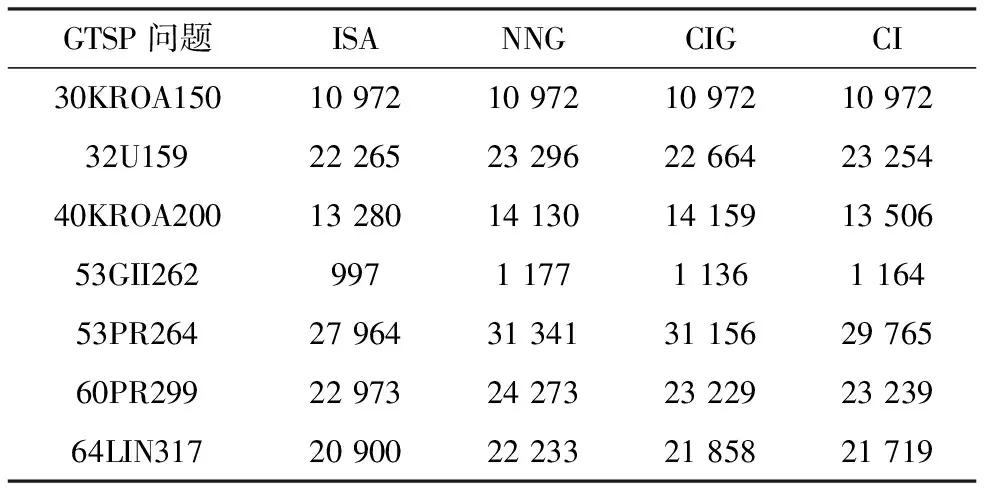
m_vp[i].m_index=j,i

(2)

其中，i，j是点群中的节点数字；cij表示节点i,j的距离。这个函数的目的就是令cij+m_vp[j].m_cos变得最小。

从图2中可看出，排列顺序不同的点就表示了不同的方案，而这些方案从起点x到终点t的最小距离又均是不同的。所以，衡量这些方案的目标函数的定义为

f(x)=1/(m_vp[0].m_cost+1)

(3)

其中，m_vp[0]是被评估的方案的起点。

2.3 改进算法具体步骤

模拟退火算法中包含3个函数和两个指标：生成新的解决方案的函数、衡量每个解决方案的函数、每轮温度变化的函数，以及终止算法内部循环和算法外部循环的两个指标。算法的精心设计使得模拟退火算法表现良好。模拟退火算法可以脱离局部极大值或者极小值，最终找到全局最优解，主要是因该算法根据不同的概率来接受新方案。然而，算法一开始运行就达到全局收敛条件是极少的。依照某一概率来接收新产生的解决方案[13-16]，这种做法令原来的方案可以比在搜索时的中间方案差。实际中，由此运行的算法通常可接近最优解，但搜索效率比较差。因此，为了提高搜索效率，保留最佳方案，本文改进了传统的模拟退火算法，其具体步骤如下：

步骤1 给定初始温度T0，随机生成初始方案x，令best=x，确定没有更好方案产生之后的最大循环次数DIMINISHTNUM，早期终止条件AIM，马尔可夫链长L，aim=0，num=0，i=0；

步骤2i=i+1，若i≥L，转到步骤10；

步骤3 调用邻域搜索算法来生成一个新的方案x′；

步骤4 计算目标函数差ΔE，若ΔE<0，则x=x′，num=0，aim=0，转到步骤7；

步骤5 若exp(-ΔE/Tk)>RandFloat()，则x=x′，num=num+1，转到步骤7；

步骤6 num=num+1，转到步骤7；

步骤7 若aim=AIM，则结束算法运行，转到步骤10；

步骤8 若num>DIMINISHTNUM，则aim=aim+1，num=0；

步骤9 若f(best)≤f(x)，则best=x，转到步骤2，f是目标函数；

步骤10 输出最终方案，结束整个算法。

其中，Tk是第k轮的温度，其满足这一温度下降公式

(4)

当迭代的次数为k，等于温度下降的总次数时，终止算法。

3 实验仿真和分析

为进一步对提出算法进行性能分析和比较研究，文中用C++语言来编程求解GTSP。为比较改进模拟退火算法与其他3种算法求解GTSP问题的有效性，本文做了大量改进算法和其他算法的实验。这里所有的实验测试数据选取于标准GTSP问题库[16]，共选取了7组测试的数据，针对这7个问题，算法运行了20次(ISA表示本文改进后的算法)。表1详细地列出了上面所说的实验的结果，从结果中可以看出，对于每个图来说，图中点的个数较小时，各种算法之间的运行时间差别很小，但当图中点的个数增加，改进模拟退火算法的表现就优于其他算法，且该算法具有更好的全局性能。

表1 改进算法和其他算法的运行时间比较

动态规划算法是一种没有局部优化的确定性算法，该算法所获得的路径就是最优路径，切无需要考虑参数这一因素。其中，该算法的时间复杂度为Θ(n+m)，其空间复杂度为Θ(n)，而n是算法处理的封闭轮廓的数目。该算法的时间与空间复杂度均能完全满足总体的性能要求。

4 结束语

本文提出了一种改进的模拟退火算法来求解GTSP问题。首先，根据GTSP问题的性质，其可转化为多段映射问题，而多段映射问题可以通过动态规划算法来解决。通过测试标准的GTSP问题的数据，测试结果表明：与传统的模拟退火算法相比，改进后的算法可大幅缩短运行时间，并更容易得到最优解。尤其是在处理规模较小的问题时，算法的效率得到了显著改善。此外，算法的参数也会影响算法的执行效率，合适的参数使得算法能够发挥出更好的性能。但对于大规模问题，改进算法的效率仍有待进一步提高。

[1] 鲜敏,郑翔.模拟退火算法优化聚类头节点的MANET服务质量改进[J].计算机应用与软件,2015(4):326-329.

[2] 宋燕子.基于模拟退火算法的启发式算法在VRP中的应用[D].武汉:华中师范大学,2013.

[3] 熊慧,胡小伟,刘近贞.基于混合粒子群和模拟退火算法的聚焦性优化[J].航天医学与医学工程,2016,29(1):34-38.

[4] 裴小兵,贾定芳.基于模拟退火算法的城市物流多目标配送车辆路径优化研究[J].数学的实践与认知,2016(2):105-113.

[5] 屈国强.改进模拟退火算法求解煤场配煤优化问题[J].物流技术, 2016(6):90-93.

[6] 任乃飞,于璐.基于混合遗传算法的协同制造系统调度研究[J].电子科技,2016,29(6):29-33.

[7] 潘绍林,张显云,范旭亮,等.模拟退火算法的灰色模型钟差预报[J].测绘科学, 2016,41(3):23-27.

[8] 吴再新,高尚策,齐洁.求解动态车间调度问题的改进微粒群算法[J].电子设计工程,2016,22(1):26-30.

[9] 张思建,方彦军,贺瑶,等.基于模拟退火算法的AVS/RS多批货箱入库货位优化[J].武汉大学学报:工学版,2016,49(2):315-320.

[10] 刘宝友,王涛,马延龙.基于模拟退火算法的中超赛程编排优化研究[J].河北科技大学学报,2016,37(5):497-502.

[11] 周兰伟,陈国平,孙东阳,等.基于模拟退火算法的旋转梁压电分流电路优化[J]. 振动、测试与诊断,2016,36(2):315-320.

[12] 杨放青,黄胜,王超,等.应用多目标模拟退火算法的舰船方案优化研究[J].中国造船,2014(4):122-131.

[13] 孟凡超,初佃辉,李克秋,等.基于混合遗传模拟退火算法的SaaS构件优化放置[J].软件学报,2016,27(4):916-932.

[14] 杨卫波,王万良,张景玲,等.基于遗传模拟退火算法的矩形件优化排样[J].计算机工程与应用,2016,52(7):259-263.

[15] 李仲欣,韦灼彬,沈锦林.高效的自适应小生境遗传-模拟退火混合算法[J].计算机工程与设计,2016,37(4):1004-1010.

[16] Reinelt G,Tspli B. A traveling salesman problem library[J].ORSA Journal on Computing,1991,3(4):376-384.

Improved Simulated Annealing Algorithm for Traveling Salesman Path Planning Problem

ZHOU Jun1，JIA Kunlin2

(1.Academic Affairs Department, Huizhou Engineering Technology School, Huizhou 516001, China;2. Training Center, Business and Tourism Advanced Vocational Technology School, Huizhou 516000, China)

The traveling salesman path planning problem (GTSP) is a typical NP complete problem. In this paper, an improved simulated annealing algorithm is proposed to solve the GTSP problem. The improved algorithm overcomes some disadvantages of the traditional simulated annealing algorithm. Specifically, the GTSP problem can be transformed into a multi-segment map problem, which can be solved by the dynamic programming algorithm at a greatly shortened running time of the whole algorithm. A large number of experimental results show that the improved simulated annealing algorithm can converge in a shorter time and get better solution than the traditional simulated annealing algorithm.

simulated annealing algorithm; dynamic programming algorithm; traveling salesman path planning problem; objective function

2016- 12- 20

周君(1979-)，男，讲师。研究方向：计算机编程。

10.16180/j.cnki.issn1007-7820.2017.07.017

TP301.6

A

1007-7820(2017)07-062-04