基于超声波的多元线性回归测量模型研究

张婧婧，李勇伟

(1.新疆农业大学 计算机与信息工程学院，新疆 乌鲁木齐 830052;2.新疆农业大学 机械交通学院，新疆 乌鲁木齐 830052)



基于超声波的多元线性回归测量模型研究

张婧婧1，李勇伟2

(1.新疆农业大学 计算机与信息工程学院，新疆 乌鲁木齐 830052;2.新疆农业大学 机械交通学院，新疆 乌鲁木齐 830052)

以非规则物体尺寸测量为研究目标，以超声波测距和线性回归理论为研究基础，进行了基于超声波的多元线性回归模型分析。系统硬件设计以STM32为主控平台，利用超声波模块采集5路测距值作为线性方程的自变量；再通过非规则物体周长的人工测量，得到方程的因变量，展开模型的多元线性回归分析。通过回归方程的建立，定量展示了基于机器学习的测量方案具备显著优势，为同类测量系统提供了一种成本的设计参考。

超声波测距；机器学习；多元线性回归；STM32处理器

1 测量模型及测距原理

1.1 建立特定测量模型

如图1(a)所示，实验中选取了20个同心的非规则椭圆柱面为测量模型，用于描述某类非规则物体或工件的尺寸设计规律，亦可将其视为动物生长过程的体尺变化规律，建立类似的线性回归模型[9-10]。在模型中选取A、B、C、D、E共5个固定测试点，分别布置相应的超声波测距模块，用于返回各曲线切面与固定点的距离，构成线性回归方程的自变量；而非规则椭圆柱的周长则通过人工测量，构成线性回归方程的因变量，利用机器学习建立回归方程。

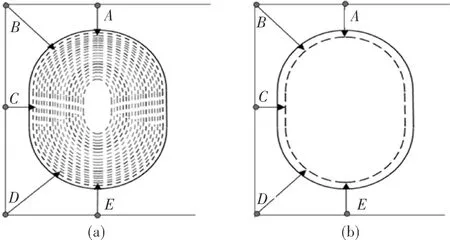
图1 非规则物体测量模型的切面图

图1(a)选取了第21个任意同心椭圆柱曲面(如虚线所示)。通过固定点的测距提取自变量，代入图1(b)建立的方程，验证模型的线性回归特性，进一步完成任意周长的机器计算与数据的分析对比。

1.2 超声波测距原理

超声波属于一种声波，使用其测距时，首先需要确定声速，其次需要获得超声波往返所需的时间，即可得到距离[11]。其计算公式为

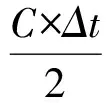
(1)

其中，S为被测距离；C是超声波在空气中的传播速度；Δt是超声脉冲发射与接收其回波的时间差；t1为超声回波接收时刻；t0为超声脉冲发射时刻。由于声速C与空气温度有关，测距时温度变化微弱且测量精度要求不高，因此计算过程中取值均为340 m/s。

2 测距系统的建立

2.1 测距系统的设计框架

（3）城乡规划教学方式与内容面临的调整。现有的课程讲授“重理论轻分析”，无法应对大数据时代带来的变化与挑战。现有课程讲授以理论概念及运用为主，对信息数据的缺乏分析，对如何在调研数据基础上推导出的理论缺乏相应讲解，对数据分类、处理以及分析的技术手段与方法缺乏相关课程培训，导致学生在面对新问题时束手无策。

如图2所示，系统选用STM32作为主控芯片[12-13]。根据测距要求，首先利用主控器STM32中通用定时器的PWM输入模式捕获边沿时间，再通过边沿触发的外部中断计算超声波脉冲的高电平时间，代入式(1)即可得到测试点与切面的间距，并依据相同的测距原理设计状态机，依次进入五路超声波测距状态，接收测试数据后封装并通过串口向外发送，即可获取线性回归模型中的自变量(x1,x2,x3,x4,x5)。

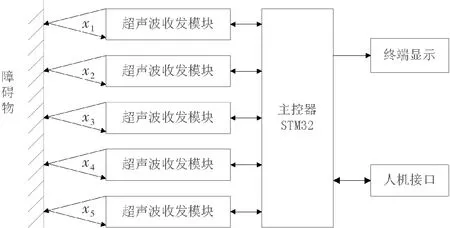
图2 测距系统的设计框图

2.2 系统硬件工作原理

系统选用的CPU为SMT32VET6[14]，外设资源包括全速USB Device，SDIO，SPI，I2C，I2S，FSMC，定时器，USART，ADC，DAC，CAN 等接口。其MCU为STM32F103高容量芯片，内部有8路通用的16位定时器，满足实验中测距模块的各项要求，其测距原理如图3所示。

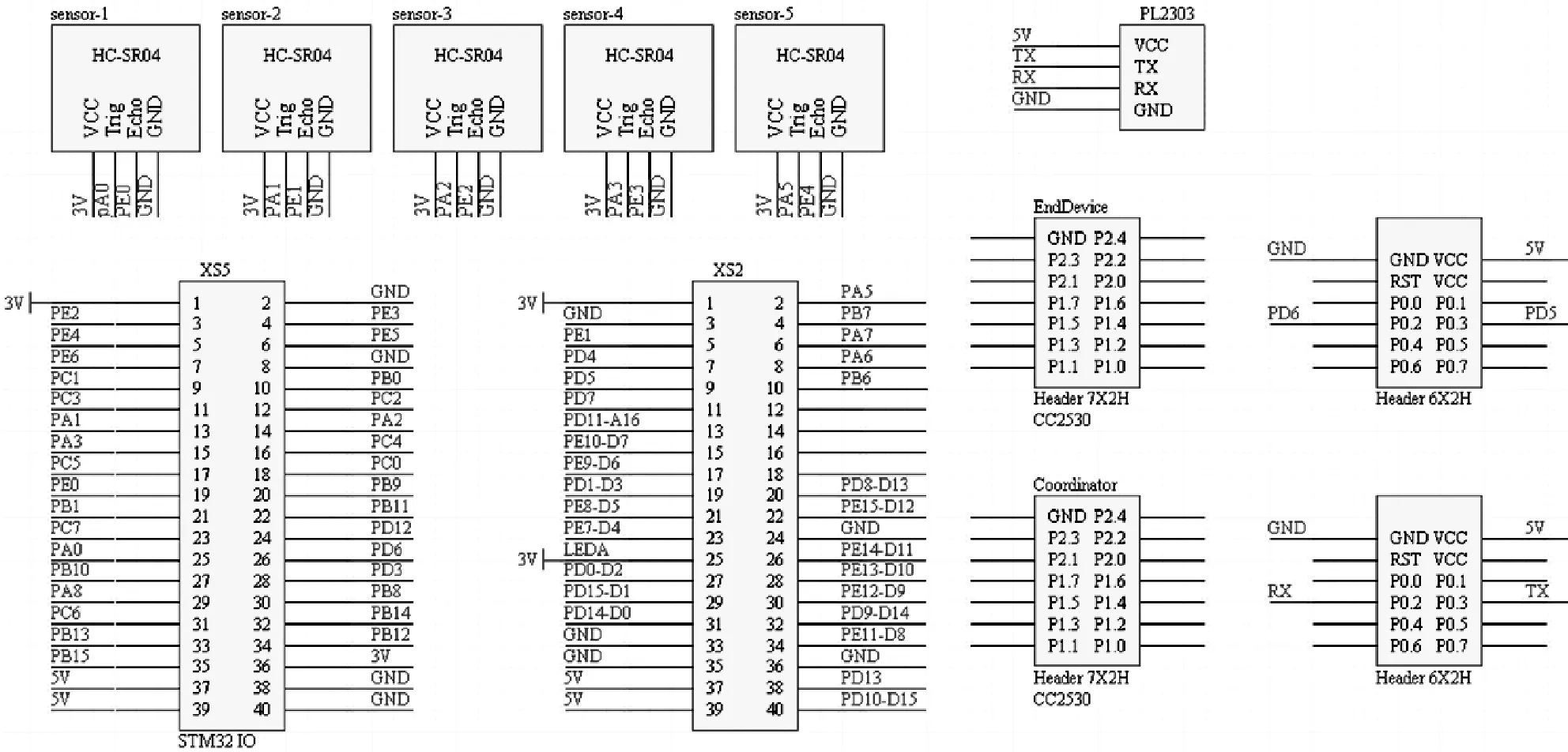
图3 超声波测距系统的设计原理图

如图3所示，系统设计基于STM32的主控平台，首先依次采集5路超声波的测距值，再将数据通过ZigBee模块子节点(EndDevice)传至协调器(Coordinator)，然后利用USB转串口模块发送数据至上位机，最终完成系统的数据采集、控制、发送及终端显示等部分的硬件设计。

2.3 软件设计流程

如图4所示，通过状态机的设计，系统依次进入接收5路超声波测距的状态，并将数据封装、传送至PC机，然后通过数据解析完成各路距离值的最终显示，设计中采用的开发环境为STM32CubeMX、Keil MDK uVsion5。

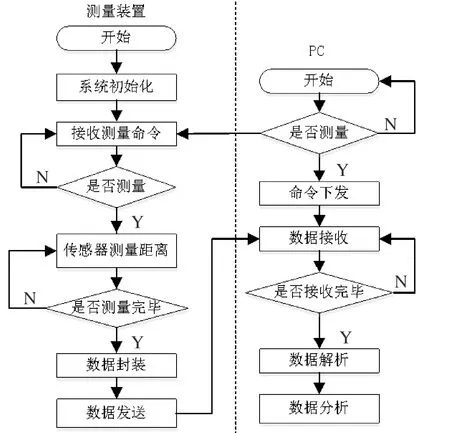
图4 测距系统的主程序流程设计

3 多元线性回归分析

基于机器学习和超声波测距理论，在采集如图1所示测量模型的数据后，选择了Matlab的Regress方法完成此模型多元线性回归分析。

3.1 多元线性回归模型

y=b0+b1x1+…+bpxp+e

(2)

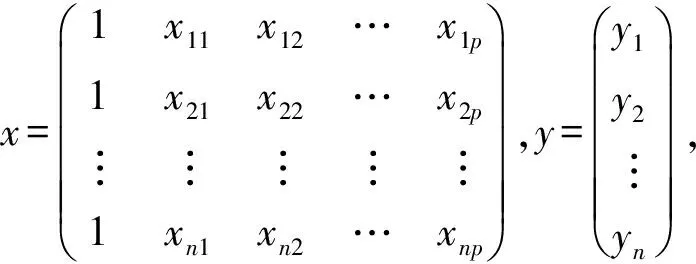
如式(2)所示，模型中自变量x1,x2,x3,x4,x5取自超声波模块获得的5个测试点与切面的间距，应变量y则由人工测量的各个相应切面的周长数据构成。

3.2 模型的测试数据

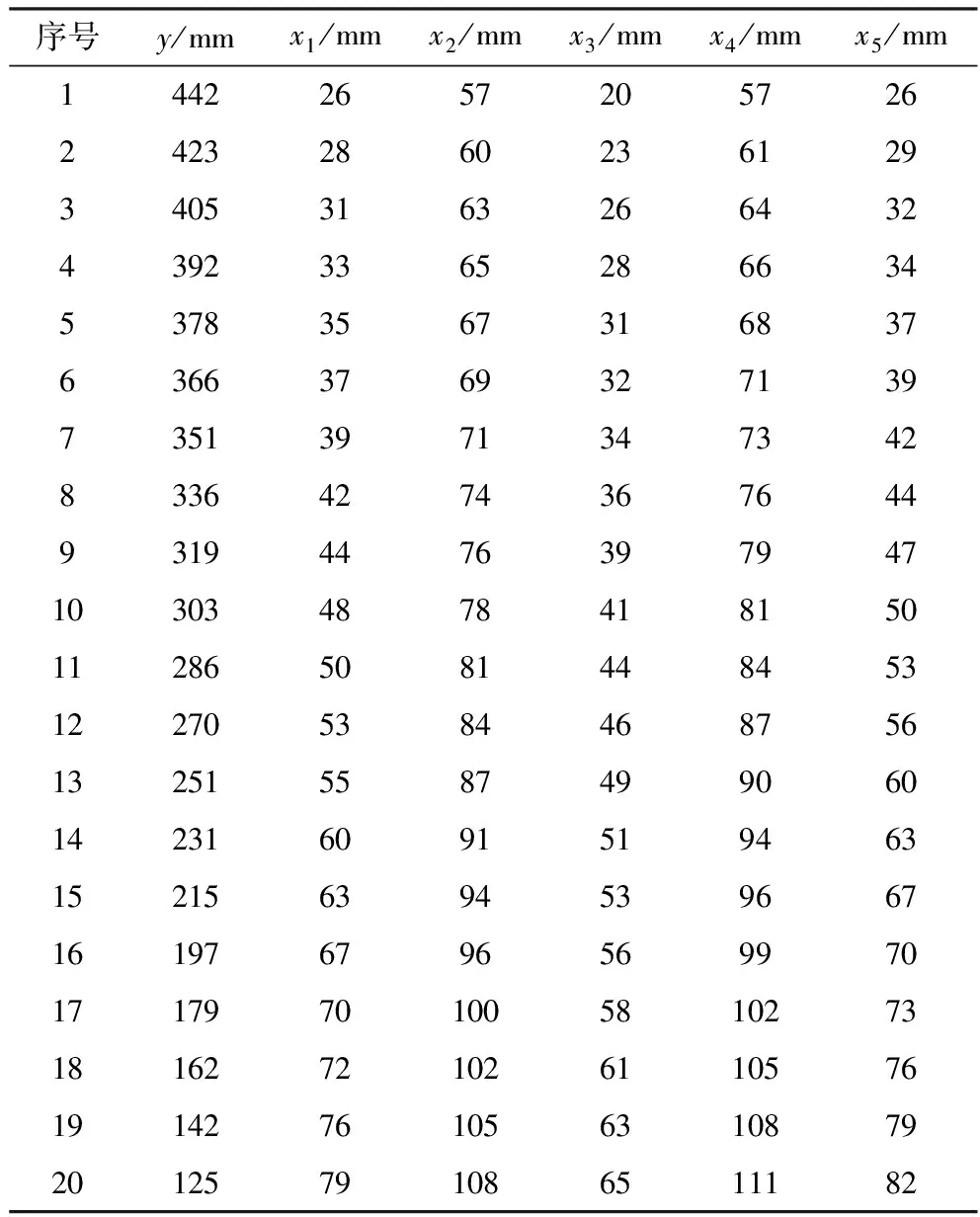
表1 多元线性回归模型的数据列表

根据测距系统的实验结果，所得数据如表1所示。利用20个同心的非规则椭圆柱面，测距时依次获得20组固定测试间距xn和相应圆柱面周长yn，n=1,2,3…20，据此进行如下的多元线性拟合。

4 残差分析与线性拟合

4.1 残差分析

为检验超声波测距效果是否理想，首先根据残差的置信区间进行残差分析。

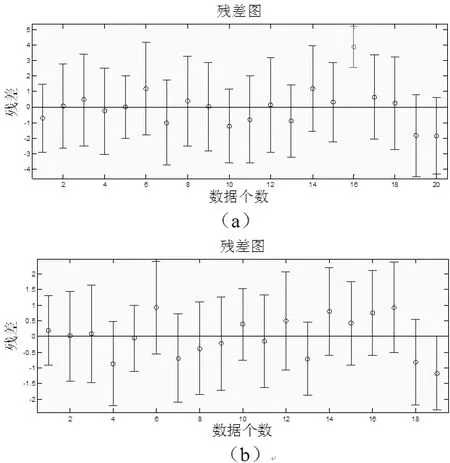
图5 多元线性方程的残差图

如图5(a)所示，除第16个数据外，其余数据的残差距零点均较近，且残差的置信区间均包含零点。剔除第16个异常点的数据如图5(b)所示，回归模型能较好的反映原始数据的变化规律。

4.2 多元线性拟合

据上述残差分析，实验中将异常点除去后的19个原始数据代入Matlab中Regress方法进行线性拟合，获取回归系数b，得到线性回归方程

y=640.790 2-1.613 4×x1-0.712 1×x2-
1.430 6×x3-2.355 4×x4-1.336 8×x5

(3)

其中，检验回归模型的统计量r2=0.999 9；F=596 10；P=7.371 0-28。由P可知，式(3)的回归模型成立，其拟合曲线如图6所示。

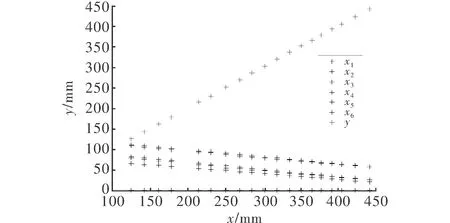
图6 多元线性方程的拟合曲线

将图1(b)第21组数据代入线性回归方程式(3)中，即x1=30 mm；x2=63 mm;x3=26 mm;x4=64 mm;x5=34 mm;y(计算值)=403.9 mm;y(实验值)=402.2 mm；误差为0.42%

5 结束语

(1)对某一超声波测距模块而言，在理想系统时间分辨率下，测量的精度可达1 mm，但就规则物体的周长指标而言，其测量误差往往会叠加，因此很难有效提高其测量的准确性。相比之下，基于机器学习的尺寸测量方案更具精度优势，且适用性更为广泛；(2)设计中采用的超声波仍沿用其一般测距原理，但无需进行温度补偿和误差修正。因为通过机器学习，已将测量值纳入多元线性回归方程的自变量范畴，弱化其精度需求的同时将其测距功能和效果大幅提高；(3)多元线性回归方程中，测试数据维数越多，预测值将越准确。而基于嵌入式或单片机的控制系统中，超声波测距节点的个数受到测量周期和反射距离的限制，需要考虑降低发射信号对回响信号的影响，因此在不同测量方案中自变量维数的选取还需参考主控器的类型和实测距离的变化。

[1] 刘升平,王剑,葛红.超声波测距系统的开发与研究[J].计算机工程与应用,2009,45(25):78-81.

[2] 莫德举,刘艳艳.超声波液位测量方法的研究[J].仪表技术与分析检测,2007(1):45-48.

[3] 瞿金辉,周蓉生.超声波测距系统的设计[J].中国仪器仪表,2007(8):43-45.

[4] 邹伟,李丽,王秀,等.超声波传感器测距实验平台设计与实验[J].传感器与微系统,2011,30(10):89-92.

[5] 李卞俊,杨录,张艳花.双门选超声波收发模拟电路的设计[J].电子科技,2016,29(3):151-153.

[6] 韩军,常瑞丽.智能移动机器人超声波测距定位系统的研究[J].机械设计与制造,2010(1):164-166.

[7] 沙爱军. 基于单片机的超声波测距系统的研究与设计[J].电子科技,2009,22(11):57-61.

[8] 祝敏.超声波测距误差分析及修正方法[J].计量与测试技术,2009,36(2):21-22.

[9] 王惠文,孟洁.多元线性回归的预测建模方法[J].北京航空航天大学学报,2007,33(4):500-504.

[10] 信玉翠,王伟伟,徐安杨,等.线性回归中自相关问题在建模中的求解与研究[J].数学学习与研究,2016(13):117-120.

[11] 卜英勇,王纪婵,赵海鸣,等.基于单片机的高精度超声波测距系统[J].仪表技术与传感器,2007(3):66-68.

[12] 李成,李立伟,张洪伟.基于STM32单片机的数据记录装置设计[J].工业控制计算机,2013,26(1):91-92.

[13] 徐宏宇,沈煌飞.基于STM32 的多点温度检测系统设计[J].电子科技,2016,29(5):158-161.

[14] 夏继强,郑昆,郑健峰,等.基于STM32的收发一体式超声波测距系统[J].仪表技术与传感器,2014(8):43-45.

[15] 虞晓胤,杨小虎.功能性回归测试工具分析[J].计算机应用与软件,2007,24(5):175-177.

Research on the Model of Multiple Linear Regression Based on Ultrasonic

ZHANG Jingjing1，LI Yongwei2

(1.School of Computer and Information Engineering, Xinjiang Agricultural University, Urumqi 830052, China;2. School of Mechanical Transportation, Xinjiang Agricultural University, Urumqi 830052, China)

In this paper, we analyze the multiple linear regression model based on ultrasonic for irregular object size measurement. The hardware design of the system is based on the STM32 control platform, and the independent variable of linear equation is provided by using the ultrasonic module to collect the range value of 5 channels; then through artificial measurement of irregular objects of the perimeter, we get the equation dependent variables, and then the multiple linear regression analysis of the model is carried out. The establishment of regression equation offers the measurement scheme based on machine learning significant advantage, which provides the design reference for the similar measurement system.

ultrasonic distance measurement; machine learning; multiple linear regression; STM32 processor

2016- 09- 02

新疆农业大学校前期基金(XJAU201516)

张婧婧(1981-)，女，硕士，高级实验师。研究方向：嵌入式技术与应用。李勇伟(1973-)，男，硕士，讲师。研究方向：传感器技术与应用。

10.16180/j.cnki.issn1007-7820.2017.07.016

TP181;TM343; G712

A

1007-7820(2017)07-058-04