边权重的混合攻击策略
章 鹏,韩 华,谢先招,王海军
(1.武汉理工大学 理学院,湖北 武汉 430070;2.华中科技大学 管理学院,湖北 武汉 430074)
边权重的混合攻击策略
章 鹏1,韩 华1,谢先招1,王海军2
(1.武汉理工大学 理学院,湖北 武汉 430070;2.华中科技大学 管理学院,湖北 武汉 430074)
鉴于当前网络攻击策略多样化和复杂化的现状,提出了以边权重作为度量复杂网络中边重要性的指标,并与传统的边介数度量指标进行了对比分析。通过4种类型的仿真网络,论证了边权重的合理性和有效性,并在边攻击策略的基础上提出了一种混合攻击策略。将新的攻击策略与传统的点攻击策略和边攻击策略进行对比分析,仿真结果表明:所提出的混合攻击策略对网络造成的破坏程度明显大于传统的点、边攻击策略。当网络崩溃时,混合攻击策略的攻击次数几乎为点攻击策略的一半。
复杂网络;边权重;边介数;鲁棒性;混合攻击
0 引言
将复杂网络理论应用于不同类型的网络中,分析不同攻击策略下各类网络的鲁棒性,对不同类型网络的攻防对抗具有一定的理论价值和现实意义。目前,大多数复杂网络研究者主要针对网络中的节点以及连边进行了比较深入的研究。文献[1]主要运用复杂理论中的相关度量指标识别出海运航线网络中的关键港口,提出一种识别网络中关键节点的方法。文献[2]综合考虑边介数和边的两个端点对边的支撑作用,提出了新的关键边评估模型,但其时间复杂度较高。文献[3]通过增加连边来提高网络的鲁棒性。文献[4]研究了向网络中加边后网络的容量变化情况。文献[5]提出了两种提高网络抗毁性的方法,一种方法是向网络中加边后达到增强网络鲁棒性的目的;另一种方法是隐藏网络中的重要边,避免其被攻击。文献[6]提出了两种边修改策略以提高网络的鲁棒性,一种是重连网络中的部分连边;另一种是向网络中添加新的连边。文献[3-6]均通过对边进行相应的处理来提高网络的鲁棒性,但并没有采用与边有关的鲁棒性衡量指标,所以网络的鲁棒性变化并不能得到很好的体现。文献[7]提出一种网络优化策略以提高网络的鲁棒性,并与传统的优化策略进行对比分析,论证了所提出的策略的有效性。文献[8]采用3种攻击策略,以及去点和去边两种攻击方式,研究了作战体系网络的抗毁性,但忽略了同时去点和去边的攻击方式。
基于上述研究,本文提出了一种时间复杂度较低的边重要性度量方法,并与传统的边介数[9]进行对比研究。论证了边权重作为边重要性度量指标的合理性和有效性,提出了基于边权重的混合攻击策略,同时与传统的点攻击策略和边攻击策略进行对比分析,对于研究如何提高网络的鲁棒性具有重要意义。
1 基于边权重的边攻击策略
1.1 边权重
文献[10]指出,复杂网络中边的介数与该边的两个端节点的度的乘积是正相关的。即边权重wij可以表示为:
wij=wji=kikj,
(1)
其中:ki和kj分别为节点i和节点j的度。本文以wij作为网络中边的重要性度量指标,其时间复杂度为O(N2)。
传统的边介数有较高的时间复杂度O(N3),并且在现实网络中获取边的全局信息的难度非常大。基于此,本文根据边的局部信息,以式(1)中的wij作为边的重要性度量指标,其时间复杂度比边介数低。为了进一步论证以边权重作为边重要性度量指标具有合理性,选取不同的网络研究对象与边介数进行对比分析。
1.2 边连通率
衡量网络受到攻击后的鲁棒性指标有连通度、黏聚度、坚韧度、完整度、离散度和网络效率等[11],然而网络的鲁棒性衡量指标却常常因为研究对象的不同而不尽相同。文献[12]在无标度网络的鲁棒性研究中,采用点连通率S(v)作为网络鲁棒性的衡量指标。为了更好地刻画网络中连边的变化情况,提出了新的网络鲁棒性衡量指标S(e):
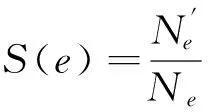
(2)
1.3 边攻击策略对比仿真分析
本文选取4种类型的仿真网络作为研究对象,包括Barabasi-Albert(BA)无标度网络、Erdos-Renyi(ER)随机网络、小世界网络和规则网络[13-16]。本节所构建的网络规模N=500。
为了说明边权重相对于边介数作为衡量边重要性指标的合理性和有效性,通过删除对应比例的连边,观察删除连边后的网络拓扑结构变化情况,以此判断边的重要性。分别采用基于边介数的边攻击和基于边权重的边攻击进行对比,并以点连通率S(v)和边连通率S(e)作为网络鲁棒性的衡量指标。不同边攻击方式下的点连通率变化如图1所示。
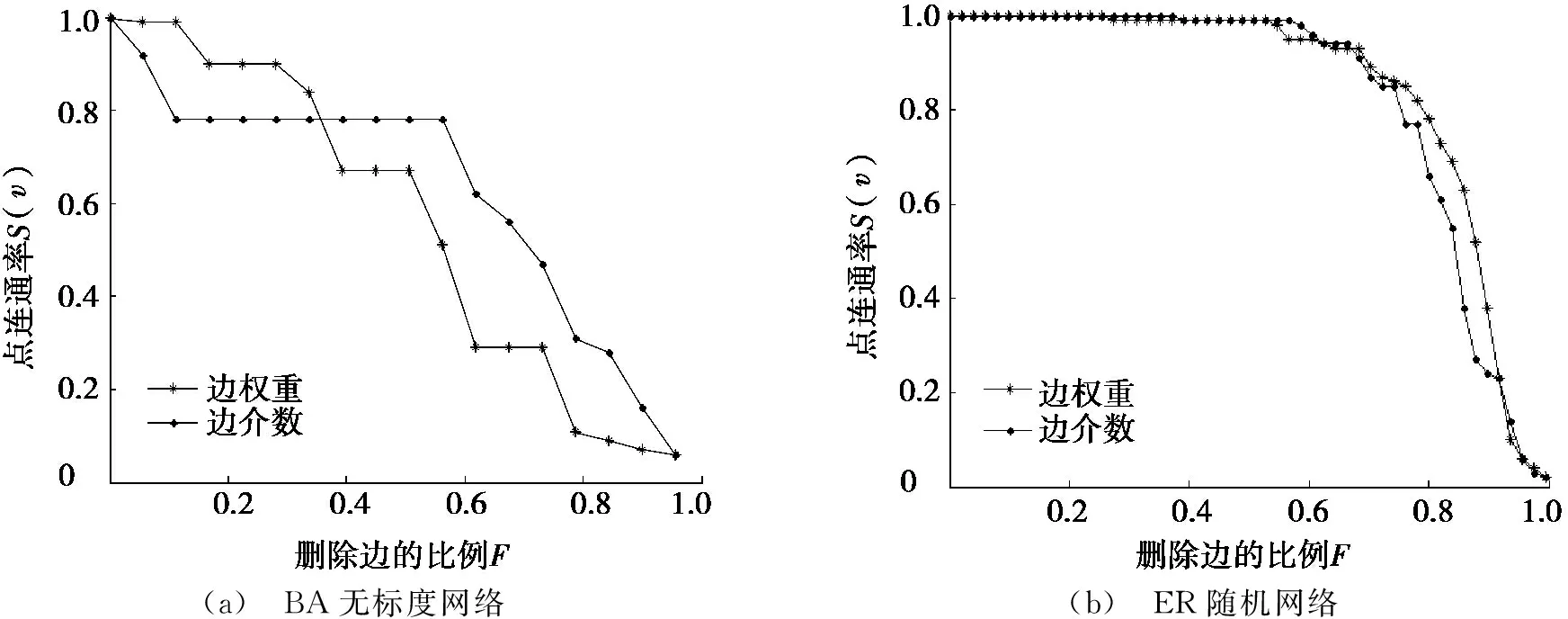
(a) BA无标度网络(b) ER随机网络
图1 不同边攻击方式下的点连通率变化
由图1a可以看出:在BA无标度网络中,当删除边的比例F<0.38时,基于边介数的边攻击方式优于基于边权重的边攻击方式;而当删除边的比例F>0.38时,随着删除边的比例F的增加,基于边权重的边攻击方式明显优于基于边介数的边攻击方式。这是由BA无标度网络的拓扑结构特性所决定的,其少数的hub节点(度较大的节点)对应着极少数的“关键边”,在删除边的比例F<0.08之前,随着“关键边”的断开,网络鲁棒性急剧下降,此时网络拓扑结构发生明显变化;当删除边的比例在F=0.08与F=0.54之间时,基于边介数的边攻击方式没有使网络的鲁棒性发生变化。而当BA无标度网络的拓扑结构发生变化后,基于边权重下的边攻击方式却变得更为有效,当删除边的比例F>0.38时,删除同样比例的边,基于边权重的边攻击方式给网络造成的破坏程度要大于基于边介数的边攻击方式。由图1b可以看出:在ER随机网络中,两种边攻击方式对网络造成的破坏程度并无明显差异。这是由随机网络的构建原理造成的,随机网络在随机生成的过程中,网络中所有边的重要性并无明显差异,当删除同样比例的连边时,网络的鲁棒性变化情况基本一致。在小世界网络中也可以得出类似随机网络中的结论,然而在规则网络中,基于边权重的边攻击方式明显优于基于边介数的边攻击方式。
不同边攻击方式下的边连通率变化如图2所示。由图2a可以看出:在BA无标度网络中,当删除边的比例F<0.13时,基于边介数的边攻击方式略优于基于边权重的边攻击方式;而当删除边的比例F>0.13时,基于边权重的边攻击方式却明显优于基于边介数的边攻击方式。此结论与图1a中的BA无标度网络呈现出来的鲁棒性变化并无明显差异,说明了以边连通率作为网络鲁棒性的衡量指标的合理性。由图2b可以看出:在ER随机网络中,两种边攻击方式给网络造成的破坏程度基本相同。在小世界网络中,两种边攻击方式对网络造成的破坏程度基本一致。在规则网络中两种边攻击方式也表现出了相似的鲁棒性变化规律,随着删除边的比例的增加,两种边攻击方式并没有使最大连通子图中边的数量发生太大的变化,导致两种边攻击方式下的网络鲁棒性变化差异并不明显。
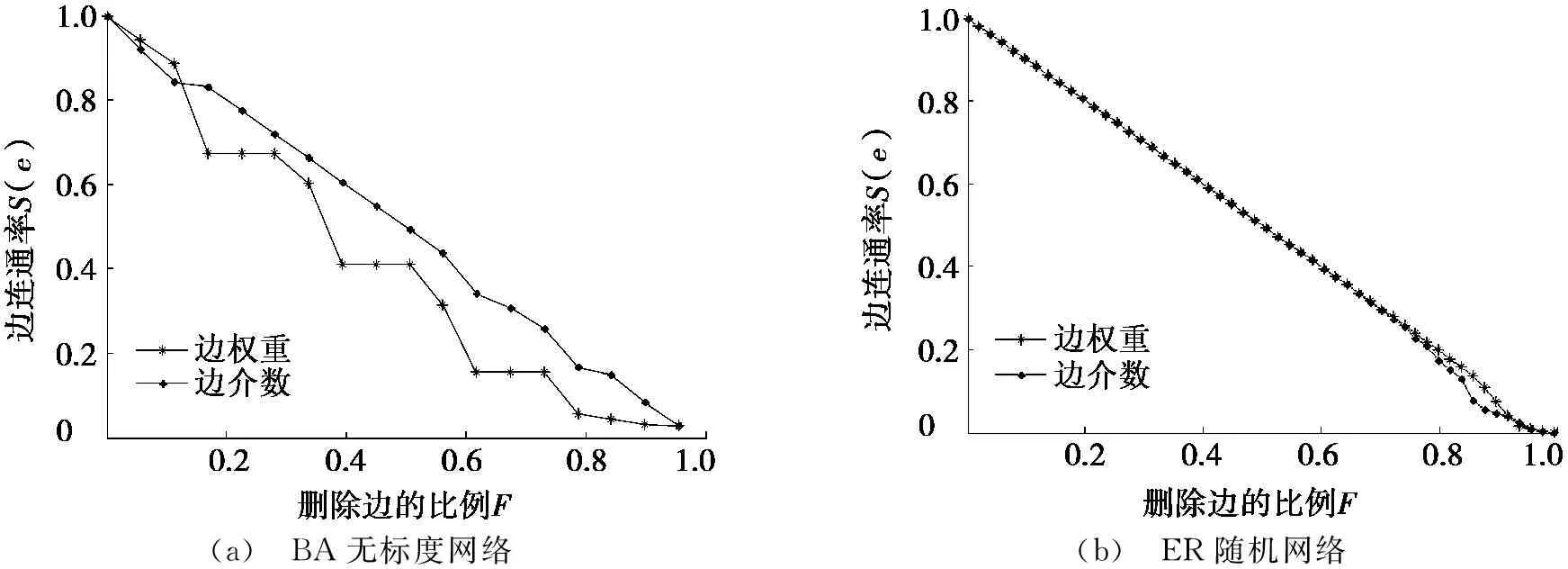
(a) BA无标度网络(b) ER随机网络
图2 不同边攻击方式下的边连通率变化
上述研究表明:边权重作为边重要性度量指标具有合理性及有效性,同时降低了度量边重要性的时间复杂度,并克服了在现实网络中获取边的全局信息所遇到的困难。
2 混合攻击策略
网络的攻击方式一般可以分为去点攻击和去边攻击,点攻击策略是根据节点度的大小顺序进行攻击;而边攻击策略就是根据边权重的大小顺序进行攻击。不同的攻击方式又可以分为随机攻击和蓄意攻击两种类型。
2.1 混合攻击算法
随着新的网络攻击方式的增多及攻击复杂性的提升,提出了一种混合攻击策略。首先,衡量边的重要性wij并将其按降序排列,攻击边重要性最高的连边emn,并对该连边的两个端节点m、n进行攻击,即对网络中的连边及两个端节点同时进行攻击。然后,将剩余网络中的连边再次进行度量并排序,重复上述攻击策略,随着攻击次数的增加,网络的鲁棒性也随之变化,直至网络的鲁棒性指标边连通率S(e)和点连通率S(v)变为0,攻击结束,将这种攻击策略称为混合攻击。为了与混合随机攻击加以区别,混合攻击也称为混合蓄意攻击。混合攻击示意图如图3所示。图3中:t为攻击次数。
图3a为初始网络,通过式(1)计算可知:边emn的边权重wmn最大。根据混合攻击的定义,将边emn及其两端节点m、n去掉,得到攻击1次后的网络拓扑结构,如图3b所示。根据图3,得到混合攻击算法的步骤如下:
步骤1:初始化网络,设置网络参数,根据网络构建机制得到网络G=(V,E)。
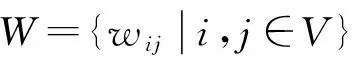
步骤4:采用混合攻击策略,将边权重最大的连边wmn及其两个端节点m、n去掉(当边权重的最大值相同且有多个时,则随机选择一条权重最大的边进行混合攻击)。
步骤5:计算最大连通子图中的连边数和节点数,根据式(2)算出边连通率S(e)和点连通率S(v)。
步骤6:判断网络的边连通率S(e)和点连通率S(v)是否为0,是则进入步骤7,否则返回步骤2。
步骤7:攻击结束。
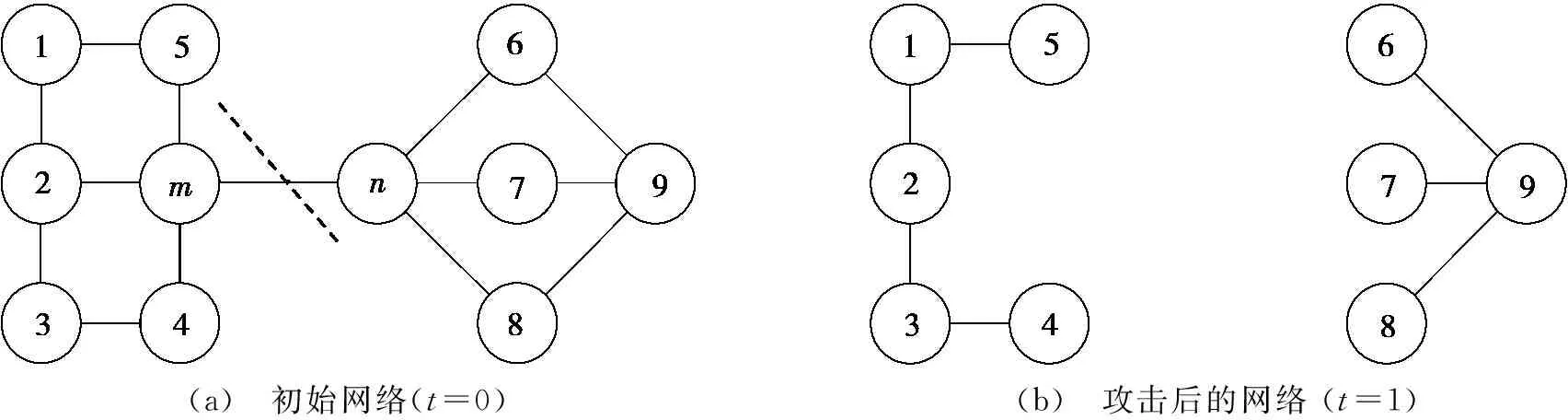
(a) 初始网络(t=0)(b) 攻击后的网络(t=1)
图3 混合攻击示意图
2.2 仿真分析
为了研究混合攻击策略给网络造成的损坏程度及摧毁性速率,本文主要选取了BA无标度网络、小世界网络和ER随机网络作为研究对象,分别对这3种网络进行混合攻击、点攻击和边攻击,然后对3种攻击策略进行对比分析,每种攻击策略分别对应随机攻击和蓄意攻击两种攻击类型。本文与文献[17]做同样假设,即当点连通率S(v)或边连通率S(e)小于5%时,网络崩溃。
BA无标度网络中,不同攻击策略下的边连通率和点连通率如图4所示。从图4中可以明显看出:选取点连通率S(v)和边连通率S(e)分别作为网络鲁棒性衡量指标,所呈现出的攻击效果基本一致,即混合攻击策略摧毁网络所攻击的次数最少,点攻击策略次之,而边攻击策略的攻击次数最多。由图4a可以看出:在BA无标度网络中,攻击次数t相同时,混合攻击策略对网络造成的摧毁程度明显优于点攻击策略和边攻击策略。在BA无标度网络中,混合攻击策略的随机攻击方式对网络的摧毁速率仅次于点攻击策略中的蓄意攻击方式,当网络崩溃时,混合随机攻击需要攻击的次数为30次,而点蓄意攻击也需要攻击29次。与图4a中的边连通率不同,图4b主要以点连通率作为BA无标度网络的鲁棒性衡量指标,由图4b得出的结论与图4a中的结论基本一致,即混合攻击策略下的网络鲁棒性最弱,边攻击策略下的网络鲁棒性最强。而在ER随机网络和小世界网络中,混合攻击策略的随机攻击方式对网络的摧毁速率要高于点攻击策略中的蓄意攻击方式,由此可以看出混合攻击策略给网络带来了毁灭性的攻击。
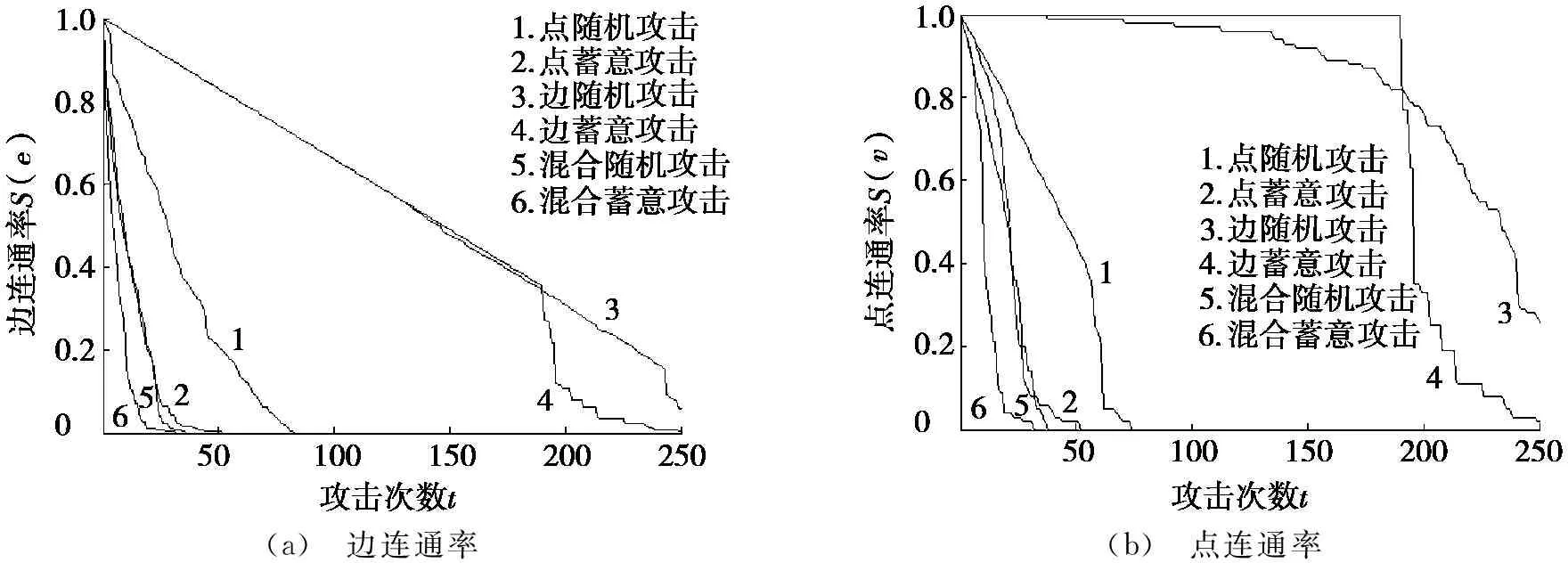
(a) 边连通率(b) 点连通率
图4 BA无标度网络中,不同攻击策略下的边连通率和点连通率
考虑到现实生活中大多数网络都具有无标度特性,选取3种规模的BA无标度网络,网络规模分别为N=100、N=200、N=300,并分别对其进行混合随机攻击和混合蓄意攻击。不同规模BA无标度网络的边连通率和点连通率如图5所示。由图5a可以看出:在相同规模的网络中,混合蓄意攻击使网络崩溃的攻击次数均明显小于混合随机攻击。当N=100时,混合蓄意攻击需要攻击17次可使网络崩溃,而混合随机攻击却需要攻击28次;当N=200时,混合蓄意攻击需要攻击29次可使网络崩溃,而混合随机攻击却需要攻击58次;当N=300时,混合蓄意攻击需要攻击43次可使网络崩溃,而混合随机攻击却需要攻击76次。在不同规模的网络中,选择同样的网络攻击方式,攻击网络至网络崩溃的次数随着网络规模增加而增加,即当N=100时,混合蓄意攻击需要攻击17次;而当N=200时,混合蓄意攻击需要攻击29次;当N=300时,混合蓄意攻击需要攻击43次。由图5b也可以得到与图5a中一致的结论,在此不作赘述。
上述研究表明:混合攻击策略中的混合蓄意攻击要明显优于混合随机攻击,同时,混合攻击策略在攻击不同规模的网络时,所呈现出的攻击效果基本一致。
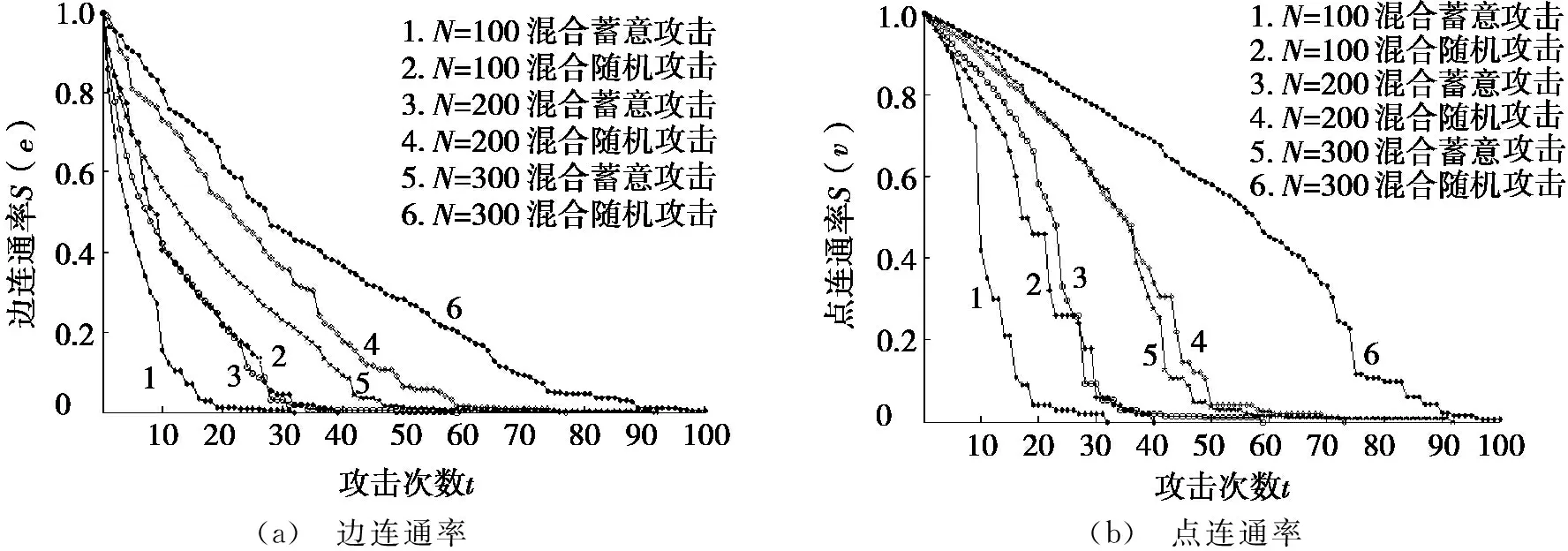
(a) 边连通率(b) 点连通率
图5 不同规模BA无标度网络的边连通率和点连通率
3 实证分析
将点攻击策略、边攻击策略和混合攻击策略用于实际网络,并观察其攻击效果。搜集道琼斯中国88指数(2011年11月1日—2013年5月31日)的数据,根据Pesrson相关系数法计算各股票之间的相关性得到相关系数矩阵C。采用最佳阈值法[18]对矩阵C处理得到相应的股票网络,并分别采用3种攻击策略对其进行随机攻击和蓄意攻击,得到股票网络在不同攻击策略下的边连通率和点连通率,结果如图6所示。
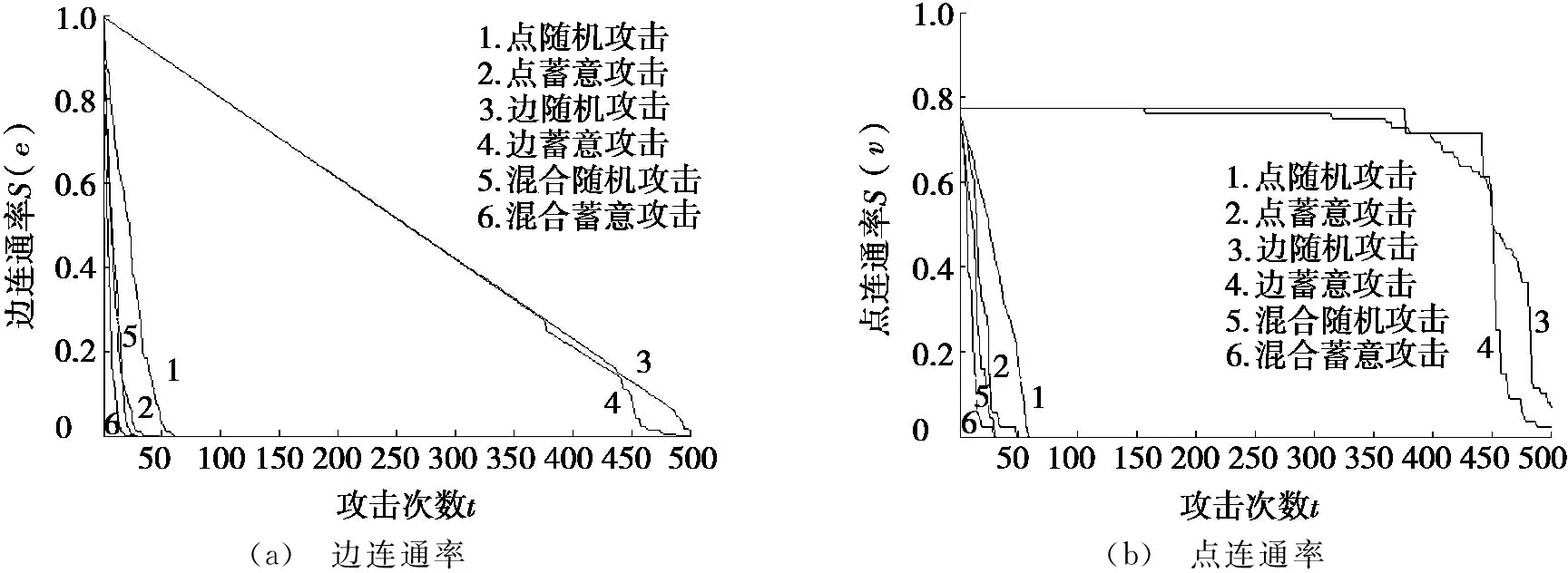
(a) 边连通率(b) 点连通率
图6 股票网络在不同攻击策略下的边连通率和点连通率
从图6中可以看出:在攻击次数t相同的情况下,混合攻击策略对股票网络造成的破坏程度大于点攻击策略,而点攻击策略给股票网络造成的破坏程度大于边攻击策略,即混合攻击策略给股票网络造成的破坏性最强。不难发现:混合攻击策略下的随机攻击优于点攻击策略下的蓄意攻击。从图6a中可以看出:混合随机攻击只需要攻击19次即可使股票网络崩溃,而点蓄意攻击却需要攻击25次才可使股票网络崩溃,即基于混合攻击策略下的随机攻击给股票网络造成的破坏程度要大于点攻击策略下的蓄意攻击,此结论在图6b中也成立。同时,从图6b中可以看出:股票网络初始的点连通率S(v)并不为1,这是由于初始股票网络中有一些孤立节点造成的。
上述研究结果表明:在攻击次数t相同的情况下,混合攻击策略的攻击效率要明显优于点攻击策略以及边攻击策略。
4 结束语
本文主要研究了基于边权重的混合攻击策略,并论证了将边权重作为边重要性度量指标的合理性及有效性,同时将混合攻击策略与点攻击策略、边攻击策略进行了比较分析。混合攻击策略下的网络鲁棒性最弱,其次是点攻击策略,而边攻击策略下的网络鲁棒性最强。
随着网络时代的蓬勃发展,新的网络攻击策略层出不穷,只有将复杂的混合攻击策略研究透彻,才能有效地保护或者破坏网络。而针对混合攻击策略下的网络保护策略,将是下一步的研究方向。
[1] 孙建,胡志华.全球集装箱海运航线网络关键港口识别[J].河南科技大学学报(自然科学版),2016,37(6):95-99.
[2] 夏昱,滕克难,高飞.舰艇编队协同反导网络关键边评估[J].兵工自动化,2013,32(7):52-54.
[3] JI X P,WANG B,LIU D,et al.Improving interdependent networks robustness by adding connectivity links[J].Physica a (statistical mechanics and its applications),2016,444:9-19.
[4] 赵焱鑫,李黎,王小明.复杂网络加边扩容策略研究[J].计算机应用研究,2015,32(6):1839-1841.
[5] ZHUO Y,PENG Y,LIU C,et al.Improving the attack tolerance of scale-free networks by adding and hiding edges[J].Physica scripta,2011,83(2):025801.
[6] BEYGELZIMER A,GRINSTEIN G,LINSKER R,et al.Improving network robustness by edge modification[J].Physica a (statistical mechanics and its applications),2005,357(3):593-612.
[7] 程明阳,陈京,张明川,等.无线传感网络中跨层传输优化策略[J].河南科技大学学报(自然科学版),2017,38(2):35-40.
[8] 黄仁全,李为民,董雯,等.不同攻击策略下作战体系网络抗毁性研究[J].复杂系统与复杂性科学,2012,9(3):62-69.
[9] GIRVAN M,NEWMAN M E.Community structure in social and biological networks[J].Proceedings of the national academy of sciences of the United States of America,2002,99(12):7821-7826.
[10] HOLME P,KIM B J,YOON C N,et al.Attack vulnerability of complex networks[J].Physical review e,2002,65(5):056109.
[11] 谭跃进,吴俊,邓宏钟.复杂网络抗毁性研究进展[J].上海理工大学学报,2011,33(6):653-668.
[12] ALBERT R,JEONG H,BARABSI A L.Error and attack tolerance of complex networks[J].Nature,2000,406:378-382.
[13] ERDOS P,RENYI A.On the evolution of random graphs[J].Publication of the mathematical institute of the Hungarian academy of sciences,1960,38(1):17-61.
[16] WATTS D J,STROGATZ S H.Collective dynamics of ‘small-world’ networks[J].Nature,1998,393:440-442.
[17] ZHUO Y,PENG Y,LONG K,et al.Improving robustness of complex communication networks by allocating redundancy links[C]//Communications and Photonics Conference and Exhibition.IEEE,2009:1-2.
[18] 吴翎燕,韩华,宋宁宁.基于相关系数和最佳阈值的股票网络模型构建[J].复杂系统与复杂性科学,2013,10(4):49-55.
国家自然科学基金项目(71372135,71140015);中央高校基本科研业务费专项基金项目(2015-zy-115)
章鹏(1991-),男,湖北潜江人,硕士生;韩华(1975-),女,山东莱州人,教授,博士,硕士生导师,主要研究方向为复杂性分析与评价、经济控制与决策等.
2017-03-14
1672-6871(2017)06-0038-06
10.15926/j.cnki.issn1672-6871.2017.06.008
TP399
A

