小升初数学衔接教学探微——以人教版七（上）应用题及几何规律题教学为例

李朝阳

（莆田砺青中学,福建莆田351100）

小升初数学衔接教学探微
——以人教版七（上）应用题及几何规律题教学为例

李朝阳

（莆田砺青中学,福建莆田351100）

针对小升初数学教学中学生感到较难的两大知识点：列方程解应用题、几何规律题进行教学研究，用比较通俗易懂的方法引导学生理解掌握七（上）中的应用题及几何规律题：配套问题可以理解为数量比问题；工程问题、行程问题可以理解为花钱问题；销售问题可以理解为方程“利润=售价-进价”；分段问题理解为真分段与假分段；点钟问题应理解为分针与时针的追及问题，而这里研究的几何规律题都与公式n（n-1）有关。

2

小升初；衔接教学；应用题；几何规律题

小学升入初中,数学学科是大多数学生转折的一个学科［1］，在应用题与规律题方面，学生尤为畏惧，往往成为小升初学生学习上的一个障碍，在教学上能给学生更好的解释总结，对学生的理解掌握有积极作用，特做了归纳总结。

一、列方程解应用题

（一）配套问题

配套问题可理解为数量关系问题。如：一批工人（w人）安排去加工某物，某物是由A、B两部份组成，一个工人一天可生产Aa个、Bb个，其中m个A、n个B组成一套，则应按排x人去生产A，求x？思考的时候我们可以把x个工人生产的A数量求出，（w-x）个工人生产的B数量求出，它们的比为m：n，即：（a·x）:［（w-x）·b］=m：n，最后列方程时把它写成积的形式：n·a·x=m·（w-x）·b，它就是一个简单的数量比问题。

（二）工程问题、行程问题

工程问题和行程问题都可以理解为花钱问题，思考模型为：小明有100元钱，今天花30元，明天花70元，就把这100元钱花完了，则30+70=100。

工程问题：一件工作甲单独做10天完成，乙单独做20天完成，甲先做2天后，甲、乙再合作天x完成，求x？可以理解为甲每天花（x+2）天，乙每天

行程问题：两地相距1000米，甲的速度50米/分钟、乙的速度40米/分钟，甲、乙相向而行，x分钟后还相距100米？可以理解为甲每天花钱50元，乙每天花钱40元，x天花了（1000-100=900）元，则可列方程：50x+40x=1000-100。花钱的问题是学生的平时自已的亲身体验，学生比较容易接受，把行程和工程问题往这方面引导可让学生更容易理解掌握。

（三）销售问题

销售问题大部分题目都可以转化成方程：利润=售价-进价。当然，这里利润=利润率×进价，售价=标价×折数/10。

例：一件衣服标价120元，打八折后卖出还有5%的利润，求衣服进价x元？

利用“利润=售价-进价”来构造方程为：利润=利润率×进价=5%x；售价=标价×折数/10=120×8/10，易得方程：5%·x=120×8/10-x，从而得解。x天，最后把钱（单位1）都花完了。则可

（四）分段问题：

分段问题分为两种：一种定义为假分段：分的几段不独立，随数量的增加所有的价格都随之改变。另一种定义为真分段：分的几段独立，随数量的增加各分段的价格是独立的。

假分段：某公园购团体票方法是：0-10人全票50元/人；10-30人团购打九折，票价45元/人；30-50人团购打八折，票价40元/人；50人以上团购打七折，票价35元/人。本班师生共同48人去公园游玩，如何购购票更合算？

分析：这种分段随着人数的增加所有人的票价都下降，是属于假分段。若用30-50人团购打八折购票，需40×48=1920元；若用50人以上团购打七折购票，购票51张，需35×51=1785元，所以购票51张（3张没用到）反而更便宜。这种分段可能出现多买反而少付款的情况，而真分段是不会出现这种情况。

真分段：某地电价的收费标准是，每个月用0-200度，0.5元/度；每个月用200-500度，超过200度的部份0.6元/度；每个月用500度以上，超过500度的部份0.8元/度。某家单月用电300度，应交电费多少？某家单月用电x度，应交电费y元？

分析：各个分阶是独立的价格，是属于真分段。300度包含两个段，前200度0.5元/度，超过200度部份（300-200=100度）0.6元/度，则收的电费是：200×0.5+（300-200）×0.6=160元。真分段才是今后我们学习的分段函数，如下：

（五）点钟问题：

点钟的分针与时针的运动可以理解成行程问题中的追及问题。因为时针与分针的速度比是1:12，时针走30°（1格），分钟走360°（12格），时间过60分钟；可以设时针走x°，则分针走12x°，而时针的1°对应时间是两2分钟。

可先求度数，再乘以2转成化成时间。

如图1：3:00后过几分钟时针与分针重合?

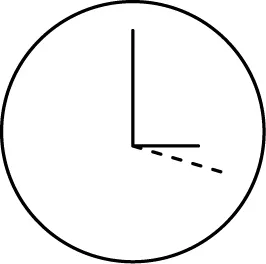
图1

分析：思考的时候可以设3:00后到时针与分针重合时时针走x°，则分针走12x°，重合时分针与时针走过的角度差为90°，则可列出方程：12x-x=90，从而很容易求出时钟与分针重合时行走的角度，再乘以2转化成时间。［2］

二、几何规律题方面

（一）有关n条直线的最多交点个数问题：（如图2）

初看“2、3、4…”与“1、3、6…”似乎看不出个所以然来，我们可以换个角度来思考：2条线最多有1个交点、3条线最多有1+2=3个交点、4条线最多有1+ 2+3=6个交点……

直线条数234n

图2 2.

（二）有关n点分得的最多线段条数问题（包括线段两端点）：（如图3）

点个数234n

可发现规律：1，1+2，1+2+3，1+2+3+…+n-1.最多交点个数：1，3，6，n（n-1）

图3

（三）有关n条射线分得的最多角问题（射线包括角两边）：（如图4）

射线条数234n

由图3可发现规律：1，1+2，1+2+3，1+2+3+…+n-1.

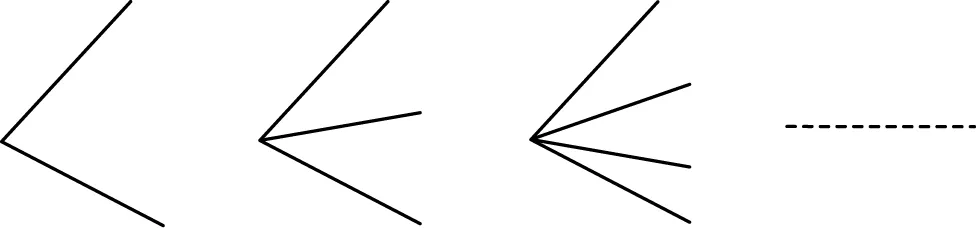
图4

观察（二）、（三）中的图示会发现，它们的数据、代数式都与（一）中的规律一样：两条线、一个交点；两点、一条线段；两条公共端点的射线、一个角，可以用一样的思路来解这类规律题。

（四）在这里有必要指出，当（二）中不包括线段两端点、（三）中射线不包括角两边时规律如何呢？我们可以把上面的数据作如下变化：（如图5、图6）

可发现规律：1，1+2，1+2+3，1+2+3+…+n-1.

所有角个数：1，3，6，分点个数（图5）

图5

其规律：1，1+2，1+2+3，1+2+3+…+n+1.

初看这个规律，发现与前面的规律不一样，其实个规律只是不包括两个端点（n少了2），所以在前面所得的规律中的n都加上2就得出代数式

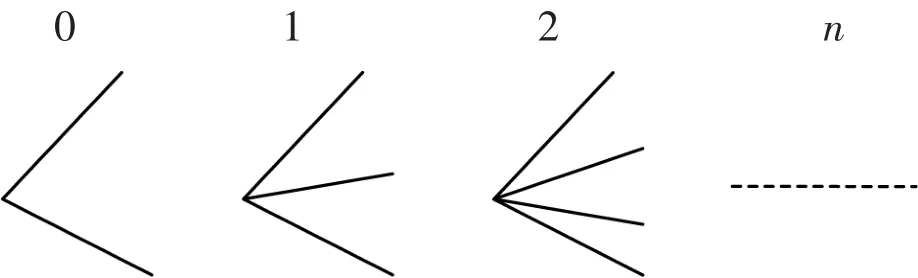
图6

这与（二）、（三）中的规律实际上只是数据对应的关系问题，前面（二）、（三）最后一个数加到（n-1），而（四）中最后一个数加到（n+1），致于思考和解答的方法都是一样的。

（五）平面上有关n刀分得的最多块饼问题：（如图7）

切饼刀数（图7）

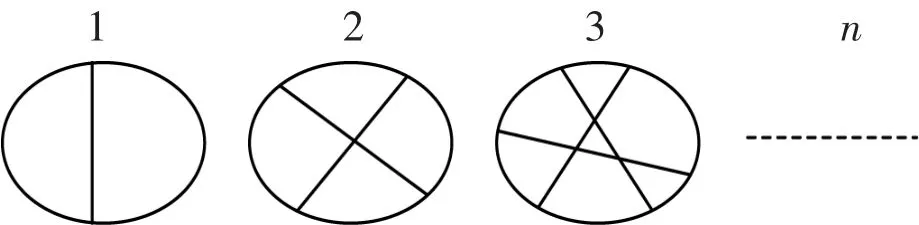
图7

规律：1，1+2，1+2+3，1+2+3+…+n+1.

所有角个数：1，3，6

规律:1+1，1+1+2，1+1+2+3，1+1+2+3+…+n.

最多分得块数

如果能先理解等差数列加法（用结对子方法理解：1+100=101；2+99=101……共结成50对，若共有奇数个数，则最后一个数单独可算半对，方法一样适用），再加上上面的图解分析，相信这些规律题就能“迎刃而解”了。［3］

最后，纵观七（上）学生觉得较难的应用题及规律题，我们在教学上可以尽可能的用他们以前学过的或生活中体验的知识或经验来解释，学生会更容易理解接受，当他们能解决这些难题，不但在初中数学学习上开了个好头，而且能大大增加他们学习数学的自信，对接下来的初中数学学习有积极的影响。

［1］陈开春.小升初数学教学衔接问题的思考［J］.中学课程辅导（教学研究），2015（1）.

［2］王海明.试析七年级列方程解应用题的瓶颈现象及对策［J］.数学学习与研究：教研版，2011（18）.

［3］李守霞.初中数学几何教学中运用模型教学研究［J］.中国校外教育（中旬），2015（2）.

G633.6

A

1673-9884（2017）06-0050-03

2017-03-10

李朝阳，男，莆田砺青中学一级教师。