基于模糊综合评价法的大学生思想道德评价模型
何敏藩,赵 飞
(1.佛山科学技术学院数学与大数据学院,广东佛山528000;2.佛山科学技术学院马克思主义学院,广东佛山528000)
基于模糊综合评价法的大学生思想道德评价模型
何敏藩1,赵 飞2
(1.佛山科学技术学院数学与大数据学院,广东佛山528000;2.佛山科学技术学院马克思主义学院,广东佛山528000)
将模糊综合评价法具体应用到大学生思想道德综合评价工作中,建立了因素集、评价集、隶属函数和权重集,实现了对大学生思想道德的综合评价。模型计算结果表明,模型能够用定量的方法分析大学生思想道德水平,具有一定的实用性。
思想道德;模糊评价;指标体系
在当今高校学生工作中,对每一个学生的思想道德要求越来越高,但德育水平不仅没有可直接测量的数量标准,而且也没有成熟的测量机制。如何客观、准确地评价学生的思想道德水平,是长期困扰学生教育与管理工作者的问题。
多年来,笔者一直在寻找对学生德育考核评价的科学方法,经过不断研究发现,作为评价对象,学生的思想道德水平本身具有模糊特征,因此尝试应用模糊数学对学生的道德水平进行评价。
在模糊数学中应用比较广泛的一种方法是模糊综合评价法,即对某一事务进行评价时常会遇到由于评价事务是由多方面的因素所决定的,因而要对每一因素进行评价;在每一因素做出一个单独评语的基础上,考虑所有因素而做出一个综合评语。本文将建立对大学生道德水平评价的三层指标体系,针对体系中的每一个指标形成调查问卷,对全国43所高校大学生进行调查,回收7 173份有效问卷后进行数据处理,然后用模糊综合评价法对大学生道德水平进行评价。
1 模糊综合评价法
模糊集合理论是由美国加利福尼亚大学的L.A.扎德教授于1965年提出的[1],他提出的概念是运用精确的数学方法,为模糊不定的现实世界和经典数学之间搭建了一座桥梁。
在我国,汪培庄教授最早提出了模糊数学的一种具体应用方法——模糊综合评价法(Fuzzy Comprehensive Evaluation)[2]。模糊综合评价法(Fuzzy Comprehensive Evaluation,FCE)对人们在评价过程中本身所带来的主观性和客观所遇到的模糊情况都能有效解决。对于受多个因素影响的目标事物,模糊综合评价法能够做出全面评价,是一种十分有效的多因素决策方法。模糊综合评价法的优点主要是容易掌握相关的计算方法,并且操作容易,模型的建立较为简单,同时能处理好多层次多因素的复杂情况,对存在模糊性、不确定性特征的事物及现象,具有强大的生命力,使用起来极为方便有效。
2 模糊综合评价法的评价过程
模糊综合评价包括建立指标因素集、建立评语集、确立评价因素的权向量和综合评价四个过程[3-4]。
2.1 建立指标因素集
模糊综合评价的第1步是建立指标因素集,即对评判对象进行层次分析,确立清晰的分级指标体系,给出评判对象的因素集和子因素集。把影响各评判对象的所有因素组成因素集B=(B1,B2,…,Bm),其中B1,B2,…,Bm为一级评价指标。对于i=1,2,3,…,m,设Ci=(Bi1,Bi2,…,Bir)是一级评价指标Bi所对应的二级评价指标组成的因素集。
用相同的方法定义二级评价指标 Cij所对应的三级评价组成的因素集 dij=(dij1,dij2,…,dijk),j=1,2,3,…,r。
2.2 建立评语集
设U=(U1,U2,…,Un)是一个评语集,U是一个全序集,即对U中任意两个评语之间总存在等级差别。典型的评语集有:U=(很好,好,一般,较差,很差),U=(优,良,中等,合格,不合格),U=(1,2,3,4(分)),U=(1,2,3,4(层次))。
2.3 确立评价因素的权向量
设W=(w1,w2,…,wm)为权向量,其中W中的元素wi,i=1,2,3,…,m,本质上是评价因素Bi对因素集B=(B1,B2,…,Bm)的隶属度。
用相同的方法得到Wi=(wi1,wi2,…,wir),其中wij,j=1,2,3,…,r,本质上是评价因素Bij对因素集Ci=(Bi1,Bi2,…,Bir)的隶属度。
2.4 综合评价
首先进行单因素评价,建立模糊矩阵R。单因素模糊评价是指单独从一个因素出发进行评价,以确定评价对象对评价集元素的隶属程度。模糊矩阵是表示有限论域上的模糊关系的矩阵。
设rij∈[0,1](i=1,2,3,…,m,j=1,2,3,…,n),矩阵R=(rij)m×n就是m×n阶的模糊矩阵。
模糊矩阵的元素必须是区间[0,1]上的实数,是因为矩阵的元素rij在实际问题中表示模糊关系R的隶属度。
rij为隶属度函数,可通过下式计算
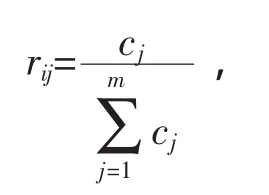
其中,cj为因素Bi,i=1,2,3,…,m,被评为第j种评语Uj的专家人数。
在确立模糊矩阵之后进行模糊综合评价。单因素模糊评价反映的是一个因素对评价的影响,而模糊综合评价则综合考查了所有因素的影响。记为:Y=W·R=(Y1,Y2,…,Ym),其中Y是模糊综合评判集,“·”一般采用普通的矩阵乘法算子。每一个评判对象结果都表现为一个模糊向量,与常规的方法不同,它包含了更丰富的信息。
用最大隶属原则来确定评判结果,就有Y=max(Yi),i=1,2,3,…,m,所对应的因素就是模糊综合评判的结果。
3 基于模糊综合评价法的大学生思想道德评价模型及计算
3.1 确立大学生思想道德水平评价的因素集和评语集
大学生思想道德水平影响因素的一级、二级、三级指标如表1所示,表1中包括指标名称、编号及其权重,因三级指标过多,所以表1中只列出指标编号及权重。

表1 大学生思想道德评价体系
A:为大学生思想道德水平;
B=(B1,B2,B3),B1:思想道德认知水平;B2:思想道德情感水平;B3:思想道德行为水平;C1=(C11,C12,C13,C14,C15,C16),C11:世界观;C12:人生观;C13:价值观;C14:政治观;C15:道德观;C16:法制观。
以此类推得到另两个一级评价指标Bi所对应的二级评价组成的因素集C2=(C21,C22),C3=(C31,C32,C33,C34,C35,C36);相应的方法定义二级评价指标Cij所对应的三级评价组成的因素集dij=(dij1,dij2,…,dijm),如d11=(d111,d112,d113),d111:对自然界的认识;d112:对社会的认识;d113:对人类的认识。
评语集U=[1,2,3,4],1:第1层次;2:第2层次;3:第3层次;4:第4层次。
3.2 确定评价指标的权重
目前,权数确定的方法主要采用专家打分法、Delphi法、AHP法。本文采取专家打分法确立各项指标权重,具体值见表1。
3.3 模糊综合评价(模型的建立、计算及结果)
(1)对三级指标做评价。即对Cij中每一个因素dijk进行评判,得出每一因素属于各种评语的程度,从而得到
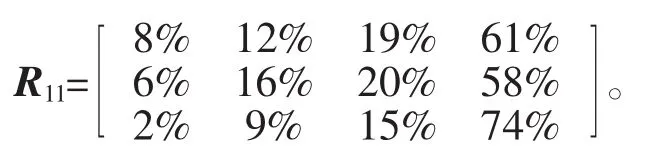
矩阵中各隶属度采用专家打分法,采用回收的7 173份有效问卷数据,对三级指标的做出各级评语的隶属度在数值上取三级指标的各层次得分比例,得分比例即调查问卷结果显示的各层得分人数与答题总人数之比,将答题总人数当作专家数,各层得分人数看作对各层打分的专家数,由专家打分法可知隶属度即为此比例值,各层次得分比例由调查问卷的数据结果得出,具体结果比例值见表1。
评价结果为
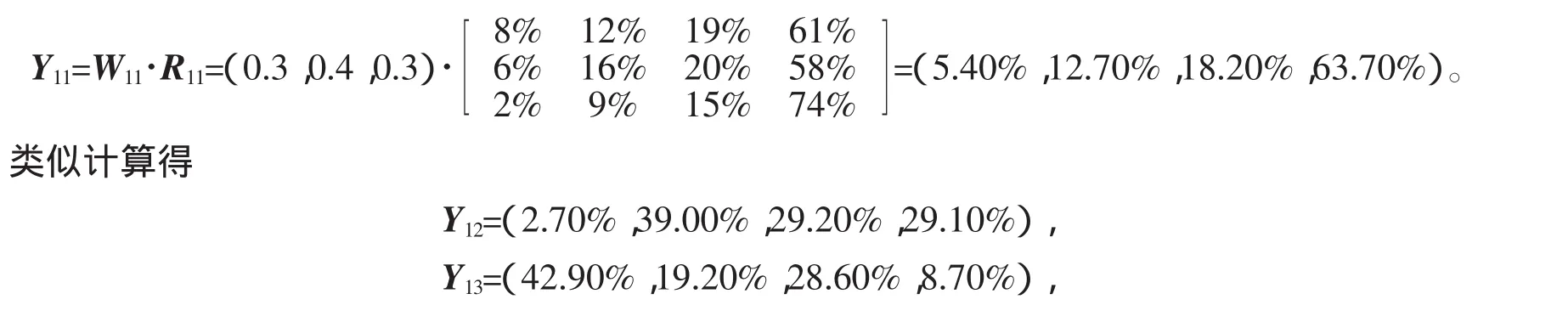

W11为d111:对自然界的认识;d112:对社会的认识;d113:对人类的认识的三个四级指标所占权重。
Y11为三级指标“世界观”的评价矩阵,也就是该指标的得分情况,即第1层次占5.40%,第2层次占12.70%,第3层次占18.20%,第4层次占63.70%。同理Y12至Y16代表C12:人生观;C13:价值观;C14:政治观;C15:道德观;C16:法制观这五个三级指标的评语情况。
(2)对二级指标做评价。

W1为C11:世界观;C12:人生观;C13:价值观;C14:政治观;C15:道德观;C16:法制观这六个三级指标所占权重。
Y1,Y2,Y3分别代表B1:思想道德认知水平;B2:思想道德情感水平;B3:思想道德行为水平这三个二级指标的评价矩阵,也就是该指标的得分情况。
(3)对一级指标(评价系统)做最终综合评价。

W1为B1:思想道德认知水平;B2:思想道德情感水平;B3:思想道德行为水平这三个二级指标所占权重。
Y为A:为大学生思想道德水平的评价矩阵,也就是该指标的得分情况。
F为最终的综合评价得分(层次)。
此结果表明,9.66%的大学生思想道德水平处于第1层次,18.74%的大学生思想道德水平处于第2层次,31.18%的大学生思想道德水平处于第3层次,40.37%的大学生思想道德水平处于第4层次。综合评级层次为3。
4 结语
本文通过问卷调查的方式确定大学生思想道德评判指标体系,采用层次分析法确定权重,建立了模糊综合评价的数学模型,给出了大学生思想道德水平的综合评价,能够用定量的方法分析大学生思想道德水平,具有一定的实用性。
接下来将尝试利用优化的方法对模型进行优化,用优化结果证明原指标体系的指标设计是否合理完备,若结果表明模型指标体系可删减指标,则进行新指标体系的建立,根据原有数据重新拟合出新的指标权重。
[1]ZADEH LA.Fuzzy Sets[J].Information and Control,1965,8:338-353.
[2]汪培庄.模糊集合论及其应用[M].上海:上海科技出版社,1983.
[3]张灵莹.定性指标评价的定量化研究[J].系统工程理论与实践,1998,18(7):98-101.
[4]张辉,高德利.基于模糊数学和灰色理论的多层次综合评价方法及其应用[J].数学的实践与认识,2008,38(3):1-6.
【责任编辑:王桂珍 foshanwgzh@163.com】
A college students’moral evaluation model based on fuzzy comprehensive evaluation method
HE Min-fan1,ZHAO Fei2
(1.School of Mathematics and Big Data,Foshan University,Foshan 528000,China; 2.School of Marxiem,Foshan University,Foshan 528000,China)
In this paper,fuzzy comprehensive evaluationmethod isapplied in the study of college students’moral evaluation.By setting up the factor sets,the evaluation sets,subjection functions and the weighting sets,the comprehensive evaluation of college students’moral is realized.Themodel results show that themodel can be used toanalyze themoral levelof college studentsquantitatively,and ithasa certain practicability.
ideology andmorality;fuzzy evaluation;index system
G641
A
2016-12-22
何敏藩(1980-),男,江西上犹人,佛山科学技术学院讲师。
1008-0171(2017)04-0031-05

