二元2n周期序列谱免疫度的快速算法
王 宁,顾 聪
(中原工学院理学院,河南郑州450007)
二元2n周期序列谱免疫度的快速算法
王 宁,顾 聪
(中原工学院理学院,河南郑州450007)
根据计算二元2n周期序列的线性复杂度的算法,给出了一个能够快速计算二元2n周期序列的谱免疫度的新算法,该算法与Games-Chan算法有相同的复杂度,能够同时求出对应的零化序列,并且举例说明了该算法的优越性。
二元序列;线性复杂度;谱免疫度;零化序列
近些年,代数攻击和快速代数攻击已经被一些密码系统广泛关注,它们对密码体制特别是对基于线性反馈移位寄存器(LFSR)的序列密码[1-2]的攻击给密码系统的安全带来了严重的威胁。攻击方法认为,如果能求解一个超定的多变元非线性方程系统,就将威胁到密码算法的安全性。因此,为了解决代数攻击的问题,人们在设计布尔函数时增加了一个新的标准——代数免疫度[3]。密码系统中,布尔函数如果具有足够高的代数免疫度,就能够有效地抵抗代数攻击。
以代数攻击的思想为依据,针对序列密码,Gong等[4]提出了快速离散傅里叶谱攻击(简称快速谱攻击)。代数攻击和快速代数攻击利用的是布尔函数低代数次数关系,而快速谱攻击则通过寻找密钥流序列的低傅里叶谱重量(即线性复杂度)关系进行攻击。特别地,当低线性复杂度的零化序列出现在密钥流序列中时,就能进行有效的谱攻击。针对于此,Gong等[4]提出了谱免疫度的概念,即密钥流序列或其补序列的(非零)零化序列的最低线性复杂度。对于过滤生成模型,Helleseth等[5]指出过滤函数的代数免疫度和密钥流序列的谱免疫度之间存在着相互的制约关系:若密钥流序列的谱免疫度较高,则其过滤函数的代数免疫度也较高,反之则不一定成立。说明在理论上,与代数攻击相比较,谱攻击具有更大的优势。
本文主要研究二元序列的谱免疫度计算问题。由于目前还无有效的关于谱免疫度的快速算法,因此只能根据定义来计算。对于2n周期的二元序列,根据Games-Chan算法[6],笔者给出了一个新算法,该算法不仅可以快速计算对应序列的谱免疫度,而且可以验证它与Games-Chan算法具有相同的复杂度。
1 预备知识
本文主要考虑二元序列s=s0,s1,s2,…,其中分量取值于二元域F2={0,1}。序列s具有周期N:存在一个正整数N满足si+N=si对所有非负整数i都成立。设定s=(s0,s1,s2,…,sN-1)。序列s的线性复杂度LC(s)定义为满足下面方程的最小正整数L

对所有大于等于L的j都成立;系数d1,…,dL属于F2;这里的加是模2加。如果s为零序列,则LC(s)= 0;否则LC(s)=生成该序列的线性移位寄存器的最小长度[7]。如果存在一个二元序列a=(a0,a1,…,aN-1)满足

则称序列a为序列s的一个零化序列。序列s的谱免疫度定义为序列s和s的补序列s+1的所有非零零化序列的线性复杂度的最小值。我们的主要任务就是找出可以快速计算序列谱免疫度的算法。

对于2n周期的二元序列s,它的零化序列a一定满足:如果si=1,i=0,1,…,2n-1,则一定有ai=0;而其他位置上的值可以任意取0或1。为了求出序列s的谱免疫度,分别计算序列s与s+1的零化序列的线性复杂度的最小值,然后从中选取最小值。为了计算序列s的零化序列的线性复杂度的最小值,采用文献[8]中的思想,用一个新的变量符号*来表示未定值。这样,s的零化序列a的通式可以表示为:对于i=0,1,…,2n-1

在序列a所有的*中,必须至少有一个*最终取1来保证a为非零序列。通过对序列a中的*进行不同的赋值来求出最小的线性复杂度。
2 新的算法
笔者根据Games-Chan算法给出一个计算谱免疫度的新算法。其实新算法是分别计算序列s和s的补序列s+1的零化序列的最小线性复杂度,从而可以求出谱免疫度。

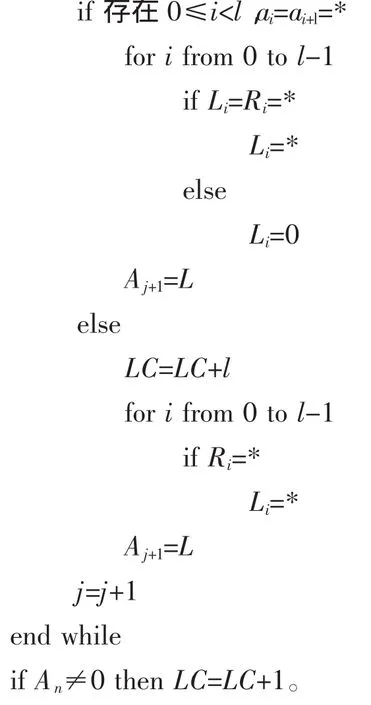
易见这个算法的复杂度与Games-Chan算法的复杂度是一样的,都为O(2n)。下面的定理证明了新算法的合理性。
定理1 上面算法是正确的。
证明 首先需注意,在序列a所有的*中,必须至少有一个*最终取1来保证a为非零序列。再根据Games-Chan算法,为了使得序列的线性复杂度尽量小,不得不尽量使得序列的左右两部分相同。所以我们的主要目标是对上述算法中序列的左右两部分的*赋值(且不能全为0)使得左右两部分相同。在第j步中,当存在0≤i<l,ai=ai+l=*时,把其他ai与ai+l只有一个为*的*都赋值为0,ai=ai+l=*时的*的赋值放到下一步再定(这两个*的值将会是一样的),这样就能保证序列左右两部分相同,并且*的值不会全为0。此时线性复杂度不会增加。当不存在ai与ai+l同时为*时,则无论对*赋何值,都不能使得序列左右两边相同,所以线性复杂度将增加l。当ai与ai+l中有一个为*时,令下一步要考虑的序列Aj+1的第i个值为*,来保证*的值根据以后的情形再确定。最后对所有非零的零化序列,一定有An≠0,根据Games-Chan算法,此时线性复杂度增加1。上面算法运行到最后,LC就是s的非零零化序列的最小线性复杂度。


3 结语
本文详细讨论了二元2n周期序列的谱免疫度的新算法。根据著名的Games-Chan算法及引入的新的变量*,给出了一个可以快速计算谱免疫度的新算法,同时还能求出对应的零化序列,并且该算法与Games-Chan算法有相同的复杂度。本文的结果具有很好的应用价值。
参考文献:
[1]COURTOISNT,PIEPRZYK J.Cryptanalysisofblock cipherswith overdefined systemsofequations[C]//Advancesin Cryptology -ASIACRYPT 2002.Berlin:Springer,2002:267-287.
[2]COURTOISN,MEIERW.Algebraic attackson stream cipherswith linear feedback[C]//Advances in Cryptology-EUROCRYPT 2003.Berlin:Springer,2003:345-359.
[3]MEIERW,PASALICE,CARLETC.Algebraic attacks and decomposition of Boolean functions[C]//Advances in Cryptology-EUROCRYPT 2003.Berlin:Springer,2004:474-491.
[4]GONGG,RONJOM S,HELLESETH T,etal.Fastdiscrete Fourier spectraattackson stream ciphers[J].IEEETransactionson Information Theory,2011,57(8):5555-5565.
[5]HELLESETH T,RONJOM S.Simplifying algebraic attackswith univariate analysis[C]//Information Theory and Applications Workshop.New York:IEEE,2011:1-7.
[6]GAMESR,CHAN A.A fastalgorithm for determining the complexity ofa pseudo-random sequencewith period 2n[J].IEEE Transactionson Information Theory,1983,29(1):144-146.
[7]RUPPELR.Analysisand Design ofStream Ciphers[M].New York:Springer-Verlag,1986.
[8]CHANG Z,WANGX.On the firstand second error linear complexity ofbinary 2n-periodic sequences[J].Chinese Journalof Electronics,2013,22(1):1-6.
【责任编辑:王桂珍 foshanwgzh@163.com】
A fastalgorithm for spectral immunity of binary 2n-periodic sequences
WANG Ning,GU Cong
(College of Science,Zhongyuan University of Technology,Zhengzhou 450007,China)
According to the algorithm for computing the linear complexity of binary 2n-periodic sequences,one new algorithm for fast computing the spectral immunity ofbinary 2nperiodic sequences is provided in this paper which can find the corresponding annihilator simultaneously,and an example is provided to show the efficiency of thisnew algorithm.
binary sequences;linear complexity;spectral immunity;annihilator
TP301.6
A
2017-03-16
河南省教育厅科研项目(13A110117)
王 宁(1976-),女,河南周口人,中原工学院讲师。
1008-0171(2017)04-0023-05

