专题研究：高中物理中的串并联问题

沈阳市第二中学　沈小冬

串并联是调节、扩大元件性能的一种方法，高中物理中除了有电阻串并联问题以外，还牵涉电容、弹簧、电源的串并联问题。本文先研究电阻串并联问题，分析其连接方式界定，电压、电流、功率等分配规律，等效值推导，高考真题解析等，再类比电阻研究方法分析电容、弹簧、电源串并联的各项规律，最终形成类比表格，有利于提高对各种串并联规律的理解。

电学、力学元件通过串并联的方式来实现性能的调节和扩大。学习过程中对电阻串并联的规律关注较多，而对电容、弹簧、电源等其他元件的串并联研究较少。当教材或高考中出现其他元件串并联问题时，学生们往往感觉力不从心，因此系统地梳理电阻串并联的研究方法是非常有必要的，再以此类比研究其他元件的串并联规律。

一、电阻

1.电阻串并联判断

（1）定义法

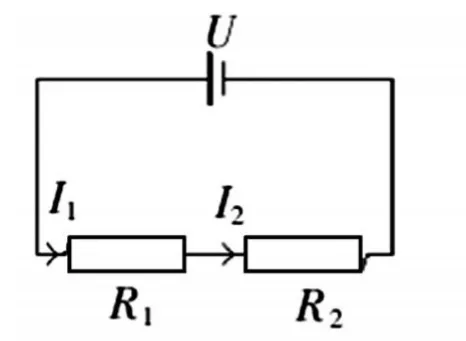
图1-1　

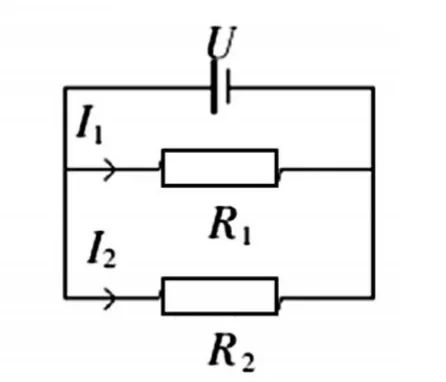
图1-2

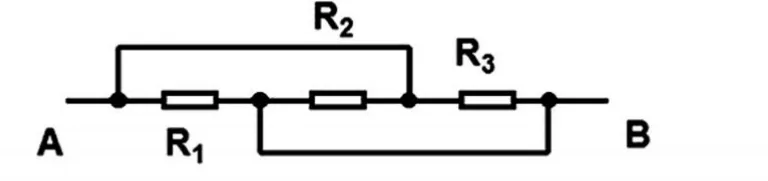
图1-3

根据串并联的定义，当把两个电阻首尾相连，接到电路中，这两个电阻就是串联，如图1-1。两个电阻两端分别连在一起，然后接到电路中，这两个电阻就是并联，如图1-2。

（2）物理法

有的电路图在画的时候，由于电阻的位置，导线的分布干扰，导致很难看清串并联关系。这时，比较适合根据串并联物理量关系，来判定连接方式。电阻串联时，通过电阻的电流相同；并联时，电阻两端的电压相同。图1-3中，三个电阻都接在φA和φB之间，所以它们属于并联关系。

2.电阻串并联分配规律

（1）串联电压、功率分配规律

根据电压U=IR，串联电路电流相同，电压的分配关系为 U1∶U2∶...UN=R1∶R2∶...RN， 电压与电阻成正比。根据电功率P=I2R，功率的分配关系为P1∶P2∶...PN=R1∶R2∶...RN，电功率与电阻成正比。

（2）并联电流、功率分配规律

3.等效电阻的规律

（1）串联

多个电阻串联，在电路中对电流的阻碍作用可等效成一个电阻，根据电阻定义，U=IR+IR，12得R串=R1+R2，电阻串联后电阻值增大。

（2）并联

多个电阻并联，在电路中对电流的阻碍作用也可等效成一个电阻，根据，得

（2）串并联机理

4.串并联机理认识

（1）影响电阻大小的因素面积电阻串联，可以理解为长度变长，由，也可以得到串联电路等效电阻规律。串联就是通过改变元件的长度来改变元件性能。

两个相同材料、相同长度电阻并联，可以理解为截面积变大，由，也可以得到并联电路等效电阻规律。并联就是通过改变元件的截面积来改变元件性能。

5.高考题分析

例1（2016年海南卷第12题）某同学改装和校准电压表的电路图如图所示，图中虚线框内是电压表的改装电路。

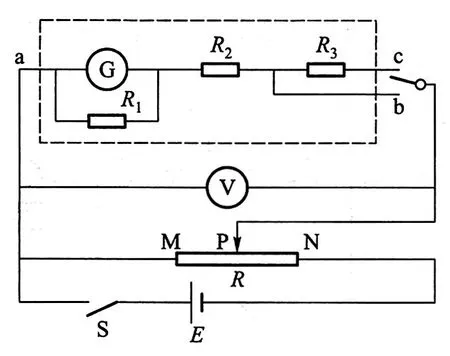
（1）已知表头G满偏电流为100μA，表头上标记的内阻值为900Ω。R1、R2和R3是定值电阻。利用R1和表头构成1mA的电流表，然后再将其改装为两个量程的电压表。若使用a、b两个接线柱，电压表的量程为1V；若使用a、c两个接线柱，电压表的量程为3V。则根据题给条件，定值电阻的阻值应选R1=____Ω，R2=____Ω，R3=____Ω。

（2）用量程为3V，内阻为2500Ω的标准电压表V对改装表3V挡的不同刻度进行校准。所用电池的电动势E为5V；滑动变阻器R有两种规格，最大阻值分别为50Ω和5kΩ。为方便实验中调节电压，图中R应选用最大阻值为____Ω的滑动变阻器。

【答案】（1）1009102000（2）50

【解析】本道高考题中，将R1和表头并联构成1mA的电流表，就是利用并联的分流效果。再将其和R2和R3串联，改装为两个量程的电压表，是利用串联的分压作用。本题还考查了两种常见控制电流中的分压式连接方式，分压式控制方法是利用混联电路的作用，实现小电阻对大电阻上电压的调节。

二、电容

1.电容串并联判断

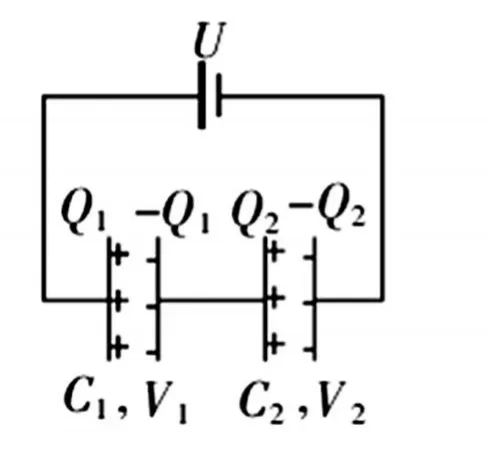
图2-1　

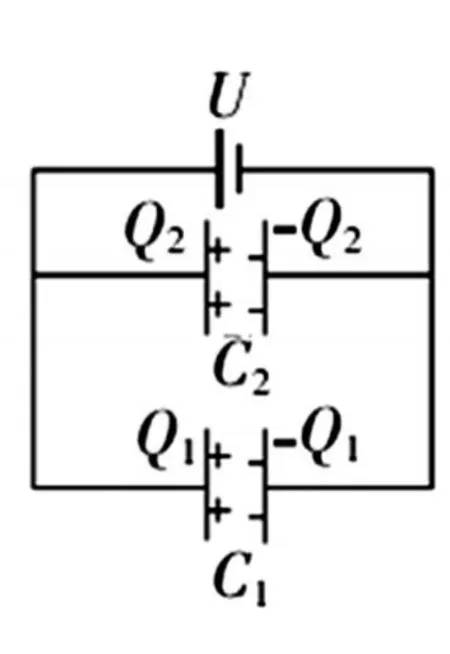
图2-2

按照串并联的定义，图2-1的电容属于串联关系，图2-2的电容属于并联关系。电容串联时，相邻电容的正极和负极连在一起，原本两极是电中性，现在电荷发生移动，所以正极和负极带电量相同。所以串联的电容带电量相同。电容并联时，电容两端电压相同。所以也可以根据电量和电压关系判断串并联。

2.电容串并联分配规律

（1）串联电压分配规律

（2）并联电量分配规律

根据Q=CU，并联电容器的电压相等，Q1∶Q2=C1∶C2，电量与电容成正比。

3.等效电容的规律

（1）串联

（2）并联

4.串并联机理认识

（1）影响平行板电容器电容大小的因素

平行板电容器电容大小跟两板的正对面积s、两板的间距d，以及板间的电介质相对介电常数εr有关，表达式为

（2）串并联机理

5.高考题分析

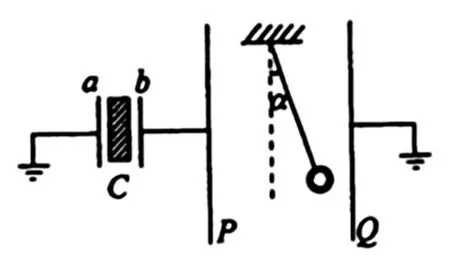
例2（2008年宁夏卷第21题）如图所示，C为中间插有电介质的电容器，a和b为其两极板；a板接地；P和Q为两竖直放置的平行金属板，在两板间用绝缘线悬挂一带电小球；P板与b板用导线相连，Q板接地。开始时悬线静止在竖直方向，在b板带电后，悬线偏转了角度α。在以下方法中，能使悬线的偏角α变大的是

A.缩小 a、b 间的距离

B.加大 a、b 间的距离

C.取出a、b两极板间的电介质

D.换一块形状大小相同、介电常数更大的电介质

【答案】BC

【解析】本题中的两个电容，很多学生从连接方式中看，误以为是串联关系，但从物理量关系可知，这两个电容属于电压相同，而不是带电量相同，所以是并联关系。并联电容，每个电容带电量与电容值成正比，题中两板电荷量Q视为不变。要使悬线的偏角增大，就是增加右侧电容带电量，即减小左侧电容带电量，所以要减小左侧电容器的电容C值。根据可知，可以增大板间距d、减小相对介电常数εr，减小板的正对面积s。也可通过等效电容来理解，要使悬线的偏角增大，就是使得电容器电压变大，并联电容电压相同，等效电容C并=C1+C2，根据，减小左侧电容值，就可以减少等效电容值，从而提高电压，增大悬线的偏角。

三、弹簧

1.弹簧串并联判断

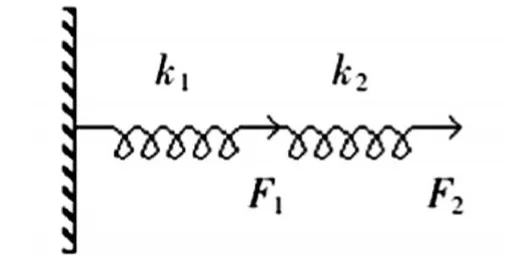
图3-1　

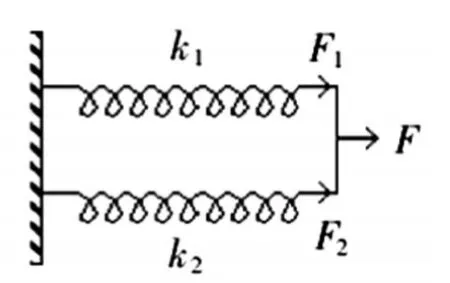
图3-2

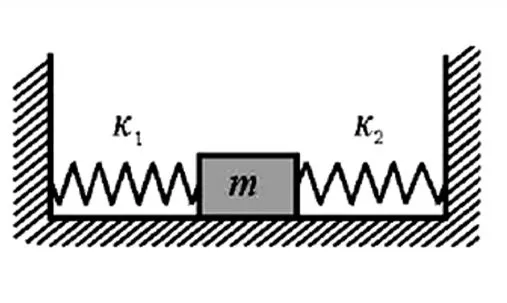
图3-3

根据定义图3-1两个弹簧为串联关系，图3-2为并联关系。串联弹簧，力相同；并联弹簧，长度变化相同。图3-3长度变化相同，共同作用于一个物体，效果等同于弹簧在一侧，是并联关系。

2.弹簧串并联分配规律

（1）串联形变量、弹性势能分配规律

根据胡克定律F=kx，串联弹簧的弹力相同，x1k1=x2k2，得，形变量与劲度系数成反比。根据弹性势能表达式，得，弹性势能也与劲度系数成反比。

（2）并联弹力、弹性势能分配规律

根据胡克定律F=kx，原长相同的弹簧并联，形变量相同，得，弹力与劲度系数成正比。根据弹性势能表达式，得弹性势能也与劲度系数成正比。

3.等效弹簧的规律

（1）串联

（2）并联

4.串并联机理认识

（1）影响弹簧劲度系数的因素

弹簧的劲度系数表示弹簧的一种属性，其大小与弹簧的材料、弹簧丝的粗细、弹簧圈的直径、弹簧的原长等因素有关，此外，弹簧所处的环境温度也对劲度系数有影响，这是由弹簧材料性质决定的。在教学和生活中经常使用的圆柱形弹簧，通常是由细丝密绕而成，其劲度系数可以近似表示为k=，G为弹簧材料的剪切模量，r为弹簧丝半径，n为有效圈数，R为弹簧的半径，有效圈数与圆柱形弹簧的原长的关系为L=2rn，因为这类弹簧是密绕而成的，带入上式可得

（2）串并联机理

两个完全相同的弹簧串联，可以理解为弹簧长度L或者理解为有效圈数n加倍，根据或，则劲度系数变为原来的一半。反之，一个圆柱形的弹簧截成两个原长相等的弹簧，那么得到的新弹簧的劲度系数比原来大，因为长度变为原来一半，所以劲度系数变为原来2倍。

5.高考题分析

例3（2014年新课标Ⅱ卷第23题）某实验小组探究弹簧的劲度系数k与其长度（圈数）的关系。实验装置如图（a）所示：一均匀长弹簧竖直悬挂，7个指针 P0、P1、P2、P3、P4、P5、P6分别固定在弹簧上距悬点 0、10、20、30、40、50、60 圈处；通过旁边竖直放置的刻度尺，可以读出指针的位置，P0指向0刻度。设弹簧下端未挂重物时，各指针的位置记为x0；挂有质量为0.100kg的砝码时，各指针的位置记为x。测量结果及部分计算结果如下表所示（n为弹簧的圈数，取重力加速度为9.80m/s2）。已知实验所用弹簧总圈数为60，整个弹簧的自由长度为11.88cm。

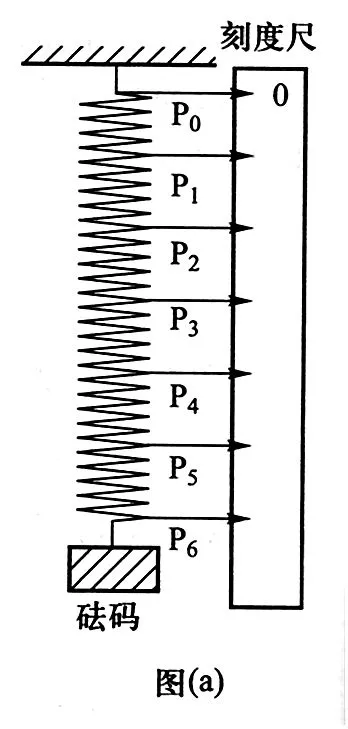
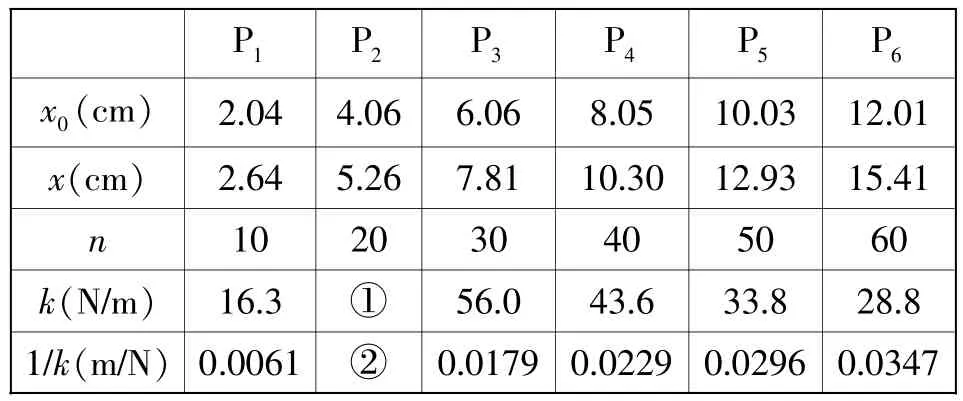
P1　P2　P3　P4　P5　P6x0（cm）　2.04　4.06　6.06　8.05　10.03　12.01 x（cm）　2.64　5.26　7.81　10.30　12.93　15.41 n　10　20　30　40　50　60 k（N/m）　16.3　①　56.0　43.6　33.8　28.8 1/k（m/N） 0.0061　②　0.0179　0.0229　0.0296　0.0347

（1）将表中数据补充完整：①____，②____。

（2）以 n 为横坐标，1/k 为纵坐标，在图（b）给出的坐标纸上画出1/k-n图像。

（3）图（b）中画出的直线可近似认为通过原点，若从实验中所用的弹簧截取圈数为n的一段弹簧，该弹簧的劲度系数k与其圈数n的关系的表达式为k=____N/m；该弹簧的劲度系数k与其自由长度l0（单位为m）的关系的表达式为k=____N/m。

【答案】（1）①81.7②0.0122

（2）略

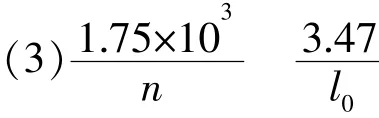
【解析】本题是实验题，目的是考查通过实验归纳找寻规律的能力。虽然只有一根弹簧，但可以理解为长短不同的6根弹簧。弹簧串联可以理解为增加长度，根据，两个相同弹簧串联，劲度系数减半，N个相同弹簧串联，劲度系数减为原来的，所以劲度系数与自由长度l0（圈数n）成反比就好理解了。

四、电源

1.电源串并联判断

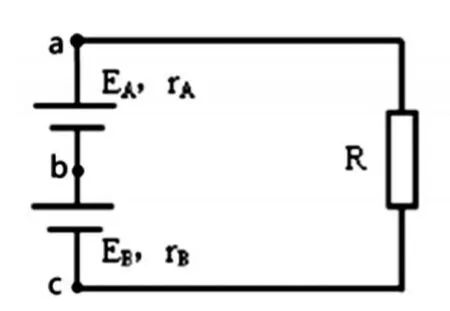
图4-1　

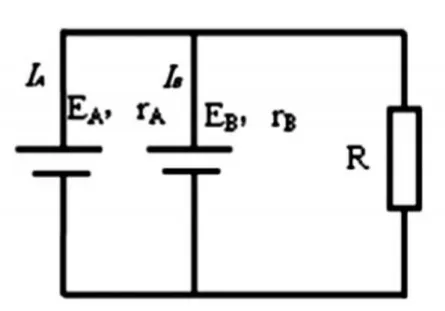
图4-2

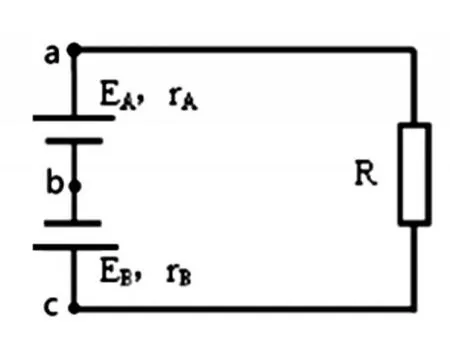
图4-3

根据定义，图4-1中两个电源是串联关系，也可通过串联电源的电流相同来判断。图4-2中两个电源是并联关系，也可通过并联电源的路端电压相同来判断。

2.电源串并联电流、电压、功率分配规律及等效电动势内阻

（1）理想恒流电源串联

恒流电源相当于内阻无穷大，两个恒流电源IA=IB=I并联，外接线性电阻元件R，如图4-1。通过电阻的电流为I，电源路端电压U=IR，这种情况等效于两个电源内阻比外电路电阻大得多，电源的能量基本消耗在内电路上。恒流电源IA≠IB串联没有事实基础，这样的物理模型没有意义。

（2）理想恒压电源并联

恒压电源相当于内阻为零，两个恒压电源EA=EB=E（rA=rB=0）并联，外接线性电阻元件R，如图4-2。电源路端电压U=E，通过负载电阻的电流这种情况等效于两个电源共同为外电路提供能量，且电源的能量消耗在外电路上，内部几乎没有能量消耗。恒压电源EA≠EB并联没有事实基础，这样的物理模型没有意义。

（3）实际电源串联

两个实际电源串联，电动势EA≠EB，内阻不为零且 rA≠rB，如图 4-1，IA=IB=I，Uac=IR，Uab=EA-IArA，Ubc=EB-IBrB，Uac=Uab+Ubc，解之得 Uac=（EA+EB）-I（rA+rB），I=。电动势等效成E=EA+EB，内阻等效成 rA和 rB串联，r等效=rA+rB。 电源总功率 P=EI，得两个电源总功率之比。

（4）实际电源并联（等电动势）

两个实际电源并联，电动势EA=EB=E，内阻不为零且 rA≠rB，如图 4-2。 U=IR，I=IA+IB，U=EA-IArA，U=EB-IBrB。解之得

电动势等效成一个电动势E，内阻等效成rA和rB并联，。电源总功率P=EI，得两个电源总功率之比。

（5）实际电源反向串联

两个实际电源反向串联，如图4-3，以顺时针为正方向。将（3）实际电源串联的推导中，方程中的EB改写成-EB， 结果得 Uac=（EA-EB）-I（rA+rB），I=。电动势等效成E=EA-EB。

3.串并联机理认识

化学电池的电动势取决于阳极和阴极材料，跟材料化学反应面积没有关系，电源并联，等效成改变反应面积，所以电动势不变。电池内阻跟材料的截面积有关，所以并联后截面积变大，等效电源的内阻减小。

导体棒切割引起的电动势大小E=BLV。双导体棒在磁场中切割，串联时可以理解成棒长变长，所以电动势变大，内阻也变大；并联时可以理解为截面积变大，电动势跟截面积无关，所以等效电动势不变，等效内阻变小。

4.高考题分析

例4（2011年海南卷第16题）如图，ab和cd是两条竖直放置的长直光滑金属导轨，MN和 M′N′是两根用细线连接的金属杆，其质量分别为m和2m。竖直向上的外力F作用在杆MN上，使两杆水平静止，并刚好与导轨接触；两杆的总电阻为R，导轨间距为l。整个装置处在磁感应强度为B的匀强磁场中，磁场方向与导轨所在平面垂直。导轨电阻可忽略，重力加速度为g。在t=0时刻将细线烧断，保持F不变，金属杆和导轨始终接触良好。求

（1）细线烧断后，任意时刻两杆运动的速度之比；

（2）两杆分别达到的最大速度。

【答案】（1）v1∶v2=2∶1

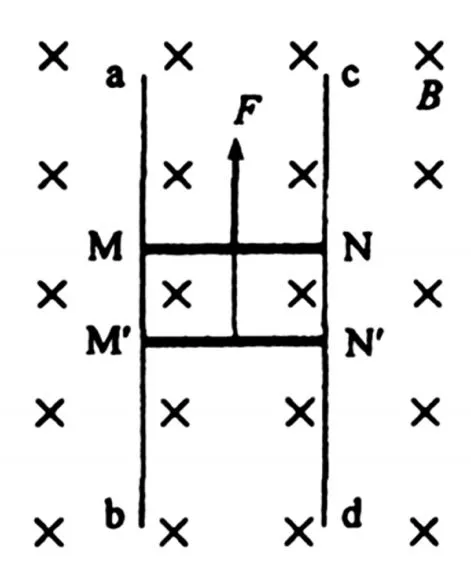
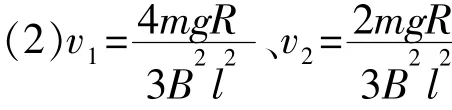
【解析】本题细线烧断后，杆MN在外力F作用下向上运动，电动势方向为逆时针，杆M′N′在重力作用下，向下运动，电动势方向也为逆时针，两个棒电动势属于同向串联，等效电动势等于E=Blv1+Blv2，等效内阻为两个电阻的和。

2016年新课标Ⅱ卷第20题，考查了法拉第圆盘发动机，如图4-4所示。圆盘切割，可以理解为半径在磁场中旋转切割，电动势，所有半径形成切割电动势属于并联关系，等效成一个半径切割的电动势。

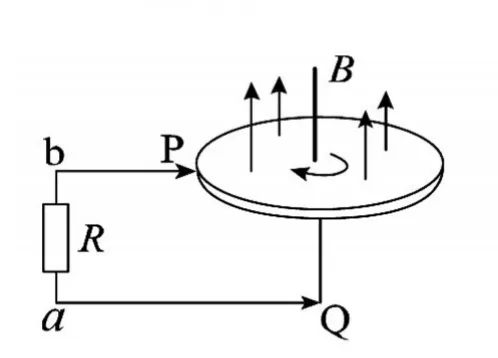
图4-4　

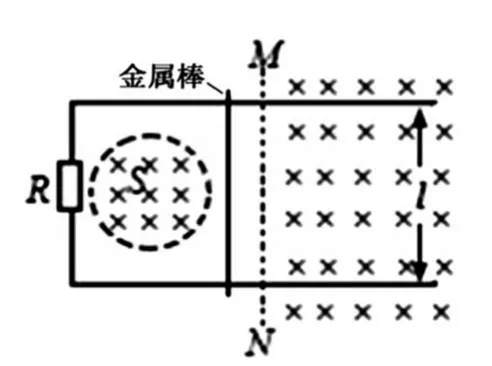
图4-5

2016年新课标Ⅲ卷第25题，考查了感生电动势和动生电动势同时存在的情况，如图4-5。瞬时感生电动势E感=ks，瞬时动生电动势E动=B0lv0，根据楞次定律和右手定则，电动势的方向相同，所以电路中的等效电动势E=E感+E动=ks+B0lv0。

五、结论

根据上述分析的结论，将电阻、电容、弹簧、电源串并联规律进行类比，总结见表1。包括串并联的相同量，分配规律，等效值等。

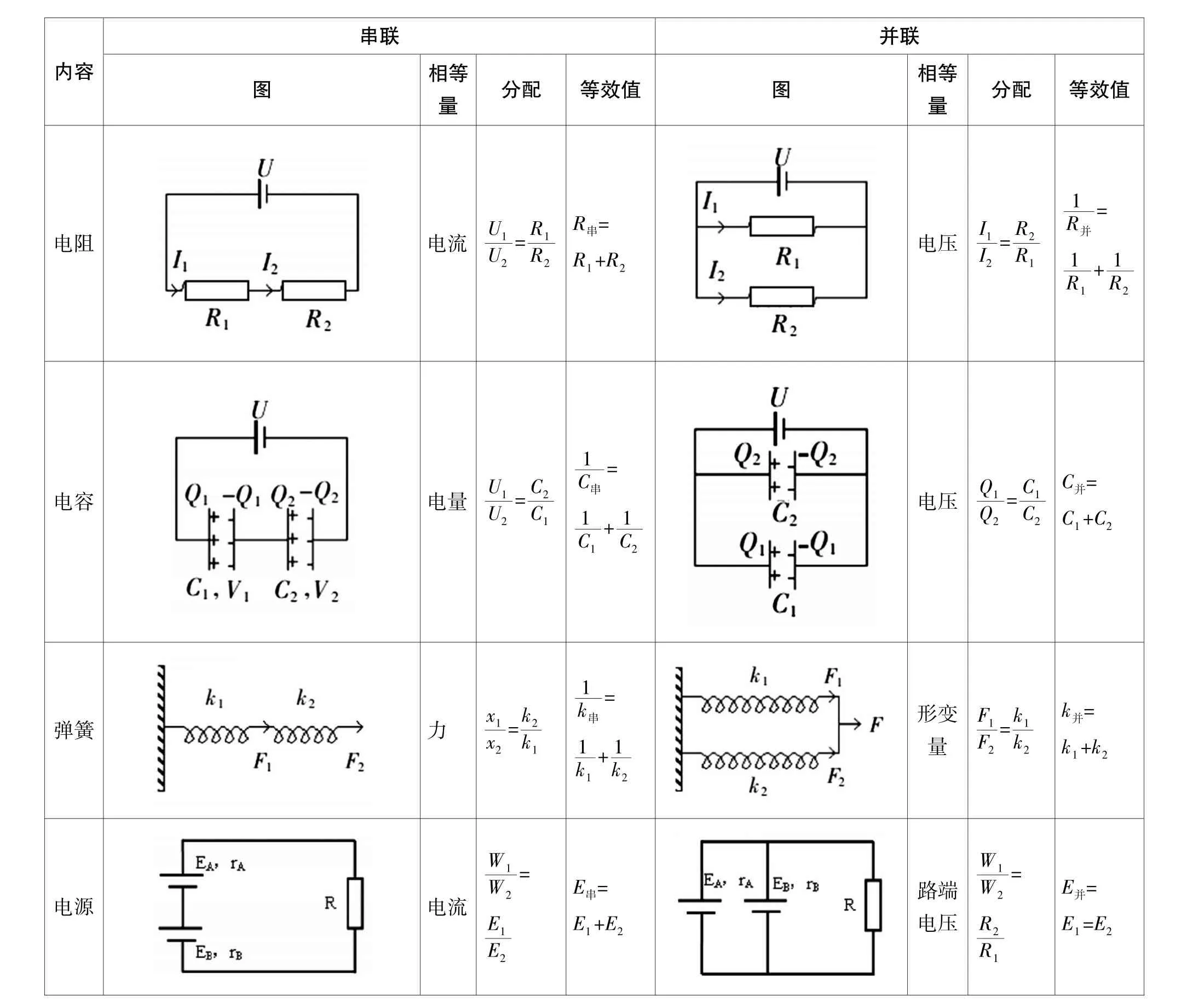
表1　电阻、电容、弹簧、电源串并联规律类比分析

通过类比，可以看出电阻、电容、弹簧、电源串并联规律有很多相似的地方，利用较熟悉的结论，启发学生掌握新的知识，有利于理解和记忆，降低难度。

以电容为例，确定串并联关系，不应只简单从结构上看电容连结方式，更应该从连结电容的相同之处入手，串联电容的带电量相同，并联电容的电压相同，这样分析有利于复杂结构或混联情况下确定串并联关系。等效值也不应停留在定义上，应该学会推导等效电容与分电容值之间的关系，可以从影响电容值因素出发，再分析串并联对其因素的影响，从而理解串并联等效值结论。平行板电容器电容值与正对面积成正比，并联电容相当于增加正对面积，所以等效电容值等于电容相加。这样有利理解串并联等效值的本质。串并联的目的，不是简单的增强或削弱功能，还具有对原有元件的调节作用。通过电容的并联，可以对原有电容上的电压和电量起到调节作用，所以，串并联不仅要研究等效值问题，还要重视、参与串并联元件间各物理的分配规律，全面理解串并联功能。