2017年高考概率统计命题趋向与应试策略
东北育才学校 王成栋
概率统计是高中数学的重要内容,它无论是在思考方法还是解题技巧上,都与高中数学其他章节有很大不同,是高中数学中相对独立的内容之一.由于概率统计和实际生活联系紧密,考查学生分析、解决实际问题的能力,所以成为每年高考必考内容之一.从近三年的高考数学新课标II卷来看,每年概率统计无论文科、理科均考查两道试题(其中一道选择或填空题,另一道解答题),分值为17分,约占总分的11%.从试题难易程度上看,概率统计在高考数学卷中属中等偏下难度,算是送分试题.
一 近三年新课标Ⅱ卷概率统计考查情况统计

年份 题号 分值 考点2014年 5 5分 条件概率19 12分 线性回归3 5分 柱状图理科2015年18 12分制作茎叶图、用样本估计总体、相互独立事件同时发生的概率2016年10 5分 几何概型、模拟试验估计π的近似值18 12分 条件概率、离散型随机变量的概率分布及期望

年份 题号 分值 考点2014年文科13 5分 古典概型求概率19 12分 茎叶图、用样本的频率估计总体的概率及总体特征分析3 5分 柱状图18 12分 制作样本频率分布直方图、用样本的特征估计总体2016年 8 5分 几何概型18 12分 样本的频率、平均值的计算2015年
通过对近三年新课标Ⅱ卷概率统计知识点的统计情况,可以看出概率统计部分的命题重点主要在以下几个方面:①概率公式;②离散型随机变量的分布列;③正态分布;④统计图,统计学的基本思想——用样本估计总体;⑤独立性检验;⑥线性回归.
概率统计中的知识点:正态分布、独立性检验、抽样方法等,在近三年新课标Ⅱ卷中还没有出现,这些都有可能会成为2017年高考数学命题的出发点,在高三复习备考中应该给予更高的重视.
二 高考概率统计试题特点
由于概率统计是实用性较强的数学知识,与现实生活联系紧密,因此每年概率统计命题视角宽阔.从全国各个不同地区高考试卷看,其中概率统计试题差异较为明显,但也有一些共性特点,它们多数都来源于生活、生产实际且具有一定的应用性和时代气息,在考查基础知识和基本方法的同时,也着重考查学生运用概率知识解决实际问题的能力、数据处理能力.
从近三年的新课标Ⅱ卷概率统计考题的侧重点来看,命题具有两方面的显著特点:
①淡化了概率计算的考查,以前常出现的“摸球”“抽取”等命题背景,在试卷中根本没出现.
②加强了统计学中统计图及用样本特征估计总体特征的考查,题目多以贴近生活的实例为载体.通过具体生活问题、生活情景,呈现题目,应用统计概率的知识解决一些实际问题.
三 高考命题趋向与应试策略
命题趋向一:概率中的两种概型、四个概率公式
高考概率小题的考查常出现在两种概型,即古典概型、几何概型;互斥事件至少有一个发生、条件概率、相互独立事件同时发生、独立重复试验等四个概率公式的应用.这些问题均属概率中的基本问题,对于这些问题的复习我们要以切实掌握基本题型的解法为主,切忌随意加深加难.
考点1古典概型
例1(2016年新课标Ⅰ卷文科)为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一花坛中,则红色和紫色的花不在同一花坛中的概率是

【命题意图】考查古典概型求概率.

1号花坛 2号花坛红、黄 白、紫红、白 黄、紫红、紫 黄、白黄、白 红、紫黄、紫 红、白白、紫 红、黄
【应试策略】枚举法是文科概率的重要方法,学生应熟练掌握.
考点2几何概型概率计算
例2(2016年新课标II卷理科)从区间0,1[]随机抽取 2n 个数 x1,x2,…,xn,y1,y2,…,yn,构成 n个数对(x1,y1),(x2,y2),…,(xn,yn),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为

【命题意图】本题主要考查几何概型的计算,利用几何概型估算π的近似值.
【解析】由题意得:(xi,yi)(i=1,2,3…n)在如图所示方格中,而平方和小于1的点均在如图所示的阴影中,由几何概型概率计算公式知,所以.故选 C.

【应试策略】几何概型问题多借助积分、线性规划等知识来考查,具有背景丰富的特点,相关知识要掌握到位.
考点3独立重复试验概率计算
例3(2015年新课标I卷理科)投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为
A.0.648B.0.432C.0.36D.0.312
【命题意图】考查独立重复试验的概率求解.
【应试策略】注意该公式与二项展开式通项的区别,所以要强化公式的记忆.
考点4互斥事件至少有一个发生与相互独立事件同时发生的概率计算
例4(2014年新课标I卷理科)4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为

【命题意图】互斥事件及相互独立事件的概率求解.
【解析】直接法:由已知,4位同学各自在周六、周日两天中任选一天参加公益活动共有24=16种不同的结果,而周六、日都有同学参加公益活动有两类不同情况:(i)一天 1 人,一天 3 人,(ii)每天各两人,共有8+6=14种方法,所求概率为,故选D.
间接法:所求事件的对立事件为4位同学均在同一天参加活动,所求概率为,故选D.
【应试策略】准确理解互斥与独立的概念及相应的加法、乘法计算公式.
考点5条件概率
例5(2014年新课标II卷理科)某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是
A.0.8B.0.75C.0.6D.0.45
【命题意图】考查条件概率的求解公式.
【解析】设A=“某一天的空气质量为优良”,B=“随后一天的空气质量为优良”,则P==0.8,故选 A.
【应试策略】准确理解条件概率的概念,熟练应用条件概率公式求解问题.
命题趋向二:统计试题常结合实际,考查抽样方法,统计图及用样本估计总体的思想
从课改地区的概率统计试题来看,试题更侧重考查统计的知识,包括统计学基本思想、抽样方法、统计图中的数据处理,独立性检验等.高考统计试题通常是通过对常见题型进行改编,通过对基础知识的整合、变式和拓展,从而加工为立意高、情境新、设问巧的实际问题,体现了当前数学试卷的设计理念,尊重不同考生群体思维的差异,贴近考生的实际,体现了人文教育的精神.
考点6样本抽样识别与计算
例6(2015年北京卷文科)某校老年、中年和青年教师的人数见下表,采用分层抽样的方法调查教师的身体状况,在抽取的样本中,青年教师有320人,则该样本的老年教师人数为
A.90B.100C.180D.300

类别 人数老年教师 900中年教师 1800青年教师 1600合计 4300
【命题意图】考查分层抽样方法.
【应试策略】简单随机抽样、系统抽样、分层抽样的共同特点是不放回抽样,且各个体被抽取的概率相等.系统抽样、分层抽样的实质分别是等距抽样与按比例抽样,只需按照定义,适用范围和抽样步骤进行,就可得到符合条件的样本.高考常结合实际应用问题,考查抽样方法.
考点7直方图
例7(2016年山东卷理科)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5 ), [22.5,25 ), [25,27.5 ), [27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是
A.56B.60C.120D.140

【命题意图】本题考查了统计与概率的知识,要求学生读懂频率分布直方图,会计算概率以及样本中有关的数据.
【解析】由题意,这200名学生中每周的自习时间不少于22.5小时的人数为200×0.7=140,故选D.
【应试策略】解决这类问题时应正确理解表中各个量的意义,识图掌握信息是解决该类问题的关键.
考点8茎叶图
例8(2008年宁夏卷理科)从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:
甲品种:271273280285285287292 294295301303303307308310314 319323325325328331334337352
乙品种:284292295304306307312 313315315316318318320322322 324327329331333336337343356
由以上数据设计了如下茎叶图
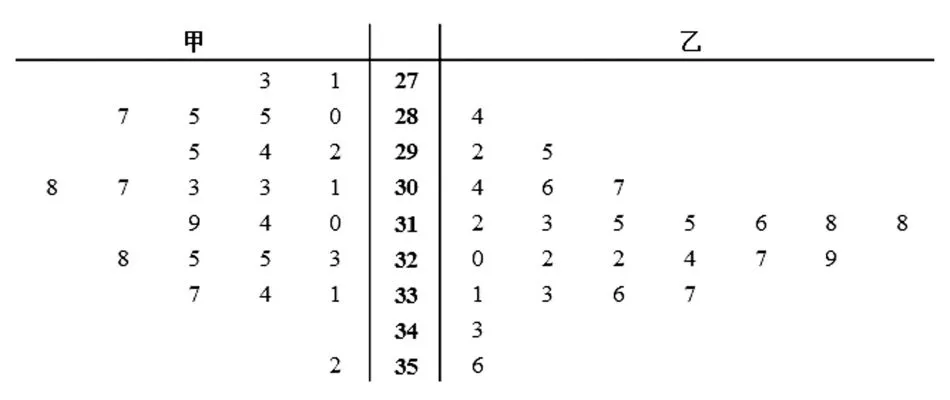
根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:
①____;②____.
【命题意图】考查学生对茎叶图特点的理解,考查学生使用茎叶图对数据的平均水平和数据稳定性分析,以及用样本估计总体的统计学思想.
【解析】1.乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度).
2.甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散[或:乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中(稳定).甲品种棉花的纤维长度的分散程度比乙品种棉花的纤维长度的分散程度更大].
3.甲品种棉花的纤维长度的中位数为307mm,乙品种棉花的纤维长度的中位数为318mm.
4.乙品种棉花的纤维长度基本上是对称的,而且大多集中在中间(均值附近).甲品种棉花的纤维长度除一个特殊值(352)外,也大致对称,其分布较均匀.
【应试策略】对用样本估计总体的统计学思想要真正做到深刻理解.
考点9平均值、中位数、方差等概念
例9(2016年上海卷理科)某次体检,6位同学的身高(单位:米)分别为 1.72,1.78,1.75,1.80,1.69,1.77,则这组数据的中位数是 _____(米).
【命题意图】考查统计中的特征量中位数.
【解析】中位数为1.76.
【应试策略】准确掌握中位数、平均数的概念,理解方差的统计含义.
考点10正态分布
例10(2015年山东卷理科)已知某批零件的长度误差(单位:毫米)服从正态分布 N(0,32),从中随机取一件,其长度误差落在区间(3,6)内的概率为
(附:若随机变量 ξ服从正态分布 N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%.)
A.4.56%B.13.59%C.27.18%D.31.74%
【命题意图】考查正态分布下的概率计算.
【应试策略】掌握正态曲线的性质,会求解正态分布下的概率.
考点11变量的相关性
例11(2015年福建卷理科)为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:

收入x(万元) 8.2 8.6 10.0 11.3 11.9支出y(万元) 6.2 7.5 8.0 8.5 9.8
A.11.4万元B.11.8万元
C.12.0万元D.12.2万元
【命题意图】考查回归直线经过样本数据中心点及利用回归直线方程做预测等.
【应试策略】要求学生要熟练掌握线性回归中的基本运算、性质、基本思想.
命题趋向三:增强应用意识,提高应用能力
目前概率统计知识已成为高考命题中应用题的热点内容,而且往往与实际问题相结合,因此对概率统计的应用题要予以重视,要培养学生认真审题的能力,在梳理知识、挖掘知识间内在联系的基础上努力提高将实际问题转化为数学模型的建模能力.
考点12离散型随机变量的分布列、期望与方差
例12(2015年广东卷理科)已知随机变量X服从二项分布 B(n,p),若 E(X)=30,D(X)=20,则p=____.
【命题意图】考查二项分布的期望和方差公式
【解析】依题可得 E(X)=np=30 且 D(X)=np(1-P)=20,解得,故应填入.
【应试策略】概率解答题属应用题范畴,试题本身难度不大,但要想顺畅作答,必须要准确理解题意,制约学生能否将概率试题答对的关键要素就在于准确地理解题干,合理地运用概率知识规范作答.
考点13独立性检验、2×2列联表
例13(2012年辽宁卷理科)电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:

将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?

非体育迷 体育迷 合计男女10 55合计
(Ⅱ)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的,求X 的分布列,期望E(X)和方差D(X).
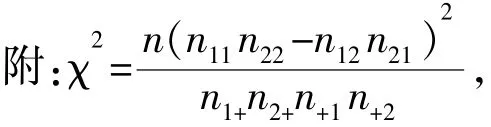

【命题意图】主要考查独立性检验的基本思想与方法,考查分析问题、解决问题的能力,试题的现实意义、实用性强,是切合考试实际的应用题.
【解析】(Ⅰ)由频率分布直方图可知,在抽取的100人中,“体育迷”有25人,从而2×2列联表如下:

非体育迷 体育迷 合计男30 15 45 45 10 55合计 75 25 100女
将2×2列联表中的数据代入公式计算,得
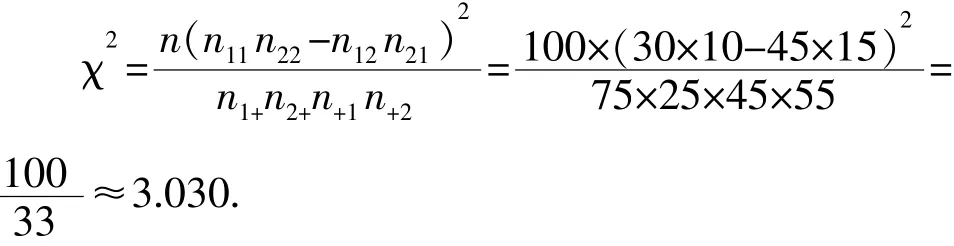
因为3.030<3.841,所以没有理由认为“体育迷”与性别有关.
(Ⅱ)由频率分布直方图知抽到“体育迷”的频率为0.25,将频率视为概率,即从观众中抽取一名“体育迷”的概率为.

X 0 1 2 3 P 27 64 27 64 91 6464

【应试策略】独立性检验是考查两个变量是否有关,并能够较精确地给出这种判断的可靠程度的一种重要统计方法,主要是通过χ2的观测值与临界值的比较解决的.利用独立性检验,能够帮助我们对日常生活中的实际问题作出合理的推断与预测.因此,在复习中要通过对统计案例的分析,理解和掌握独立性检验的方法,体会独立性检验的基本思想在解题中的应用,以提高我们处理生活和学习某些问题的能力.这类问题,一般计算量较大,在运算上要细致.
考点14统计综合解答题
例14(2016年新课标I卷理科)某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.
(Ⅰ)求X的分布列;
(Ⅱ)若要求 P(X≤n)≥0.5,确定 n 的最小值;
(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?
【命题意图】本题以实际问题为背景,以频率作为概率,综合考查柱状图(初中内容),列举法求概率,离散型随机变量的分布列、期望.
【解析】(Ⅰ)这100台机器更换的易损零件数为 8,9,10,11时的频率为分别为,故1台机器更换的易损零件数为8,9,10,11时发生的概率分别为,每台机器更换与否相互独立,X=16,17,18,19,20,21,22, 故两台机器更换易损零件个数及对应概率如下表:

8(15) 9(25) 10(15) 11(15)8(15) 16(1 25) 18( 1 25) 19( 1 25) 17( 2 25)) 17(2 25 9(2 5) 19( 2 25) 18( 4 25) 20( 2 25)10(15) 18(1 25) 19( 2 25) 20( 1 25) 21( 1 25)11(15) 19(1 25) 20( 2 25) 21( 1 25) 22( 1 25)
所为X的分布列为

X 16 17 18 19 20 21 22 P 1 25 4 6 6 5 2 25 25 25 25 25 1 25
(Ⅲ)若买19件时费用期望为

若买20件时费用期望为

可知当n=19时所需费用的期望值小于n=20时所需费用的期望值,故应选n=19.
【应试策略】概率与统计的结合是对概率统计全方位的考查,要求考生复习要全面,切勿遗漏.
考点15线性回归方程
例15(2015年新课标Ⅰ卷文科)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量 yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
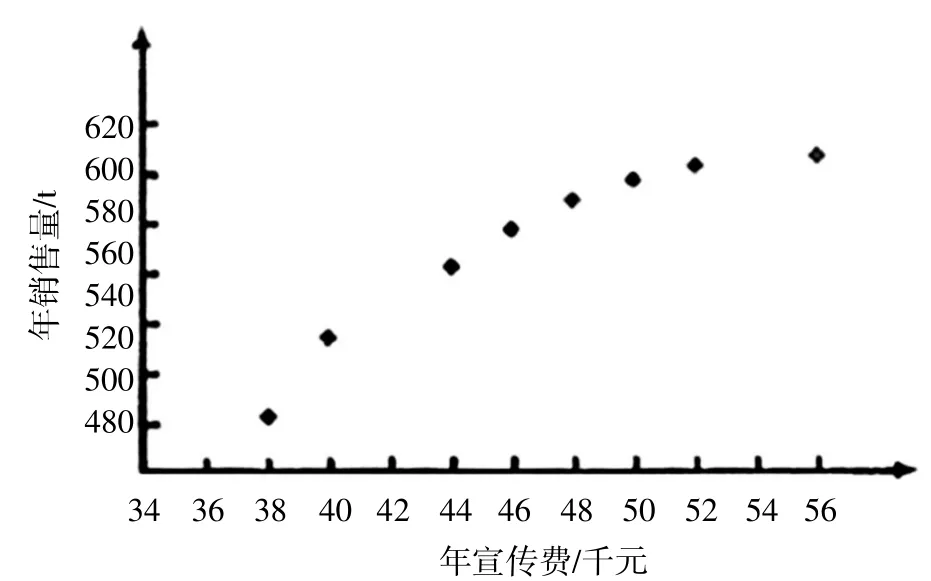

8 8∑(xi-x¯)x¯ y¯ w¯∑(xi-x¯)2 88 i=1∑(wi-w¯)i=1 i=1∑(wi-w¯)2i=1(yi-y¯) (yi-y¯)46.6 563 6.8 289.8 1.6 1469 108.8
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利润的预报值最大?

附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为

【命题意图】线性回归中的相关概念及计算.

(Ⅲ)(i)由(Ⅱ)知,当 x=49 时,年销售量 y 的预报值

年利润z的预报值

(ii)根据(Ⅱ)的结果知,年利润z的预报值

故年宣传费为46.24千元时,年利润的预报值最大.
【应试策略】了解回归的基本思想、方法及其简单应用.
四 备考方略和温馨提醒
通过以上考点回顾和分析,我们在概率统计的复习备考中需要注意以下几个问题:
方略1.高考概率统计试题属中档或中档偏下试题,因此对概率统计内容的复习一定要把握好试题难度,对于常规问题的基本解法要常抓不懈.
方略2.解答概率统计试题时,要注重阅读能力和分析问题能力的培养,重视规范解答的训练.
方略3.注重统计思想与概率、频率的整合,体现统计应用;同时注重培养学生用图表处理、分析数据的能力.
提醒1.对于概率统计中的基本概念、公式理解、记忆要准确,不似是而非.
提醒2.对概率统计中的几个基本思想如统计学的基本思想、独立性检验的思想、线性回归的基本思想理解要到位.
提醒3.对于近几年高考中的冷点问题,复习时不要掉以轻心,如条件概率、正态分布、线性回归等.
——基于Web of Science核心数据库(1975-2019)的知识图谱分析

