基于模糊估计的可调分数阶PID控制器设计
黄 博,丁跃浇,邹俊超
(1.湖南理工学院 信息与通信工程学院,湖南 岳阳 414006;2.湖南理工学院 机械工程学院,湖南 岳阳 414006)
基于模糊估计的可调分数阶PID控制器设计
黄 博1,丁跃浇2,邹俊超1
(1.湖南理工学院 信息与通信工程学院,湖南 岳阳 414006;2.湖南理工学院 机械工程学院,湖南 岳阳 414006)
可变分数阶微分环节直接影响分数阶PID控制器性能,设计分数阶PID控制器需要根据被控对象传递函数凭经验调整微分阶次。采用Oustaloup间接离散法数字实现分数阶微积分,再基于模糊估计由特定分数阶次近似得到任意分数阶次微积分环节,根据参数整定规则确立各环节系数,设计了一种可调分数阶次的PID控制器。仿真实验证明,此方法得到的微积分环节对控制系统性能没有影响,根据整数阶被控对象传递函数调节微分阶次,分数阶PID控制器有较好的控制效果。
分数阶PID;可变分数阶微分;分数阶微分近似;模糊估计
0 引言
PID控制是控制工程中应用最广泛的控制方法。分数阶PID控制则是建立在分数阶微分理论上的一种应用研究。
常分数阶微分的理论和应用研究目前已有很多研究成果,而对于时变分数阶微分的研究则是一个较新的领域。文献[1-2]从分数阶微分定义出发,对不同定义下的时变分数阶微分进行了公式推导;文献[3-5]对时变分数阶微分在实数阶和复数阶下的近似做了研究,提出了带记忆全局反馈估计、不带记忆自反馈估计、带记忆零极点增益估计等多种近似方法;在变分数阶微分应用研究上,文献[6]设计了一种基于变分数阶微分的动力学控制器,文献[7]提出了一种变模式扩散过程的变分数阶微分方程求解方法,文献[8]针对机械臂控制,设计并实现了一种离散时间变分数阶PD控制器。
在以上研究基础上,根据时变分数阶微分理论,从应用角度出发,考虑到设计和实现分数阶PID控制器需要对分数阶微积分环节做近似处理以及对控制器参数进行整定,当根据被控对象传递函数凭经验确定控制器的微积分阶次时,设计复杂度较小;当被控对象受扰动或延时而使传递函数发生变化,凭经验无法确定控制器微积分阶次时,设计的复杂度就开始加大,因此可以设计一种可调分数阶次的PID控制器来实现控制所需的任意阶次微积分环节,这些可基于模糊估计的方式由特定阶次微积分环节近似得到,根据参数整定规则得到其余参数,从而可根据被控对象传递函数设计出所需的分数阶PID控制器。
1 分数阶PID控制
分数阶PID控制的研究基础是分数阶微积分理论,较著名的PIλDμ控制最早是由PODLUBNY I教授于20世纪90年代提出的,其比整数阶PID控制多出两个可控参数,即分数阶积分阶次λ和分数阶微分阶次μ,研究表明对于同一类被控对象分数阶PID控制比整数阶PID控制性能更优。
1.1 分数阶微积分理论

(1)
式中:a、t为算子上下界,α为微积分阶次,(α)为阶次α的实部。
分数阶微积分目前没有一个统一的定义,其中最著名的是Grünwald-Letnikov(G-L)定义和Riemann-Liouville(R-L)定义。

(2)
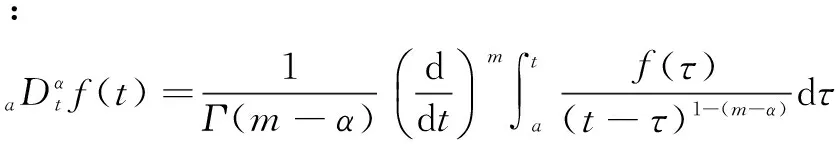
(3)
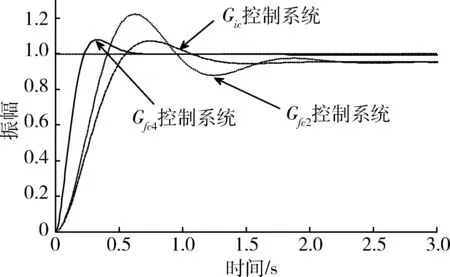
式中:m-1<α 通过引入分数阶微积分算子,微分和积分定义被统一起来。在工程中还常通过Laplace变换将时域范围内分数阶微积分引入到复频域范围内,如信号f(t)在t=0时的α阶微分Laplace变换式可表示为: L{Dαf(t)}=sαF(s),α∈R+ (4) 1.2 PIλDμ控制 分数阶PID控制系统如图1所示,其中R(s)为系统输入、Gfc(s)为分数阶PID控制器传递函数、E(s)为系统误差、U(s)为控制器输出、G(s)为被控对象传递函数、Y(s)为系统输出,分数阶PID控制器的传递函数可表示为: (5) 图1 分数阶PID控制系统框图 其中kp,ki,λ,kd,μ分别为比例系数、积分增益、积分阶次、微分增益和微分阶次,λ>0,μ>0。 在t=0时,控制器输出u(t)与系统误差e(t)有如下关系: u(t)=kpe(t)+kiD-λe(t)+kdDμe(t) (6) 被控对象输入u(t)与输出y(t)通过Laplace变换可表示其传递函数为: (7) 其中0≤α1<α2<…<αn,(an,bn)∈R, 0≤β1<β2<…<βn。 对于单个微积分传递函数形如: G(s)=sα,α∈R (8) 令s=jω,其幅频特性可表示为: (9) 相频特性可表示为: (10) 因此,其幅频特性曲线为一条斜率是20α的斜线,相频特性曲线是一条幅值为απ/2的横线。 1.3 分数阶微分的近似 要实现传递函数中分数阶微积分环节就必须将其近似成整数阶微积分环节。近似方法主要有直接近似法和间接近似法。其中Oustaloup间接近似法近似精度较高,其主要针对微积分环节,形如: G(s)=sα (11) 不考虑高低频段,在频率段(ωl,ωh)内,令其零点极点个数都为N,则其传递函数可近似为 (12) 其中 (13) (14) (15) Oustaloup近似法在MATLAB/Simulink中已有程序可以实现,本文主要采用此方法对特定阶次微积分环节进行数字实现。 模糊逻辑主要由隶属度、模糊规则、模糊推理等组成,隶属度函数值可以是0~1之间的任意数,制定模糊规则并根据隶属度可以进行模糊推理。 本文选取典型的三角隶属度函数来进行可调分数阶微积分环节的模糊近似,其曲线如图2所示(图2所示为横轴区间位于[-1,1]的11段隶属度曲线)。 图2 三角隶属度函数曲线 在分数阶PID控制器中,微积分环节输出与误差输入有如下关系: uα(t)=Dαe(t) (16) 假设有n个微积分环节: uαk(t)=Dαke(t),k=1,2,…,n (17) 并有n条模糊规则Ak(k=1,2,…,n): (18) 如果α是αk,很明显对于模糊规则“ifαisαk,Thenuα(t)=uαk(t)=e(t)sαk”的隶属度值为1,因为n条模糊规则里只有这一条是完全为真的。如果αk<α<αk+1,那么有两条模糊规则的隶属度值不为0,从而可以得到: uα(t)=μAk(α)uαk(t)+μAk+1(α)uαk+1(t) (19) 将其总结还可得到: (20) 在MATLAB/Simulink中仿真并实现此种近似方法,并设计PIλDμ控制器,其系统框图如图3所示。 图3 可调分数阶PID控制系统框图 其中模糊估计微积分环节内部框图如图4所示。 图4 模糊估计分数阶微分环节框图 上述方法主要对阶次区间位于[-1,1]的微积分环节进行模糊估计,针对任意阶次的微积分环节只需对阶次取整,令α=α1+α2,α1∈Z,-1<α2<1,对α2模糊估计即可。 对微积分环节近似后,仍需根据参数整定规则确定比例、积分和微分环节系数,对于一类典型的整数阶被控对象,其传递函数表示为: (21) 按照文献[9]给出的整定步骤,对于被控对象传递函数G(s)和控制器传递函数Gfc(s),系统的幅值裕量Am和相位裕量φm应满足式(22)和式(23): (22) φm=arg[G(jωg)Gfc(jωg)]+π (23) 其中ωp和ωg分别应满足以下条件式: (24) arg[G(jωp)Gfc(jωp)]=-π (25) 控制器传递函数满足式(26)~(29): (26) (27) (28) (29) 其中 (30) (31) 根据被控对象传递函数,期望的幅值裕量Am和相位裕量φm都是已知,对于剩余参数可根据误差平方最小化决定,即: (32) 此时kp、ki、kd可由下列关系式确定: (33) (34) (35) 依照经验确定λ和μ后,ωp和ωg则可根据以下条件确定: (36) 针对一类整数阶传递函数 (37) 文献[10]中分别设计了整数阶PD控制器和分数阶PD控制器,传递函数为: Gic(s)=20.5+2.734 3s (38) Gfc1(s)=20.5+3.734 3s1.15 (39) 根据参数整定规则,选取φm=π/4,Am=1.5。调整微分阶次令μ=1.03,得kp=16.9,则另一分数阶PD控制器的传递函数为: Gfc2(s)=19.6+4.121 6s1.03 (40) 二者的分数阶PD控制系统阶跃响应曲线如图5所示。 图5 分数阶PD控制系统阶跃响应曲线 从图5中曲线能看出经过阶次调整的控制系统Gfc2比Gfc1超调量更小,但二者由于都没有积分项,因此系统稳态误差都不为0,未达到控制要求。 针对此被控对象,仍采用上述期望的幅值相位值来设计分数阶PID控制器,令λ=0.7、μ=1.25,可以得kp=233.702 8、ki=21.990 2、kd=19.638 7,其传递函数为: Gfc3(s)=233.702 8+21.990 2s-0.7+19.638 7s1.25 (41) 调整微积分阶次,采用文献[11]中的参数,令λ=0.2、μ=1.05,得kp=138.18、ki=2.89、kd=12.38,设计另一种分数阶PID控制器,其传递函数为: Gfc4(s)=138.18+2.89s-0.2+12.38s1.05 (42) 二者的分数阶PID控制系统阶跃响应曲线如图6所示。 从图6中可以看出,Gfc4控制系统和Gfc3控制系统的稳态误差都接近0,但前者的响应速度更快,超调量更小,达到稳态的时间更短。 图6 分数阶PID控制系统阶跃响应曲线 用Gic、Gfc2、Gfc4分别对被控对象进行控制,可得系统阶跃响应曲线如图7所示,图7中可见分数阶PID控制器的控制效果最佳,响应时间最短,超调量最小,达到稳态时间也最短,分数阶PD控制器次之,整数阶PD控制器最差。 图7 整数阶与分数阶控制系统阶跃响应曲线 图8表明,分数阶与模糊估计的分数阶PID控制系统性能几乎相同,因此可以推断模糊估计近似得到的微积分环节对控制器的影响也没有改变,近似精度与未模糊的微积分环节几乎相同。 根据可变分数阶微积分在PID控制中的应用,本文提出基于模糊估计设计的可调分数阶次的PID控制器,仿真实验证明了此种控制器具有较高近似精度,根据被控对象可以任意调整微积分阶次,达到了所需的控制要求。按照此方法可以考虑设计开发一种分数阶PID控制软件,应用于诸如文献[12-13]中涉及的供热控制、换热站控制等设计复杂、控制要求较高的工业系统。 [1] OUSTALOUP A, LEVRON F, MATTHIEU B, et al. Frequency-band complex noni-nteger differentiator: characterization and synt-hesis[J]. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, 2000, 47(1): 25-39. [2] OUSTALOUP A, MATTHIEU B, LANUSSEP. The CRONE control of resonant plants: application to a flexible transmission[J]. European Journal of Control, 1993, 1(2): 275-283. [3] VALERIO D, COSTA J. Variable order fractional controllers[J]. Asian Journal of Control: Affiliated with ACPA, the Asian Control Professors’ Association, 2013, 15(3): 648-657. [4] VALERIO D, VINAGRE G, DOMINGUES J, et al. Variable-order fractional deriva-tives and their numerical approximations-I: real orders[C]. Symposium on Fractional Signals and Systems, Caparica, 2009. [5] VALERIO D, VINAGRE G, DOMINGUES J, et al. Variable-order fractional deriva-tives and their numerical approximations-II: complex orders[J]. Signal Processing, 2011, 91(3): 470-483. [6] SOON C. Dynamics with variable order op-erators[D]. Hawai’i: University of Hawai’i, 2005. [7] UMAROV S, STEINBERG S. Variable order differential equations and diffusion process-es with changing modes[J]. Zeitschrift Fur Analysis Und Ihre Anwendungen, 2009, 28(4):431-450. [8] OSTALCZYK P, BRZEZINSKI D, DUCH P, et al. The variable fractional-order discrete-time PD controller in the IISv1.3 robot arm control[J]. Central European Journal of Physics, 2013, 11(6): 750-759. [9] 赵春娜,李英顺,陆涛.分数阶系统分析与设计[M]. 北京: 国防工业出版社, 2011. [10] PODLUBNY I.Fractional-order systems and PIλDμcontrollers[J]. IEEE Transtractions on Automatic Control, 1999, 44(1): 208-214. [11] 薛定宇,赵春娜.分数阶系统的分数阶PID控制器设计[J]. 控制理论与应用, 2007, 24(5): 771-776. [12] 许青松,高经伍,刘冰,等.模糊自适应PID控制器在集中供热系统中的应用[J]. 微型机与应用, 2011, 30(17): 76-78. [13] 梁涛, 马爱龙, 张健,等.具有远程监控功能的换热站自动控制系统[J]. 电子技术应用, 2007, 33(10):93-96. Design of adjustable-order fractional PID controller based on fuzzy approximation Huang Bo1, Ding Yuejiao2, Zou Junchao1 (1. School of Information and Communication Engineering, Hunan Institute of Science and Technology, Yueyang 414006, China;2. Department of Mechanical Engineering, Hunan Institute of Science and Technology, Yueyang 414006, China) In this paper, considering the influence of variable-order fractional derivatives on fractional PID controller’s performance, a fuzzy approximation based on Oustaloup approximation is proposed to implement an adjustable-order fractional PID controller with numerical tuning methods. The simulation results show few impact of the fuzzy-approximation-based derivatives on the system and a good performance of fractional PID controller on integer system. fractional PID; variable-order fractional derivatives; approximation of fractional-order derivatives; fuzzy approximation TP273 A 10.19358/j.issn.1674- 7720.2017.12.002 黄博,丁跃浇,邹俊超.基于模糊估计的可调分数阶PID控制器设计[J].微型机与应用,2017,36(12):4-7,12. 2017-01-21) 黄博 (1990-),男,硕士研究生,主要研究方向:时滞系统、远程控制、分数阶PID。 丁跃浇(1967-),通信作者,男,硕士,教授,主要研究方向:工业控制与智能控制技术。E-mail:yjding@163.com。 邹俊超(1993-),男,硕士研究生,主要研究方向:工业自动化、控制软件开发、分数阶PID。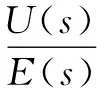
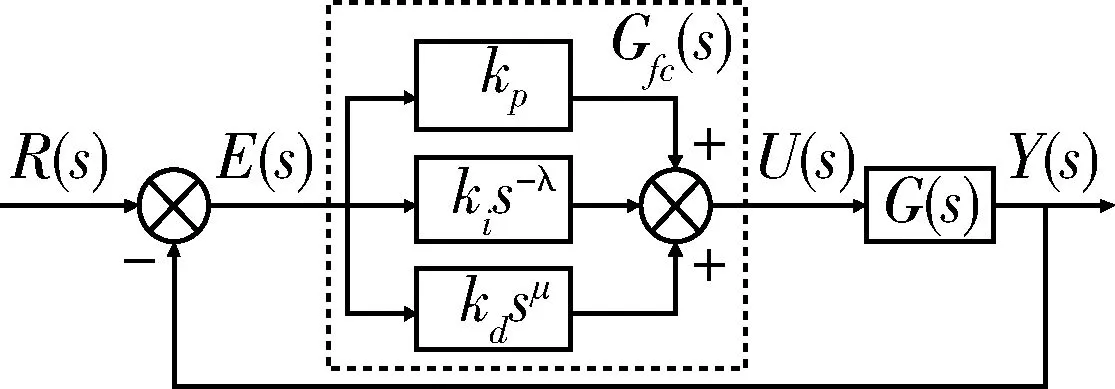




2 可调分数阶PID控制器设计

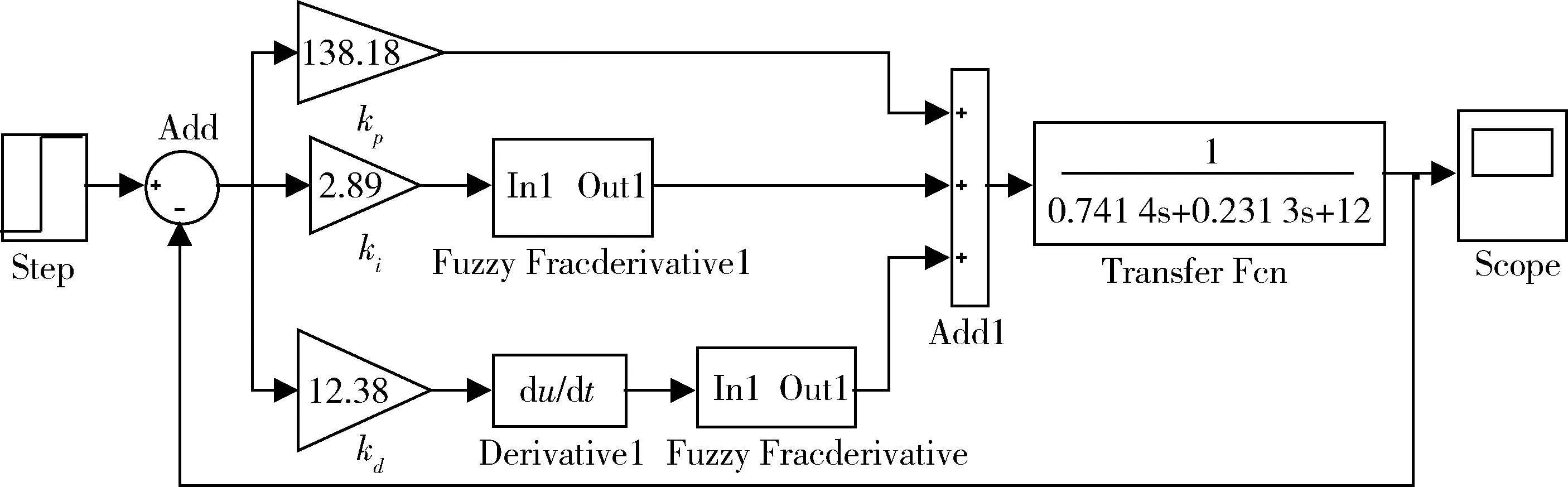


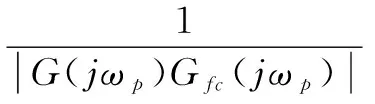
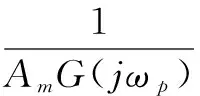
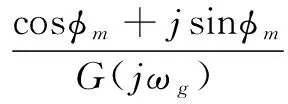

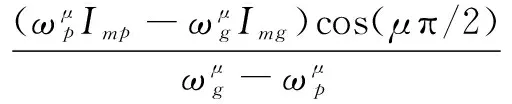


3 仿真实例




4 结论

