“小题大做”

浙江省宁波市第四中学 (315016) 蒋亚军

“小题大做”

浙江省宁波市第四中学 (315016) 蒋亚军

波利亚说过“一个专心的认真备课的老师能够拿出一个有意义但又不太复杂的题目，去帮助学生发掘问题的各个方面，使得通过这道题，就好像一道门，把学生引入一个完整的理论领域.”笔者在学考考前模拟中设计了一道数量积的试题，未曾想，竟与4月10日刚刚结束的2017年浙江省学考第22题类似.

1 考题呈现

图1

2 一题多解

这两题考查的都是数量积的知识点，而向量是沟通代数、几何与三角函数的一种工具，数量积恰好位于知识点的交汇处，所以对它深入的研究和挖掘就显得很有必要.处理平面向量数量积问题通常有定义法，坐标法，投影(几何意义)法和极化恒等式四种方法.一题会解这样是否就够用了呢？答案肯定是否定的，会一种方法那叫浅尝即止，当我们调动所学知识，在知识的交汇处将知识模块串起来，将数学方法串起来，这样才能打开学生的数学视角，培养学生的创新思维，提高学生的数学能力，让学生真正觉得数学是自然的，数学是有趣的.

2.1 建系坐标化的视角

图2

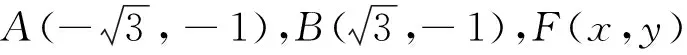
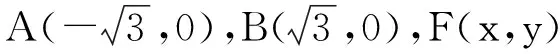
评注:学生习惯于把数量积问题转化为坐标来解决，而建系是基于计算方便的考虑，常见建系方式如上面的解法，通过坐标表示，将问题转化为函数求值域问题，根据F的位置限制，得到对应坐标的范围，从而得出结果.

2.2 三角代换的视角

既然与圆有关，那能否利用圆的参数方程(三角代换)来解决这个问题呢？

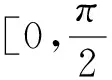
2.3 余弦定理以及基本不等式的视角

2.4 等面积的视角

评注:通过等面积法将所求目标转化为“定”底“变”高的三角形的高，随着F的改变带动hF的变化，将抽象的代数问题转化为直观的几何问题，简洁明了.

图3

2.5 极化恒等式的视角

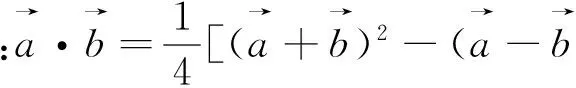
图4

2.6 合情推理(特殊值验证法)的视角

点评:此法应对选择填空有时可以起到秒杀的作用，应对大题显得不够严谨，但是巧算巧解体现了学生的创新思维，应给予肯定和鼓励.

3 一题多变

3.1 将P限制条件去掉，改成P在外接圆上任意一点，有了前面的视角和方法处理起来更为方便.

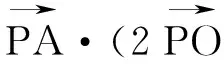
图5

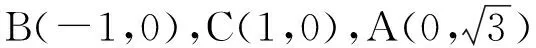
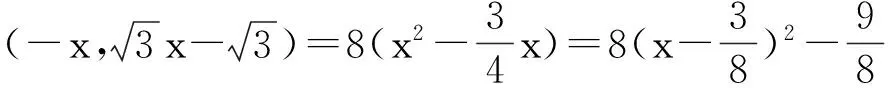
图6

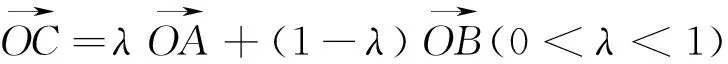
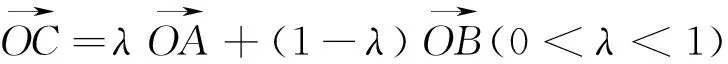
评注:由以上变式发现处理平面向量数量积问题时，如果出现的是同起点的类型，应用极化恒等式可以起到简化作用，当然坐标表示、定义和投影也都是可以选择的方法，就留给读者去完成，去品味.在有多种方法可以选择的时候，考验的是一种数学能力，如何选择熟悉的、简洁的方法来科学的处理一类题，从一题多解走向多题一解.

4 总结提升

罗增儒教授曾说：“数学解题无禁区，数学教学有讲究.”有意识的积累“知识链、方法链”，我们常说的“举一反三”“触类旁通”不就落到了实处[1]？能根据教材内容、学生实际、高考能力要求改编和精选一些有针对性的训练题，让学生经历从记忆模仿到探索发现的过程，关键在探索发现，将相互看似“独立”的知识有机的结合起来，这样，我们的“小题大做”就可充分发挥它的功能.

[1]岳建良,邱山.发散提升理解回归促进掌握[J].中学数学教学参考，2012(5)：26-29.