存在误差的层次分析法与银行国际化中的区位选择*

● 刁 莉 邓振兴 胡 娟

(1,2,3 武汉大学经济与管理学院 武汉 430072)

存在误差的层次分析法与银行国际化中的区位选择*

● 刁 莉1邓振兴2胡 娟3

(1,2,3 武汉大学经济与管理学院 武汉 430072)

本文主要研究了层次分析法(AHP)对银行国际化经营区位选择的决策的应用。当应用该方法进行区域选择决策时，准则层可包括经济一体化程度、东道国市场机会、东道国进入管制和东道国银行能力等因素。由于银行的决策是集体决策，而且对影响银行国际化因素的相对重要性的判断需要依据客观因素，有多种可能导致出现遗漏重要影响因素和判断矩阵设定存在误差的情况。当层次分析法存在误差时，在某些条件得到满足时，虽然总排序向量会有所差异，但最优决策不受影响。如果这些条件不能满足，则银行将可能不会作出最优决策。但是银行可以通过提高决策能力和应用层次分析法的技巧来减少误差，以使决策趋于最优。

层次分析法 误差 银行国际化 目标国

1.引言

后危机时代，伴随世界经济的发展，经济金融全球化的大趋势没有改变。这个时期的特点是伴随着国际金融监管改革进一步推进，大型银行在更为严格的要求下继续在全球金融业范围内进行国际化和综合化的重构；打造资产、业务和经营地域网点多元化的国际化银行，仍然是未来全球金融机构发展的主要趋势。在英国《银行家》杂志排行榜上排位靠前的银行多数都成为了全球性银行，更多的银行正在实施国际化战略。包括中国在内的一些新兴资本市场国家目前具备了很多银行国际化的有利因素，尤其是2008年以后银行的盈利水平提升，促进了中国及一些新兴资本市场国家银行国际化发展的实施。

大型银行国际化重要的问题之一就是在国际化过程中子银行的区位选择问题。本文尝试利用不同的角度：即通过减少银行管理层决策的失误来提高银行国际化选址的效率问题。具体与其他研究不同的是，本研究主要借助管理决策中的“层次分析法”来进行研究，提出了“带误差的层次分析法”。

关于银行国际化过程中的区位选择问题，一般都要经历三个阶段：选择目标市场、选择区域、选择具体城市地点；目前有较多的文献涉及这一主题。Brealey and Kaplanis(1996)以涉及37个母国和82个东道国的近2000个银行机构(包括各类分支机构)的数据研究了影响银行国际化区域分布的因素，发现贸易和直接投资以及东道金融发展是显著的影响因素。Dario和Alberto(2005)以OECD国家的260家大银行为对象探讨了影响银行对外投资的因素，发现国际化的区域选择和国家间的经济融合度相关，但东道国的制度和盈利机会的影响更大。Wezel(2004)以德国的银行为例，研究了影响银行国际化区域分布的因素，发现非金融FDI是最重要的影响因素，而东道国人均GDP以及贸易联系的影响也不可忽视。而George和Robert等人(2003)对银行国际化方面的文献进行了梳理，涉及银行国际化的动力(母国和东道国经济联系、东道国的机会、东道国的监管)、银行自身特点、国外银行的行动和对本地银行的影响等问题。近年来，中国这方面的研究包括：冯嗣全和欧阳令南(2004)从地理信息的角度研究了影响区域选择的众多因素，提出因素分等级加权的方法来选择目标区域。赵明铭和宋瑞敏(2009)也探讨了区位选择的影响因素，并对中国的银行国际区域分布情况进行了分析。江珲珲(2009)发现和东道国双边贸易、非金融FDI、自由贸易协定和东道国人均GDP等因素对于中国银行选择目标国有重要影响。类似的，孔庆洋(2010)探讨了东道国经济成长性，利润机会，金融市场状况，信息和制度方对区域选择影响。

然而，关于银行国际化区域选择的问题几乎全是影响因素的探讨，对于银行应如何从众多的备选国中选择最佳的目标国的讨论较少。在目标国选择的过程中，可以采用层次分析法，该方法在银行方面广泛应用，相关研究也较多。Rajshekhar等人(1989)研究了客户运用层次分析法来选择银行服务时，对于银行了解客户需求和偏好有何意义。与之类似，Huu和Kar(2000)运用层次分析法研究了新加坡大学生客户群体在选择银行方面的特点。Ami和Yair(1990)讨论了层次分析法在银行确定战略计划中的应用，并以兼并活动为例进行层次分析模型构建。如叶蓓(2007)和孟庆海(2009)分别研究了层次分析法在银行设立自助网点和营业网点选址中的应用(中文)。Ehsan(2009)以伊朗为例，运用层次分析法比较了四类电子银行业务在发展中国家发展程度情况。Nee等人(2009)应用层次分析法对土耳其银行业的总体经营表现进行了评价，指出财务表现和非财务表现均应受到重视。类似的，Hung等人(2009)对于多种反映银行表现的指标通过构造层次分析模型来探讨如何根据这些指标对银行给出综合评价。而Czeslaw and Jaroslaw(2005)则介绍了层次分析法在银行领域中的广泛用途。在中国的研究学者中，徐灼(2010)讨论了银行选址中应考虑的因素以及层次分析法的具体应用。田永强(2004)运用该方法分析了银行在贷款流向决策中如何做到最优化。而姜光磊和徐刚(2010)则讨论了金融危机爆发后银行在贷款流向决策的层次分析中准则层因素的新变化及其影响。刘晓欣和任建华(2010)论述了商业银行如何运用模糊层次分析法选择最合适的战略投资者。

目前，研究银行国际化区位选择以及层次分析法在银行业的应用两个主题的文献都较多，但是将两者结合起来，即运用层次分析法来研究银行国际化中应如何实现目标区域选择的最优化的研究还很少。本文将在这方面进行尝试。另外，层次分析法隐含地假设了决策者在了解影响因素和构建判断矩阵时均不会出错。这在纯数理上的研究是可行的，但是在实际的运用中却很难实现。因此，本文提出了带误差的层次分析法，分析了误差产生的原因及其对层次分析的影响，这也是本文重要创新。它不仅可以分析银行国际化区域选择的问题，而且也可以运用到其他各种层次分析法常涉及的问题中。

本文分为五部分，第二部分构建了银行国际化区域选择的层次分析基本模型；第三部分讨论准则层元素选择误差的影响；第四部分讨论了准则层元素相对重要性认定误差以及这些元素对应的判断矩阵设定误差的影响；第五部分为总结。

2.银行国际化区域选择的层次分析模型

2.1 区域选择的层次结构

层次分析法(Analytic Hierarchy Process，AHP)是一种分析多目标多准则的结合定性和定量分析的决策分析方法，是美国运筹学家T.L.Saaty提出的。这一方法对于难以完全定量分析的复杂系统的决策问题具独特优势，被广泛运用到军事、政治、工程和经济等领域以解决冲突求解、政策分析、项目优选、资源分配等问题。*层次分析法的基本原理可参见T.L.Saaty的相关论文，如How to make a decision：The analytic hierarchy process。也可参见由程理民等编著，清华大学出版社出版的《运筹学模型与方法教程》第246-256页，或者汪雷和宋向东主编，高等教育出版社出版的《线性代数及其应用》第175-179页。层次分析法在银行业务相关问题的应用主要集中在前文提到的贷款发放中客户的选择问题(贷款的分配)和银行网点的选址问题。当然银行业务中诸多涉及多目标多准则的决策中也可以运用这一方法。

对于银行国际化中的区位选择的层次分析(见图1)，假设判断的准则有n个，而备选的目标国有m个，则首先确定如下的层次结构：

2.2 准则层的确定

银行国际化过程中选择其目标区域的准则主要是影响其国际化经营活动的因素，每一重要因素都可以成为银行选择目标区域的准则之一。这些因素可从以下几个方面考虑：一是母国和东道国之间的经济关系；二是东道国总体经济情况；三是东道国的政策影响；四是东道国的微观影响因素。母国和东道国的经济联系用“经济一体化程度”反映；东道国总体经济情况的优劣决定了国际化银行的机遇，故用“市场机会”表示；东道国的政策影响主要指是否存在对外国银行的管制，如对业务开展、分支机构组织形式以及地区的限制等，这方面用“进入管制”表示；东道国的微观因素主要是外国银行进入后可能面临的当地银行的竞争，以及当地银行体系的发展程度，可用“东道国银行能力”表示。

银行进行国际化经营的最终目标是获取经济利益，如果东道国市场没有发展的潜力，未来盈利的可能性较低的话，银行国际化过程中较少考虑这样的东道国，因此市场机会是影响目标国选择的重要因素。经济一体化程度主要体现在双边贸易和非金融FDI、距离、文化和语言相似性、法律制度的相似性。经济一体化程度高既有客户跟随动机也有因为信息成本低、交易费用低而优先考虑这样的目标国。而且，双边贸易额和非金融FDI额度高也预示着双边对相互的国际金融服务的需求较高，国际银行业务具有一定的市场规模。然而进入管制可能使国际化银行无法有效地进入东道国的市场，即使该市场有良好的机会。因此，银行在进行国际化活动时必须考虑东道国的制度约束。在通常情况下，银行倾向于进入管制小的东道国开展业务，这将不会影响独立的决定，选择分支机构的组织形式以及开办的业务内容。最后，进入他国的市场需要和当地的银行竞争，如果东道国银行实力强劲，银行体系发展较完善，那么国外银行可能无法在竞争中获得优势进入这一的市场可能无法实现预期的目标。反之，进入银行体系发展不完善，进入东道国当地银行实力较弱的市场，国际银行将较容易发挥其比较优势。因此，以这四个方面的因素作为选择国际化经营的目标区域的准则层具有一定的合理性。这也得到了一些国内外研究的支持，除引言中提到的江珲珲(2009)、Wezel(2004)，以及Dario和Alberto(2005)的研究外，还有周天芸和王泽高(2009)以多个发展中国家为例研究了这些国家银行在海外设立机构的影响因素，发现东道国市场机会、金融发展水平和与母国相互贸易水平对于银行选择国际化目标国有显著影响。谢罗奇和何叔飞(2010)研究发现中国的银行国际化的影响因素中和东道国的贸易水平以及非金融FDI水平是两个重要因素。Douglas, Kang和Suresh(1986)发现美国在东道国的其他商业活动对美国在该国银行服务有正的影响，同时，东道国的开放程度(反映管制水平)也会影响美国银行国际化时的目标区域选择。Rigby和Young(2003)研究他国银行选择中国作为国际化经营的目标区域时发现文化和距离与亚洲的银行进入中国密切相关。

通过上述分析，设某银行在国家化过程中选择目标的区域时决策的准则层表示如下：C1表示经济一体化程度，C2表示东道国市场机会，C3表示东道国进入管制，C4表示东道国银行能力。同时为了表述方便用D1，D2，…，Dm表示方案层的备选目标国。

2.3 判断矩阵与排序结果

设根据准则层四个因素的相对重要性经过一致性检验并调整(下同)而得的目标层的判断矩阵为Oc，相应的准则层的判断矩阵为Cjd，j=1,2,3,4。具体设：

各矩阵设定的基本原则是保证对于经济一体化程度越高的目标国其重要程度的排序越高；对于市场机会越大的目标国其重要程度的排序高；对于进入管制多的目标国重要程度的排序低；对于东道国银行能力弱的目标国重要程度的排序高。

通过对以上判断矩阵求特征向量W，并经归一化处理，获得单排序权值。设判断矩阵Oc的经归一化处理的特征向量wo=(w01, w02, w03, w04)T。判断矩阵Cid的经归一化处理的特征向量分别为：

wc1=(wd11,wd12,…,wd1m)T；wc2=(wd21,wd22,…,wd2m)T；

wc3=(wd31,wd32,…,wd3m)T；wc4=(wd41,wd42,…,wd4m)T。

将Cid的各特征向量按顺序组成新的矩阵Os，即有：

设总排序向量为wT，则有

3.准则层确定误差的影响

从基本模型可以看出在层次分析的纯理论模型中，暗含着决策主体能够准确地确定全部影响因素的假设。进而准则层包括的元素是完备的，只要判断矩阵设定合理，则总排序向量的元素能够准确反映方案层各备选方案的优劣。然而，在实际应用中，某些情况下决策主体可能无法确定全部的影响因素，导致准则层的元素不完备。这将可能影响最后的判断。例如，本文涉及的银行国际地域选择问题，本身影响银行国际化成功的因素就很多，因此，一个银行在进行决策时，可能无法将全部影响其决策的因素考虑到。当然，如果是影响很小的因素，则不会对总排序的情况产出影响，这些因素可以忽略。但如果是某一或者某些重要因素未考虑，导致准则层中遗漏了相对重要的元素，则总排序可能引起决策失误。为说明这一种情况，以前一节的模型为基础，假设银行在层次分析时遗漏某一重要的因素Y(如风险因素)，该因素应被纳入准则层，并设其用C5表示。为简化分析，假设C5并不影响其他准则层元素两两间的相对重要性，而且银行在某一阶段或者某一次决策中仅从备选目标国中选择一个作为实施国际化经营的目标区域(下同)。显然，C5不影响其他四个准则对应的判断矩阵。因此，作为对比在引入C5后目标层对应的判断矩阵变为：

设矩阵Oc′的经归一化处理的特征向量wo′=(w01′,w02′,w03′,w04′,w05)T。

wo′=(w01′,w02′,w03′,w04′,w05)T=(w01L,w02L,w03L,w04L, 1-L)T。

设新的总排序向量为wT′，则有：

wTi′-wTi=wTiL+wd5i(1-L)-wTi=(wd5i-wTi)(1-L)

(1)

由(1)式可知两种情况下总排序向量对于元素值的变化受两个方面的影响：一是变化强度1-L，表示被遗漏因素在准则层的相对重要程度；二是变动方向wd5i-wTi。

当1-L趋近于0或者等于0时，表明遗漏的因素不重要，正如前文提到的，此时对总排序影响不显著，不会改变各备选目标国的排序。银行在进行决策时不考虑这些因素也不会导致决策失误。如果1-L显著异于0则将可能导致总排序发生显著变化，此时，若不考虑这些因素(如银行国际化中的各种风险)，则将可能导致选择目标国时出现失误。

当对于所有的i=1,2, …，m均有wd5i= wTi时，有wTi′= wTi，即考虑C5和不考虑C5总排序向量总的元素完全一样。而且此时，在进行层次分析将C1～C4作为准则层和仅将C5作为准则层的单因素决策其效果完全一致。*当C5作为单因素进行层次分析时，其总排序向量恰好就是wc5=( wd51, wd52,…,wd5m) T。因此，对于总排序而言，无论1-L的值如何，C5都是和准则层向量(C1，C2，C3，C4)以及(C1，C2，C3，C4，C5)完全等价。在进行决策时可以只依据某单一因素就可以做出和依据多因素一样有效的决策。在现实的决策中，这种情形出现的概率很小。稍符合实际情况的是在i=1,2, …，m中至少存在一个i使得wd5i和wTi不相等，进而某些wTi′和wTi也不相等。此时两种情况下的总排序对应的元素不是完全相等，而且和C5对应的经处理的特征向量对应的元素也不完全相等。但是，如果两个总排序向量和C5对应的经归一化处理的特征向量对应的元素的排序仍然一致的话，可以认为C5仍然和准则层向量(C1，C2，C3，C4)以及(C1，C2，C3，C4，C5)等价。虽然排序向量各元素值发生了变化但是排序不变的话，决策的结果通常是一致的。此时，单因素决策仍然有效。当两个总排序向量和C5对应的经处理的特征向量对应的元素均不相等，且排序也不相同，如果此时排序第一对应的备选方案始终是同一方案，则还是可以保证决策结果相同。可以认为C5依然和准则层向量(C1，C2，C3，C4)以及(C1，C2，C3，C4，C5)近似等价。

上述讨论说明了银行在进行国际化目标国选择时，有时采取简单的决策规则——单因素准则，为何能够作出正确的决策，也可以解释更一般的依据单因素决策任何可能获得良好效果的情形。然而，决策主体在事前可能无法判断应该依据哪一个单因素进行决策。这时依据单因素决策并获得成功的是基于概率上的巧合。因此，在实际的决策中，除非明确知道了等价的单因素，或者只有单一因素影响，否则决策主体还是倾向于考虑多因素的决策方式。

当两种情况下因C5而总排序向量各对应元素不是完全相等，且出现了排序的差异，导致两种情况下排位第一的目标国不一样，遗漏的决策因素会影响决策的合理性。此时设在原总排序向量中总排位第一的元素为wTf，则在wT中至少存在一个异于wTf的wTi满足：

(wd5i-wTi)(1-L)+wTi>(wd5f-wTf)(1-L)+wTf，

其中，wTi≠wTf因wTf>wTi，且L= K /(K+V5)，则不等式可表示为：

(2)

(2)式表示左边的分子是某个方案在C5判断矩阵的特征向量的对应元素与原最优方案在C5下的判断矩阵的特征向量对应的元素之差，分母是原总排序向量中两方案对应的元素之差。当其比值大于原目标层判断矩阵的特征向量各元素的和与C5在对应的新的目标层特征向量对应元素的值之比时，最终排序的变化会导致最优方案不同。当不存在满足(2)式的wTi时，遗漏因素可能会改变总排序向量某些元素的值，但不会影响排序第一的方案的排序位置。此时的C5是可忽略的因素。

4.判断矩阵依据客观标准对结果的影响

除可能遗漏重要的影响因素外，在基本模型中没有讨论判断矩阵获得方式的影响。在纯理论分析中，获得判断矩阵主要是决策主体根据自身的判断来确定各因素之间的相对重要性，带有较强的主观因素，尤其是当涉及个人的决策行为时。然而，在实际应用中，完全主观的决定各因素的相对重要性可能不合理，尤其当决策主体不是个人而是组织，如本文讨论到银行的时候。银行在国际化活动的决策中，其组织的决策往往是团队的决策，如银行国际业务部或者银行总部高层管理团队。在决策时，不能仅依靠主观的感觉来确定各因素之间的相对重要性，需同时有客观的数据、信息作为支撑。信息不完全可能导致对于各因素相对重要性认定失误，进而导致决策失误，而选定了非最佳的目标国。在讨论客观因素对判断矩阵的影响时，为简化分析，假设判断矩阵均是满足完全一致性的正互反矩阵。

在实际的决策中，银行不可能完全掌握需要的数据和信息，而且可能对于这些数据和信息的解读存在误差，导致对准则层因素相对重要性认定出现误差，进而得到的判断矩阵也和理想状态下存在差异。假设这使得实际的Oc的第一行元素为(1，c12+ε2，c13+ε3，c14+ε4)，ε表示误差。对于实际的特征向量此时有：V2=x/c12+ε2=x(c21+δ2)，V3=x/c13+ε3=x(c31+δ3)，V4=x/c14+ε4=x(c41+δ4)，其中δh=-εh/c1h(c1h+εh),h=2,3,4。δ为第一列各元素与理想状态的误差。可知(V1,V2,V3,V4)=(x，x(c21+δ2)，x(c31+δ3)，x(c41+δ4))T。经归一化处理后有：

则实际选择的目标国和理想状态下选择的不同。该不等式可简化为：

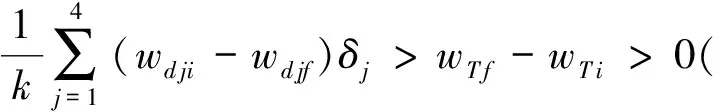
(3)

若不存在满足(3)式的wTi，则无论实际总排序向量和理想状态下的总排序向量有多大差异均能作出一样有效的决策，对于准则层各因素相对重要性认定的误差不会对最终决策的结果产生影响。

在讨论准则层各元素相对重要性认定误差时，假设了准则层各元素对应的判断矩阵是理想状态下的完全准确的反映备选目标国之间的相对关系。但在实际的银行决策中，在某一准则下对于备选目标国相对优劣关系(相对重要性)的认定也可能存在误差。除前文提到的数据和信息不完全，以及数据和信息的不正确解读外，还存在以下的原因导致银行在认定目标国行动优劣关系时出现误差。

首先，各备选目标国对于准则层的四个元素均是抽象的，很难量化处理。以C1经济一体化程度为例，母国和备选目标国的经济一体化程度的高低难以量化，因而不同备选目标国相对优劣关系难以确定。其次，每一个准则都由几个子因素构成(如果将这些子因素完全分开并明确地表现在次分析的结构中，则将大量增加准则层的元素或者会增加层次分析的层次数量，但仍不能消除误差。所以本文并没有将这些子因素表现在层次结构中，而是将它们归为四类)，而不同的备选目标国可能在这些子因素的构成方面是不同的，因而使得各备选目标国在认定准则层元素的相对优劣性比较时可能存在误差。因为经济一体化程度和双边贸易、距离、非金融FDI、文化和语言相似性、法律和制度相似性等因素相关，所以在比较某两个备选目标国时需要对这些子因素均作出比较。不同的目标国对银行来讲通常是不相同的，当某个目标国在其中某些子因素占优，而另一目标国在其他子因素占优时要比较两个国家总体上的C1的优劣可能会出现误差。所以在实际的决策中每个准则层元素对应的判断矩阵和理想状态下都可能存在差异。

在前文的基础上，设判断矩阵Cjd，j=1,2,3,4，是满足完全一致性的理想状态下的矩阵。因为每个判断矩阵中各元素的误差最终将反映在特征向量的差异上来，因此对于判断矩阵中各元素误差的讨论可以省略，而集中在特征向量差异的讨论。需说明的是，有可能存在某种特殊情况使得判断矩阵的各元素存在误差，但是特征向量的每个元素都不变，可看做误差被相互抵消或者等价于没有误差。假设判断矩阵中元素的误差导致特征向量中至少一个元素值发生变化，则总的排序向量就可能受到影响。具体的，假设实际的经归一化处理的准则层元素对应判断矩阵的特征向量为：wcr1=(wd11+δ11,wd12+δ12,…,wd1m+δ1m)T；wcr2=(wd21+δ21,wd22+δ22, …,wd2m+δ2m)T；wcr3=(wd31+δ31,wd32+δ32, …,wd3m+δ3m)T；wcr4=(wd41+δ41,wd42+δ42, …,wd4 m+δ4m)T。将实际的Cjd的各特征向量组成新的矩阵Osr有：

此时的实际总排序向量为：

可以看出理想状态和实际决策中的总排序向量的差异不仅受δ2，δ3和δ4的影响，还受δji的影响，总排序向量的差异将存在更多种情况，对这些情况分别讨论将更加复杂。因此，仍然从对决策产生实质影响的角度来分析。因m个备选的目标国在总排序向量中对应元素值的变化即使因为判断矩阵出现误差而出现多种情形，但只要最优备选的目标国前后一致则仍然不会影响实际决策的有效性。沿用前文的方法，设在理想状态下总排序向量中排位第一的元素为wTf，则在wT中如果至少存在一个异于wTf的wTi满足：

(4)

当不存在满足(4)式的wTi，则即使因为出现误差的判断矩阵增加了，实际总排序向量和理想状态下的总排序向量出现差异的可能性增加了，但这不会对最终决策产生影响。

当然，在通常情况下，出现误差的因素越多，误差越大对于决策有效性的影响越大，因此在实际的决策中要满足(4)式的可能性较小。可能银行实际的决策并不会实现理想状态下的最优。然而，一个理论上的困难是，我们知道每个银行在进行国际化决策时都有最贴合其当时情况的最佳选择(即理想状态下)存在，但是不能确定理想状态具体是什么。虽然有时在不知道理想状态的情况下仍能做出和理想状态一样有效的决策，但是这会降低我们在实施决策前的对其的信任度。当然，银行可以通过获得更多的信息和数据，并提高数据和信息分析能力来避免对判断矩阵设定的误差过大。如果这仍不能使得银行对于其决策满意，则在银行实际的决策中有两种方法来降低和理想状态的误差。一是在进行层次分析时，对备选目标国进行一个初步的筛选，这样即使因为出现误差而没有实现理想的最优决策，也可以保证一个相对正确的决策。二是在决策时对以往的国际化经营时目标区域选择的情况进行评估，总结已有的成功经验作为对新的决策中判断矩阵设定是否合理的参考。

误差层次分析看似对层次分析法的有效性提出了质疑，但在实际的应用中它在不影响层次分析法的优点的情况下反而可以增强层次分析法的有效性。因为当银行按照通常的层次分析法进行决策时，所有的人为因素或者客观因素导致的误差全都隐含在决策所依据的总排序向量中。这些误差在决策时没有被考虑到，但并不表示其不存在。而且正是因为没考虑到，这些误差不会被有意识地避免或者减少，所以导致决策的有效性受到影响。如果了解到层次分析中总会存在某些误差，并按前文所述方式有意识的避免或者减少误差，则存在误差的层次分析法反而使银行更能趋于最优的决策。

5.总结

本文讨论了层次分析法在银行国际化区域选择决策中的应用。为说明在银行进行层次分析时如何进行，根据现有研究的一些普遍共识以及银行国际化过程中实际影响因素的分析，在本文的基本模型中设定准则层的元素为经济一体化程度、东道国市场机会、东道国进入管制和东道国银行能力。通过基本模型的分析可看出层次分析法有助于银行国际化区域选择中做出正确的决策。然而，在银行实际在进行决策时，可能会出现各种误差。因此，本文提出并分析了存在误差的层次分析法。

误差包括两个方面：一是准则层遗漏重要因素；二是判断矩阵设定误差。在遗漏重要因素方面，如果银行决策时某些重要因素未考虑(如风险因素)，导致准则层遗漏了某些元素，则总排序将会不同。如果遗漏的因素重要程度较低，则将不会影响最优决策：若遗漏因素重要程度较高，则将导致目标国选择的非最优化。当遗漏的因素和已经考虑的因素等价或者近似时，最优决策也不受影响。特别是可能存在某些因素和某几个因素在决策时完全等价的情况，这为银行能依据单因素仍作出正确决策提供了一种解释。若遗漏重要因素导致总排序向量出现差异，则当些条件(本文为条件(2))被满足时会导致最终决策不同，条件不满足时最终决策保持一致。

判断矩阵设定误差方面。因为银行决策主体不是个人而是组织，在决策时，不能仅依靠主观的感觉来确定各因素之间的相对重要性，需要考虑客观因素。客观因素的存在导致银行可能设定和真实情况存在差异的判断矩阵，从而使总排序向量和理想状态存在差异。如果判断矩阵设定的误差导致总排序向量中排位最高的备选目标国和理想状态存在差异，则银行将不能做出最优决策；如果排位最高的备选目标国相同，则误差不会影响最优决策。

在实际决策中，当遗漏重要因素且所有的判断矩阵都可能存在误差时，银行可能不会实现理想状态下的最优。然而，带误差的层次分析法并不会影响银行在进行国际化经营的区域选择中的应用，相反会提高层次分析法的有效性。因为在银行不关注误差的情况下作出的决策，客观存在的误差不会被避免或者减少，决策有效性不高。但是，如果银行知道会存在误差并采取措施尽量避免或者减少误差，则层次分析法的结果将更可靠。从这个意义上讲，存在误差的层次分析法是在应用中对层次分析法的完善。为尽量降低这些误差银行可以通过获得更多的信息和数据，并提高数据和信息分析能力。银行还需要提高决策能力，在进行层次分析时，对备选目标国应先进行初步的筛选，并根据以往国际化经营时目标区域选择的情况进行评估，总结经验，准确认定各因素(备选目标国)的重要性(优劣)。

[1] 冯嗣全, 欧阳令南. 基于地理信息的银行国际化选址问题研究[J]. 财经论丛(浙江财经学院学报), 2004(1).

[2] 江珲珲. 中国商业银行国际化经营区位选择研究[D]. 南昌：江西财经大学, 2009.

[3] 孔庆洋. 商业银行国际化研究[D].上海：华东师范大学, 2010.

[4] 赵明铭, 宋瑞敏. 我国商业银行国际化发展的区位选择[J]. 对外经贸实务，2009(6).

[5] 赵迎迎. 高新技术型企业海外研发中心选址问题研究[J]. 中国市场, 2016(7).

[6] Alberto, F. P. Where do banks expand abroad? An empirical analysis[J].TheJournalofBusiness, 2005(78).

[7] Brealey, R. A., Kaplanis, E. C. The determination of foreign banking location[J].JournalofInternationalMoneyandFinance, 1996(15).

[8] Byeong, S. A. The analytic hierarchy process with interval preference statements[J].Omega, 2016(67).

[9] David, H. P. The Analytic Hierarchy Process in an uncertain environment: A simulation approach[J].EuropeanJournalofOperationalResearch, 1996(91).

[10] Ehsan, R. R. Evaluating electronic banking systems in developing nations through Analytic Hierarchy Process model: A case study[J].InternationalJournalofElectronicFinance, 2009(3).

[11] Fikri, D. F., Sharfuddin, A. K. Designing an integrated AHP based decision support system for supplier selection in automotive industry[J].ExpertSystemswithApplications, 2016(62).

[12] Hung, Y. W., Gwo, H. T. A fuzzy MCDM approach for evaluating banking performance based on Balanced Scorecard[J].ExpertSystemswithApplications, 2009(36).

[13] Huu, P. T., Kar, Y. H. A study of bank selection decision in Singapore using the analytical hierarchy process[J].InternationalJournalofBankMarketing, 2000(18).

[14] James, S. D. Remarks on the analytic hierarchy process[J].ManagementScience, 1990(36).

[15] Kang, R. C., Douglas, N. P. The role of location-related factors in US banking involvement abroad an empirical examination[J].JournalofInternationalBusinessStudies, 1986(17).

[16] Omkarprasad, S. V., Sushil, K.K. Analytic hierarchy process: An overview of applications[J].EuropeanJournalofOperationalResearch, 2006(169).

[17] Patrick, T. H., Luis, G. V. Reply to “remarks on the analytic hierarchy process” by J. S. Dyer[J].ManagementScience, 1990(36).

[18] Rajshekhar, G. J., Robert, L. A. Using the analytic hierarchy process for bank management: Analysis of consumer bank selection decisions[J].JournalofBusinessResearch, 1989(19).

[19] Thomas, L. S. A scaling method for priorities in hierarchical structures[J].Math.Psychology, 1977(15).

[20] Thomas, L. S. How to make a decision: The analytic hierarchy process[J].EuropeanJournalofOperationalResearch, 1990(48).

[21] Xiaoxin, L., Jianhua, R. Application of fuzzy analytical hierarchy process in the decision of strategic investors in commercial banks[J].ModernManagementScience,2010(5).

[22] Zhuo, X. On the AHP-based bank location[J].TheMerchandiseandQuality, 2010(5).

责任编辑：路小静

Analytic Hierarchy Process with Error and Foreign Banking Location

Diao Li1Deng Zhenxing2Hu Juan3

(1,2,3 Economics and Management School of Wuhan University,Wuhan, 430072)

This paper studies the application of AHP to the decision-making of internation-alization of bank location. When do so, the criteria level can include economic integration, opportunities in the host Country, regulation and bank capacity of the host Country. But the decision of a bank is made by a group of people and the judgment on the relative importance of the factors which affect foreign banking is according to objective factors. Thus there are many possibilities that cause missing important factor and setting a judgment matrix with error. When there is error in AHP, the lowest level of ranking vector will be different but the optimal decision will be the same if some conditions are satisfied. If not, the bank may not make an optimal decision. But the bank can decrease the errors and make the decision close to the optimal by enhance the ability of decision making and the skill of using AHP.

Analytic hierarchy process; Error; Foreign banking; Location

国家社科基金“一带一路相关国家贸易竞争与互补关系研究”(16ZDA039)。

刁莉，E-mail：fxyd39@126.com

F832.48

A