斯特林发动机配气活塞气体的作用效应

李 薇, 牟 健, 洪国同

(1.中国科学院理化技术研究所 北京，100190) (2．中国科学院大学 北京，100049)



斯特林发动机配气活塞气体的作用效应

李 薇1,2, 牟 健1,2, 洪国同1

(1.中国科学院理化技术研究所 北京，100190) (2．中国科学院大学 北京，100049)

为了能够深入认识自由活塞斯特林发动机配气活塞的运动特性，对动力活塞固定不动时的配气活塞的气体作用效应进行了分析，并设计了配气活塞的单独运动实验，在此基础上提出了配气活塞固有频率的计算式。分析了工作腔压力波超前与滞后配气活塞位移两种情况下受到的气体力的作用情况，采用旋转矢量法阐述了气体力的作用机理。当压力波超前或滞后活塞位移小于90°时，认为一部分气体力发挥了气体弹簧的作用，使系统固有频率增大；当压力波超前或滞后活塞位移大于90°但小于180°时，认为一部分气体力发挥了惯性力的作用，使系统固有频率减小。热源温度越高，系统的固有频率越小。利用本实验室的一台自由活塞斯特林发动机进行实验，验证了上述气体力作用的效应与规律，且利用此理论计算了系统固有频率的准确性。

斯特林发动机； 自由活塞； 配气活塞； 气体作用效应； 固有频率

引 言

随着空间技术的发展，进入21世纪后，美国、俄罗斯、日本以及欧洲的主要航天大国纷纷提出了一系列深空探测的任务计划，而这些计划的实施也对空间电源提出了新的要求[1-3]。利用斯特林循环将热能转化为电能的自由活塞斯特林发电机，因其具有热电转化效率高、质量轻及体积小等优点，越来越受到航天大国们的重视，纷纷开展相关研究[4-7]。

自由活塞斯特林发动机是斯特林发动机的一种结构形式，其动力活塞和配气活塞运动没有机械结构的限制，因而被称为“自由活塞”[8]。自由活塞斯特林发动机不仅具有传统斯特林发动机理论效率高、外燃型等优点，还因为取消了传统斯特林发动机的曲轴连杆结构，具有噪声和振动小、寿命长等优点[9]。

对于自由活塞斯特林发动机而言，如果简单地对发动机整机进行系统实验，只能测试到整机的系统热力学和动力学参数，而忽略了各部件的动力学特性及其相互之间的影响规律，相关的特性信息会被丢失，很难深入研究发动机的内在动力学特性、耦合过程及其对启动运行的影响规律。笔者在对配气活塞单独进行动力学特性实验研究的过程中，发现系统的固有频率会随着热源温度的升高而降低。由于固有频率对改善系统稳定性和快速响应性起到至关重要的作用，长期以来一直被各行业作为研究的热点问题[10-11]。对于自由活塞斯特林发动机而言，配气活塞的固有频率对整机的运行频率起到关键性作用。针对这个问题，对配气活塞振动系统的固有频率进行了较深入的理论与实验研究。

1 配气活塞振动系统的动力学模型

配气活塞单独动力学实验装置由气缸、配气活塞、动力活塞、加热器、回热器、冷却器和配气活塞驱动电机等组成,具体结构如图1所示。配气活塞上端为热腔，通过高温换热器与热源(加热棒)交换热量。配气活塞下端为冷腔，通过冷却器向外界散热。热腔和冷腔之间通过回热器连接，回热器为环状，位于配气气缸的外侧，与其同轴。冷腔下端是动力活塞，动力活塞固定在实验装置缸体上，处于轴向某个位置，保持不动。动力活塞下端是缓冲腔，配气活塞的驱动电机固定在缓冲腔内，通过配气活塞杆(从动力活塞中间穿过)与配气活塞相连。

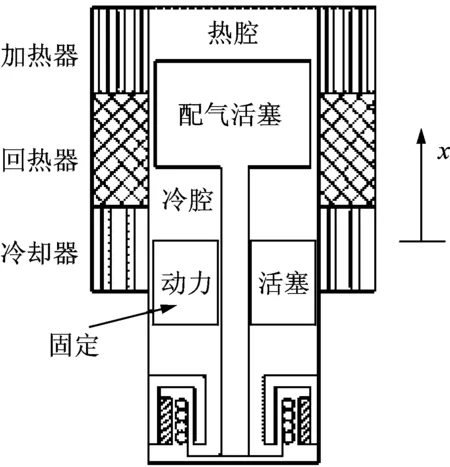
图1 实验装置结构示意图Fig.1 Schematic diagram of experimentalapparatus

自由活塞斯特林发动机配气活塞的动力学模型可以用机械振动系统来诠释，其受力分析如图2所示。运动方程为

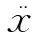
(1)

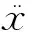
从式(1)可以看出，由于气体力的出现，配气活塞的运动方程不再是标准的阻尼受迫振动方程，配气活塞的刚度也不再是单纯的机械板弹簧刚度，气体力在一定程度上表现出阻尼、弹簧与惯性的作用而影响配气活塞的运动。所以，如何确定气体力的作用效应就成为计算配气活塞固有频率的关键。

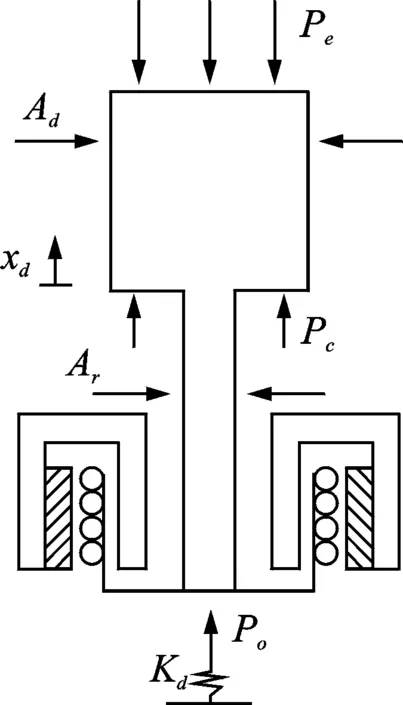
图2 配气活塞的受力示意图Fig.2 Force diagram of displacer

由图2可知，配气活塞的气体驱动力为

(2)

其中：Pe为热腔压力；Pc为冷腔压力；Po为缓冲腔压力；Ad为配气活塞面积；Ar为配气活塞杆面积；Ap为动力活塞面积(其中Ap=Ad-Ar)。

特殊地，当热腔和冷腔的压力相等时

Fd=(Ad-Ap)ΔP=ArΔP

(3)

从配气活塞气体驱动力的表达式可以看出，气体驱动力与各个腔体的压力、配气活塞面积及配气活塞杆的面积有关。当配气活塞的结构参数一定时，各个腔体的压力就决定了气体驱动力的大小和方向。由于斯特林发动机在高低温热源间工作，工作腔内的压力变化不仅与工作腔的体积变化有关，同时受到冷热源温度的影响。随着冷热腔温度的变换，压力波幅值和相位也会发生改变，气体力对配气活塞的作用效果也不同。下面就压力波超前和滞后活塞位移两种情况下的气体压力对配气活塞的作用效应进行分析。

2 压力波超前位移时的气体作用效应

2.1 超前角度α≤90°

热腔与冷腔压力波超前配气活塞位移角度小于90°时的气体力的矢量图如图3所示。规定横坐标为位移，并且横坐标向左的方向为位移正方向。由于两腔体的压力波都超前活塞位移，且小于90°，所以冷腔的气体作用力位于矢量图的第三象限中。由于热腔的压力Pe对活塞的作用力与规定正方向的方向相反，所以转动180°，位于矢量图的第一象限中。配气活塞最终受到的气体作用力是两腔体气体力的合力。由图3可知，热腔的气体作用力与冷腔的气体作用力方向相反，所以合力的大小为两腔体作用力的差值，正方向与热腔气体力的方向相同。

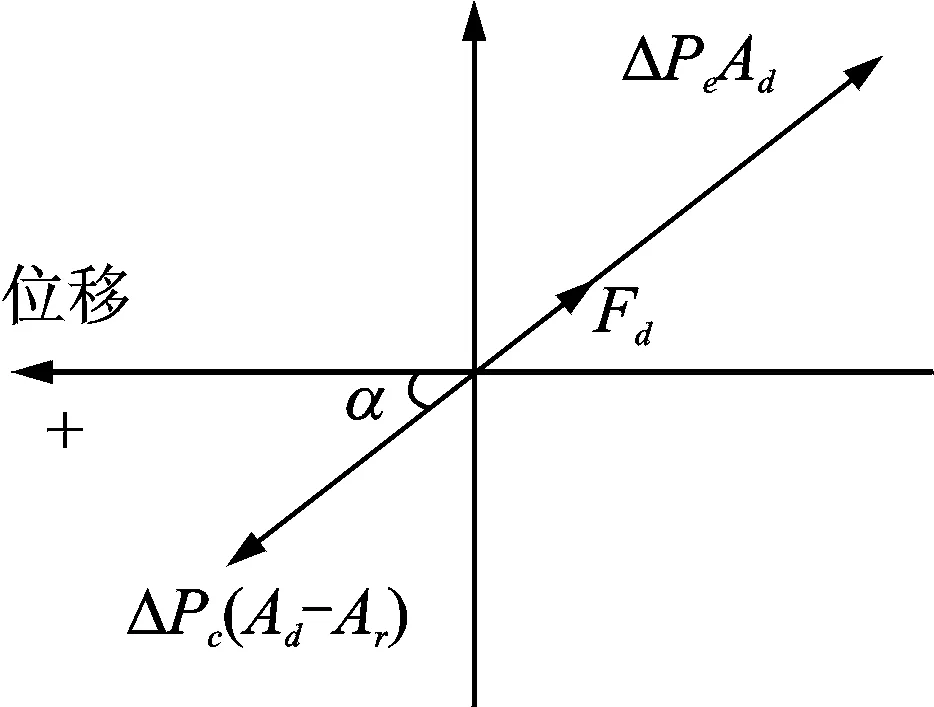
图3 气体力矢量图(超前α≤90°)Fig.3 Vector diagram of gas force ( leading α≤90°)

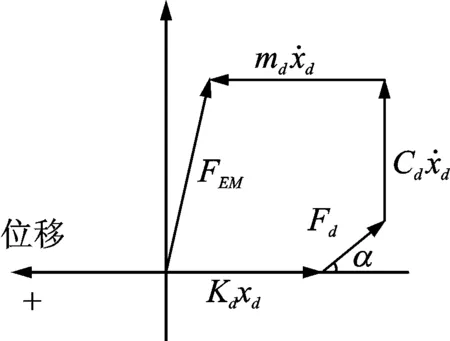
图4 活塞受力的旋转矢量图(超前α≤90°)Fig.4 Rotation vector diagram of force on the displacer(leading α≤90°)

从图4可知，气体力可以分解为两个力，一个是垂直于位移方向的气体阻尼力，一个是平行于位移方向的气体弹簧力。在特殊情况下，当α=0时，两腔体的气体力与横坐标平行，合力全部起到气体弹簧力的作用；当α=90°时，两腔体的气体力与横坐标垂直，合力全部起到气体阻尼力的作用。在热腔与冷腔压力波超前活塞位移角度小于90°的情况下，气体阻尼的数值为

(4)

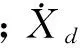
对于弹簧力而言，该情况可以认为机械板弹簧与气体弹簧并联，系统的总弹簧刚度等于板弹簧的弹簧刚度与气体弹簧刚度相加。配气活塞的固有频率为

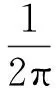
(5)

系统的总弹簧刚度为

k=(kdXd+Fdcosα)/Xd

(6)

气体弹簧刚度为

kg=k-kd=Fdcosα/Xd

(7)

其中：Xd为配气活塞位移的振幅。

2.2 超前角度90°<α≤180°

图5为热腔与冷腔压力波超前配气活塞位移角度大于90°但小于180°时的气体力矢量图，图中依然规定横坐标为位移，并且横坐标向左的方向为位移正方向。由于两腔体的压力波都超前活塞位移，且大于90°，所以冷腔的气体作用力位于矢量图的第四象限中。由于热腔的压力Pe对活塞的作用力与规定正方向的方向相反，所以转动180°，位于矢量图的第二象限中。配气活塞最终受到的气体作用力大小同样为两腔体作用力的差值，正方向与热腔气体力的方向相同。

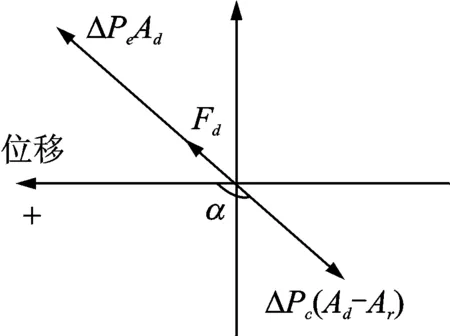
图5 气体力矢量图(超前90°≤α≤180°)Fig.5 Vector diagram of gas force(leading 90°≤α≤180°)

图6给出了热腔与冷腔压力波超前活塞位移角度大于90°但小于180°时的旋转矢量图。从图6可知，气体力同样可以分解为两个力，一个是垂直于位移方向的气体阻尼力，一个是平行于位移方向的气体惯性力。在计算配气活塞的固有频率时，需要将系统的动质量与气体惯性力中的质量相加。特殊情况下，当α=90°时，两腔体的气体力与横坐标垂直，合力全部起到气体阻尼力的作用；当α=180°时，两腔体的气体力与横坐标平行，合力全部起到气体惯性力的作用。

此时，配气活塞的气体阻尼和固有频率仍然分别由式(4)和式(5)计算，系统的弹簧刚度仅为机械弹簧刚度，系统的总质量为

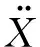
(8)

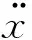
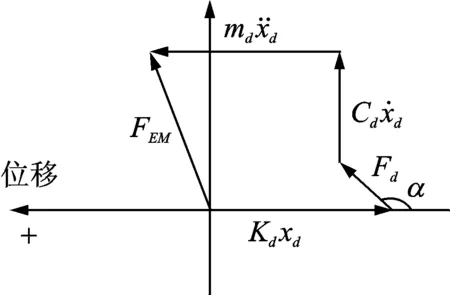
图6 活塞受力的旋转矢量图(超前90°≤α≤180°)Fig.6 Rotation vector diagram of force on the displacer(leading 90°≤α≤180°)

3 压力波滞后位移时的气体作用效应

3.1 滞后角度α≤90°

热腔与冷腔压力波滞后活塞位移小于90°时的矢量图如图7所示。由于两腔体的压力波滞后活塞位移小于90°，所以冷腔的气体作用力位于矢量图的第二象限中。热腔的压力Pe对活塞的作用力与规定正方向的方向相反，位于矢量图的第四象限中。配气活塞最终受到的气体作用力大小同样为两腔体作用力的差值，正方向与热腔气体力的方向相同。

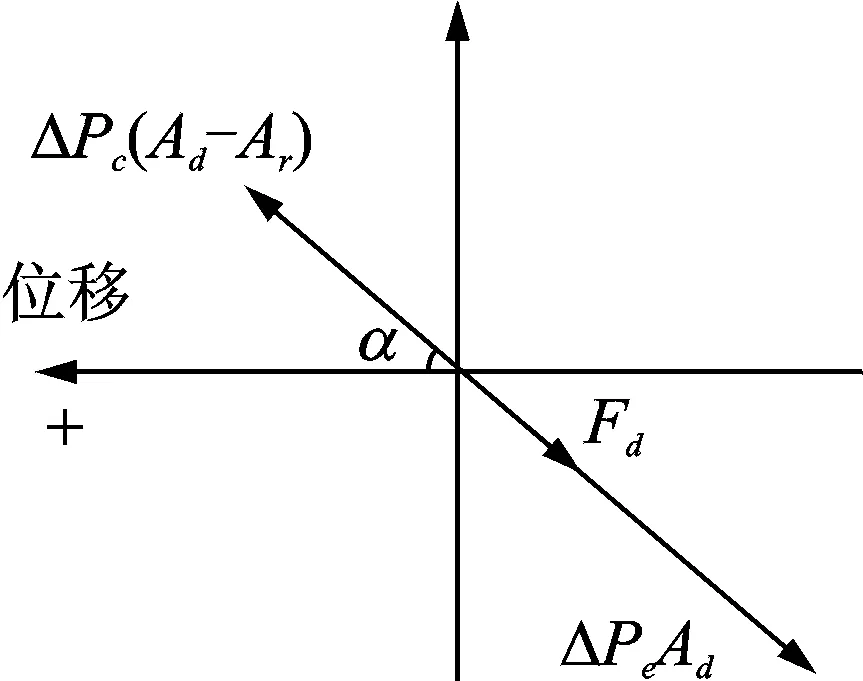
图7 气体力矢量图(滞后α≤90°)Fig.7 Vector diagram of gas force ( lagging α≤90°)

图8给出了热腔与冷腔压力波滞后活塞位移角度小于90°时的旋转矢量图。当其他参数不变时，气体力分解为两个力：a.垂直于位移方向、且与阻尼力方向相反的力；b.平行于位移方向的气体弹簧力，气体弹簧与机械弹簧并联。此时，配气活塞的气体阻尼和固有频率分别由式(4)和式(5)计算，系统总的弹簧刚度和气体弹簧刚度分别采用式(6)和式(7)计算。

特殊情况下，当α=0时，两腔体的气体力与横坐标平行，合力全部起到气体弹簧力的作用；当α=90°时，两腔体的气体力与横坐标垂直，合力全部起到抵制气体阻尼力的作用。

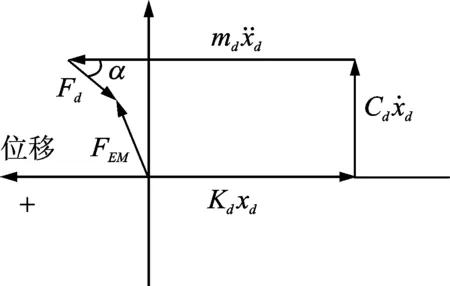
图8 活塞受力的旋转矢量图(滞后α≤90°)Fig.8 Rotation vector diagram of force on the displacer(laggingα≤90°)

3.2 滞后角度90°<α≤180°

热腔与冷腔压力波滞后活塞位移角度大于90°但小于180°时的气体矢量图如图9所示。由于两腔体的压力波滞后活塞位移，且均大于90°，所以冷腔的气体作用力位于矢量图的第一象限中。热腔的压力Pe对活塞的作用力与规定正方向的方向相反，位于矢量图的第三象限中。配气活塞最终受到的气体作用力大小同样为两腔体作用力的差值，正方向与热腔气体力的方向相同。

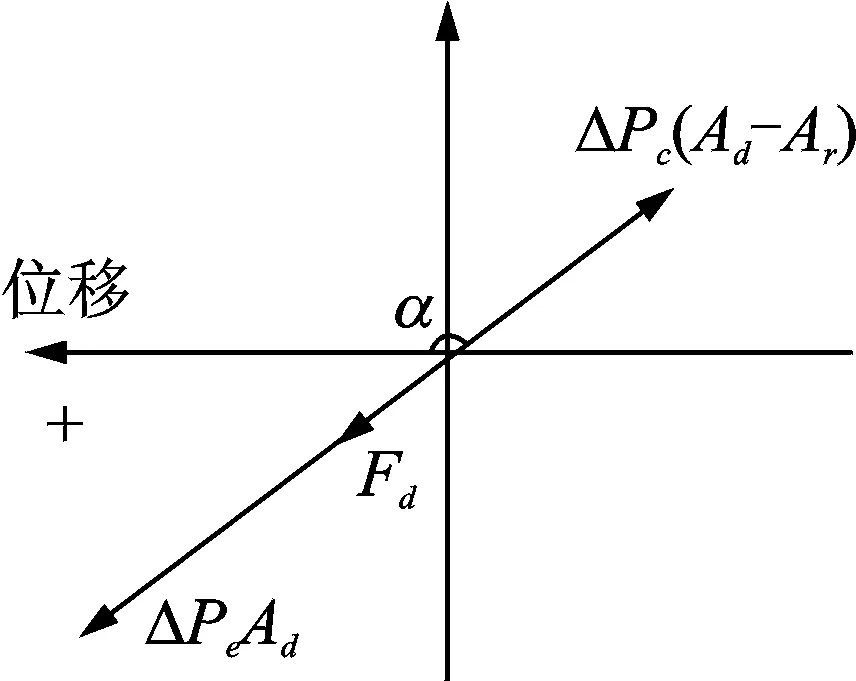
图9 气体力矢量图(滞后90°≤α≤180°)Fig.9 Vector diagram of gas force (lagging 90°≤α≤180°)

图10给出了热腔与冷腔压力波滞后活塞位移角度大于90°但小于180°时的旋转矢量图。当其他参数不变时，气体力同样分解为两个力：a.垂直于位移方向、且与阻尼方向相反的力；b.平行于位移方向的气体惯性力。此时，配气活塞的气体阻尼和固有频率由式(4)和式(5)计算，系统的弹簧刚度仅为机械弹簧刚度，系统总质量包括气体等效动质量，计算式为式(8)。

特殊情况下，当α=90°时，两腔体的气体力与横坐标垂直，合力全部起到抵制气体阻尼力的作用；当α=180°时，两腔体的气体力与横坐标平行，合力全部起到气体惯性力的作用。

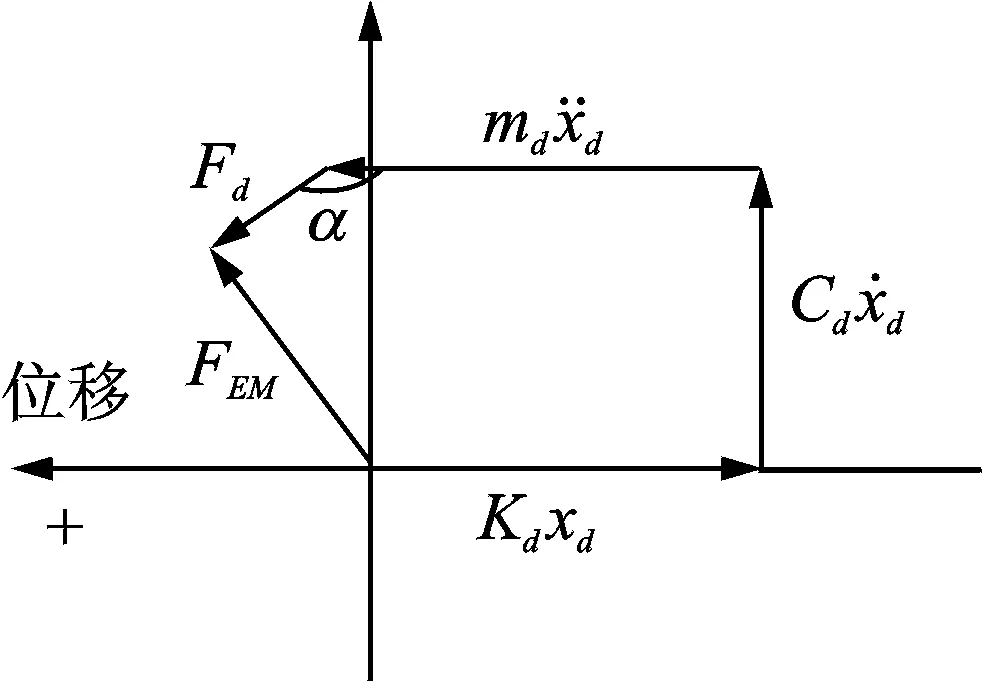
图10 活塞受力的旋转矢量图(滞后90°≤α≤180°)Fig.10 Rotation vector diagram of force on the displacer(lagging 90°≤α≤180°)

4 实验结果及分析

该实验是在一台输出100W的自由活塞斯特林发动机上进行，实验装置通过位移传感器和压力传感器获得配气活塞位移和冷热腔压力的实验数据。将这些实验数据代入式(2),(4),(6),(7),(8)及式(5)，计算得到气体力、气体阻尼系数、系统总的弹簧刚度、气体弹簧刚度、系统总质量和系统固有频率。同时采用共振法对系统进行实验测得其系统的实际固有频率，比较两种固有频率的大小以验证上述气体力作用效应理论的正确性。

实验装置的配气活塞组件的运动质量为327g，板弹簧刚度为4 300N/m，充气压力为2MPa时，配气活塞位移和冷热腔压力在不加热与加热两种情况下的运行参数如表1所示。从表1可以看出，系统内不加入热源时，冷热腔体的压力波幅值较小，且两腔体的压力波均超前活塞位移约20°；系统内加入热源时，随着热源温度的升高，冷热腔的压力波幅值逐渐增大，两腔体的压力波滞后活塞位移约150°。图11给出了配气活塞位移和冷热腔压力在不加热与热源温度为500℃时的实验曲线图。

表1 不同热源温度下的运行参数

Tab．1 Operational parameters in different temperatures

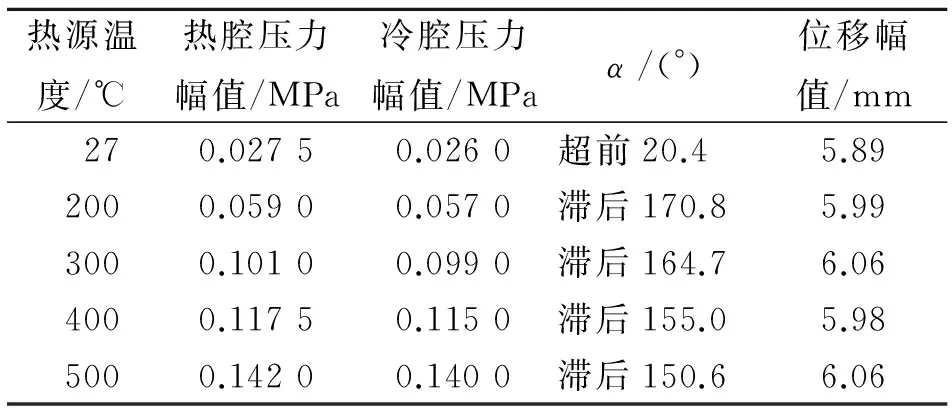
热源温度/℃热腔压力幅值/MPa冷腔压力幅值/MPaα/(°)位移幅值/mm270.02750.0260超前20.45.892000.05900.0570滞后170.85.993000.10100.0990滞后164.76.064000.11750.1150滞后155.05.985000.14200.1400滞后150.66.06

表2给出了不同热源温度时系统的机械阻尼、气体阻尼和总阻尼系数。系统的机械阻尼是实验装置在真空条件下，采用激振的方法，得到活塞自由振动的衰减曲线，计算阻尼率，从而计算出活塞运动阻尼系数。气体阻尼是由式(4)计算得到的。总阻尼是在不同热源温度下，利用激振法计算得到的。由表2可知，机械阻尼与气体阻尼相加的数值要小于测得的总阻尼。同时，热源温度越高，气体阻尼占总阻尼的比例越大，对总阻尼的影响也越大。

表2 不同热源温度下系统的阻尼值

Tab．2 Damping value under different temperatures of heat source

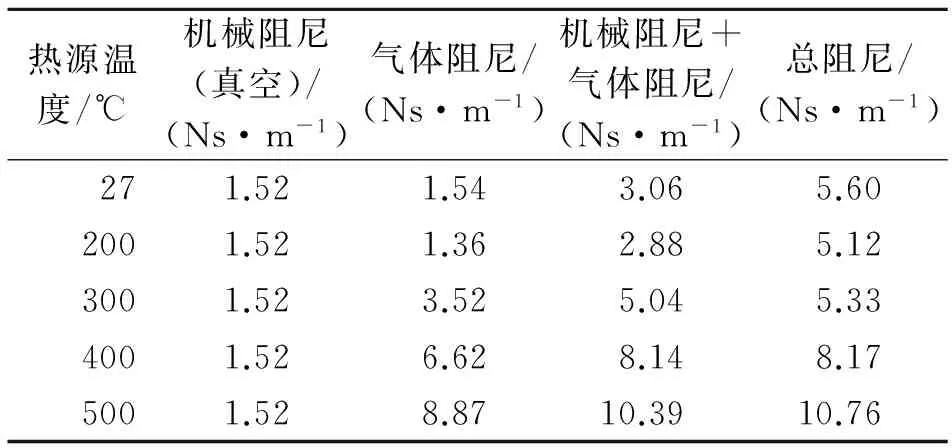
热源温度/℃机械阻尼(真空)/(Ns·m-1)气体阻尼/(Ns·m-1)机械阻尼+气体阻尼/(Ns·m-1)总阻尼/(Ns·m-1)271.521.543.065.602001.521.362.885.123001.523.525.045.334001.526.628.148.175001.528.8710.3910.76

表3不仅给出了系统刚度和固有频率的计算结果，还根据阻尼固有频率的计算表达式

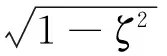
(9)

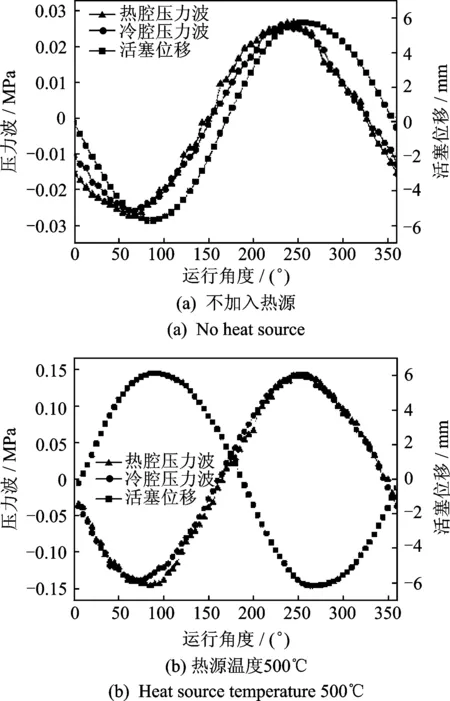
图11 活塞位移和冷热腔压力在不加热与加热两种情况下的实验曲线Fig.11 Experimental data of displacement and pressure with and without heat sources

给出了不同热源温度下阻尼固有频率的计算结果。从计算值可以看出，室温下，由于压力波超前位移处于0～90°之间，此时，气体表现出气体弹簧刚度特性，系统总的弹簧刚度增加，固有频率比无气体时的配气活塞运动系统的大；随着热源温度的升高，压力波滞后活塞位移处于90°～180°之间，气体表现出等效动质量特性，使得系统总的运动质量增加，整个系统的弹簧刚度和固有频率逐渐减小，系统阻尼固有频率变化不大，对整个振动系统的固有频率几乎没有影响。

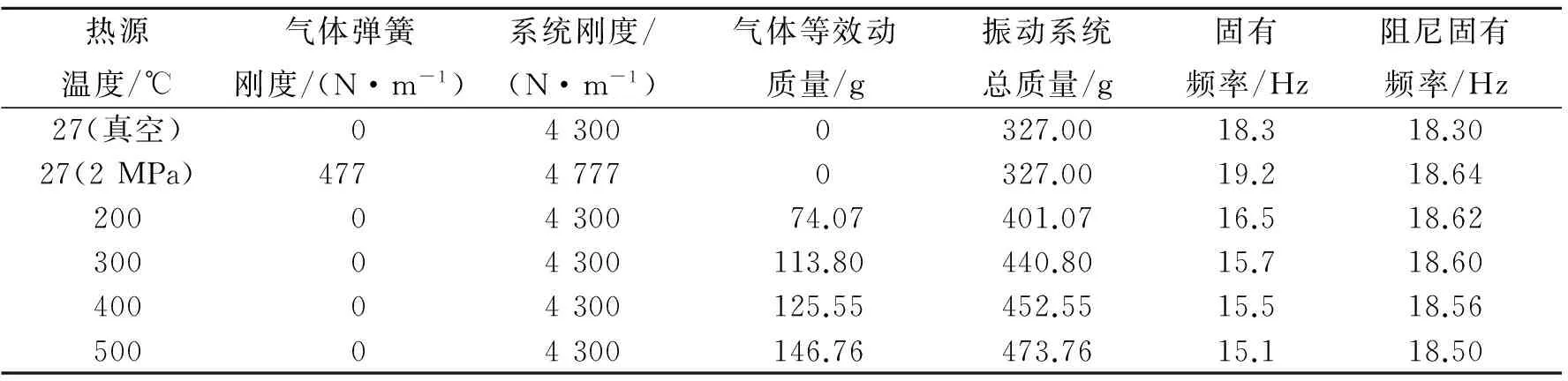
表3 不同热源温度下系统刚度和共振频率的计算值

为了验证上述理论的正确性，采用共振法对系统的固有频率进行实际测量。测量时，保持电机驱动功率不变，只改变频率，测量不同频率下活塞的位移，位移最大时对应的频率即为固有频率。实验测得不同加热温度下系统的固有频率见表4。从表4可以看出，随着热源温度的升高，系统固有频率减小。

表4 不同热源温度下系统共振频率的实验值

Tab．4 Experimental values of the system resonance frequency under different temperatures heat source

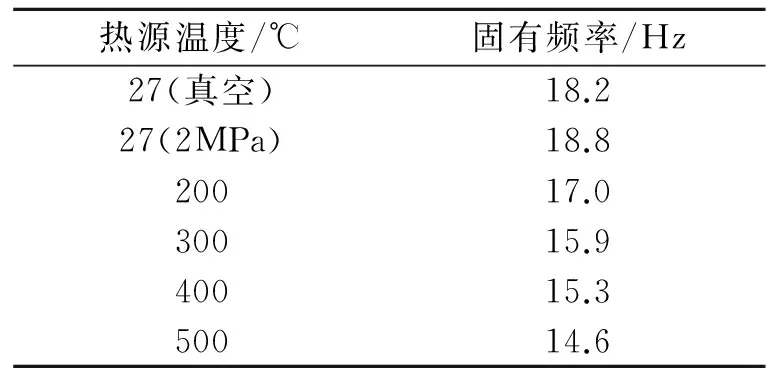
热源温度/℃固有频率/Hz27(真空)18.227(2MPa)18.820017.030015.940015.350014.6

将表3中固有频率的计算值与表4中的实测值进行对比，可以发现计算值与实测值非常吻合，最大误差仅为0.5 Hz,从而证明了所提出的固有频率计算方法的正确性，也证明了配气活塞存在明显的气体弹簧和气体动质量作用效应，这种效应随热腔工作温度的升高或冷热源温度差的增加而增大。

5 结 论

1) 当系统热腔与冷腔压力波超前或滞后配气活塞位移角度α≤90°时，一部分气体力起到了弹簧力的作用，系统总的弹簧刚度等于机械弹簧力与气体弹簧力之和与位移的比值，此时认为气体弹簧与机械弹簧并联，系统总的弹簧力增大。

2) 当系统热腔与冷腔压力波超前或滞后活塞位移角度90°<α≤180°时，一部分气体力起到了惯性力的作用，系统总的质量等于机械动质量与气体等效动质量之和，系统总的惯性力增大。

3) 当系统热腔与冷腔压力波超前配气活塞位移时，一部分气体力表现为气体阻尼作用，使得系统总的阻尼增大；当系统热腔与冷腔压力波滞后配气活塞位移时，一部分气体力则表现为气体负阻尼作用，使得系统总的阻尼减小。

4) 对于自由活塞斯特林发动机而言，随着热源温度的升高，压力波滞后位移角度减少，气体阻尼逐渐增大，气体等效动质量也增大，系统固有频率降低。

[1] Worms J C, Haerendel G. The european white paper on space: enough support for basic science?[J]. Space Policy, 2004, 20(2): 73-77.

[2] Zhou Yi. Perspectives on Sino-US cooperation in civil space programs[J]. Space Policy,2008,24(3):132-139. [3] Bignami G F. European vision for space science[J]. Space Research Today, 2005, 164: 8-15.

[4] Schock A, Or C, Kumar V. Radioisotope power system based on improved derivative of existing stirling engine and alternator[C]∥30th Intersociety Energy Conversion Engineering Conference. Orlando,FL,United States:[s.n.],1995．

[5] Or C, Kumar V, Carpenter R, et al. Self-supporting radioisotope generators with STC-55W stirling converters[J]. AIP Conference Proceedings,2000, 504(1): 1242-1251.

[6] Or C, Carpenter R, Schock A, et al. Performance of the preferred self-supporting radioisotope power system with STC 55-W stirling converters[J].AIP Conference Proceedings,2000, 504(1): 1252-1259.

[7] Cockfield R D. Radioisotope power system options for future planetary missions[J].AIP Conference Proceedings, 2001, 552(1): 740-746.

[8] G. 沃克.斯特林发动机[M]. 朱炜青，钱国柱，韩如，等译.北京:机械工业出版社, 1987:2-3.

[9] 钱国柱. 热气机设计[M]. 北京：国防出版社，1987:7-19.

[10]上官文斌，陈超，段小成，等.发动机曲轴系统扭转振动建模与实测分析[J].振动、测试与诊断,2012, 32(4):560-567.

Shangguan Wenbin,Chen Chao, Duan Xiaocheng, et al. Modeling and experimental analysis of torsional vibration in engine crankshaft syatem[J]. Journal of Vibration, Measurement& Diagnosis, 2012,32(4)：560-567.(in Chinese)

[11]王俨剀，马进锐, 廖明夫，等.发动机振动趋势预测模型研究[J].振动、测试与诊断，2014,34(3):516-523.

Wang Yankai, Ma Jinrui, Liao Mingfu, et al.Research on trend prediction model of engine vibration[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(3)：516-523.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.03.023

2015-03-19；

2015-05-16

TH113.1； TK441+.1

李薇，女，1984年2月生，博士生。主要研究方向为自由活塞斯特林发动机动力学。曾发表《自由活塞斯特林发动机的间隙密封泄漏特性分析》(《真空与低温》2012年第18卷第2期)等论文。 E-mail:liweitipc@163.com