基于KPCA和WPHM的滚动轴承可靠性评估与寿命预测

王奉涛， 陈旭涛， 柳晨曦， 李宏坤， 韩清凯， 朱 泓

(大连理工大学机械工程学院 大连， 116024)



基于KPCA和WPHM的滚动轴承可靠性评估与寿命预测

王奉涛， 陈旭涛， 柳晨曦， 李宏坤， 韩清凯， 朱 泓

(大连理工大学机械工程学院 大连， 116024)

为了评估滚动轴承的可靠性和预测剩余使用寿命，选取能够反映性能退化过程的特征参数作为寿命预测模型的输入参数，提出一种基于核主元分析(kernel principal component analysis，简称KPCA)和威布尔比例故障率模型(Weibull proportional hazards model, 简称WPHM)的方法。首先，提取滚动轴承全寿命周期的时域、频域及时频域等多特征参数，从中筛选出有效的特征参数，构建高维相对特征集；其次，进行核主元分析，选取能够反映轴承全寿命周期性能退化过程的核主元，进而作为WPHM的协变量来进行可靠性评估和剩余寿命预测。通过滚动轴承全寿命试验，验证了该方法能够对轴承进行准确的可靠性评估和剩余寿命预测，以提供及时的维修决策。同时，由于提取的是相对特征，降低了同种轴承间在制造、安装及工况的差异，增强了该方法的适用性和稳定性。

滚动轴承；寿命预测；核主元分析；威布尔比例故障率模型；相对特征

引 言

滚动轴承是旋转机械的关键组成部件之一，其性能的好坏直接影响整台机器能否正常运转。在滚动轴承发生损毁之前，对轴承进行主动维修保养可以有效避免恶性事故的发生，最大程度地减少生命财产损失[1]。有效的维修策略不仅可以减少停机次数和降低维修成本，而且可以保障整个设备的正常运行[2-3]。若要根据设备的实时状态做出正确的维修决策，准确寿命预测所提供的依据不可或缺。

对设备进行准确的寿命预测主要面临两个关键问题：a.建立合适的寿命预测模型；b.选取能够准确反映性能退化过程的特征参数作为模型输入参数。随着信息新技术的发展，基于状态监测的轴承寿命预测方法成为国内外研究的热点[4]。其中比例故障率模型(proportional hazards model, 简称PHM)[5]是一种适用性很强的寿命数据统计分析方法。它对数据分布、残差分布均无特殊要求，且可以对截尾数据进行分析，属于一种根据设备状态监测和历史寿命等数据信息建立失效模型的建模方法，在设备寿命预测领域有强大的发展。丁峰等[6]将基于设备振动信号的均方根值(root mean square, 简称RMS)和峭度作为协变量，利用布尔比例故障模型(Weibull proportional hazards,简称WPHM)实现了对铁路机车轮滚动轴承的可靠性评估。Zhang等[7]基于依赖分析和比例故障率模型，对固体润滑轴承建立有效的加速寿命试验模型。Zhang等[8]通过混合威布尔比例故障率模型，来预测含有多个失效形式的机械系统的剩余使用寿命(remaining useful life, 简称RUL)。

以往的研究大多是针对运行状态信息直接进行时域统计分析，然后从中选择一个或多个时域特征建模。然而单个特征或单域特征存在评估能力不足的问题，无法准确表征轴承性能退化全周期过程，严重影响可靠性评估和寿命预测的准确性。而时域、频域、时频域等多域特征虽然能够综合地表征全周期轴承的性能退化过程，但特征过多时存在冗余性，而WPHM的协变量越多，模型的参数估计越困难，因此直接代入多域特征作为WPHM协变量进行寿命预测不太现实。因此，有效剔除对反映故障特性贡献不大、甚至不敏感的特征，并降低特征间的相关性，减少信息冗余，选取准确表征轴承性能退化过程的特征作为协变量对轴承寿命预测至关重要。

主元分析(principal component analysis, 简称PCA)，作为一种线性降维方法，广泛应用于提取特征集的主要信息，但复杂工况下故障机械的振动信号是非平稳和非线性的[9]。Scholkopf等[10]提出的KPCA作为一种非线性分析方法，通过非线性映射将原始数据投影到一个特征空间，然后进行主元分析，从而得到具有更好可分性的非线性主元[11]，该方法目前已在过程监控和故障诊断中得到越来越多的关注和成功的应用。李巍华等[12]提出基于核函数主元分析的齿轮故障诊断方法，将非线性主元作为特征子空间对齿轮工作状态进行分类识别。Lee等[13]基于KPCA提出了一种新的非线性过程监测技术。He等[14]从测量信号的统计特征中提取低维主元来表征和监测齿轮箱的状态。

针对WPHM在选取协变量方面的不足，笔者选取降维后能充分表征轴承性能退化全周期过程的前3个核主元作为WPHM的协变量，来进行可靠性评估和剩余寿命预测。通过滚动轴承全寿命试验，验证了该方法能够对滚动轴承进行准确的可靠度评估和剩余寿命预测，为设备主动维修提供重要的依据。由于提取的是相对特征，降低了同种轴承间在制造、安装及工况的差异，增强了该方法的适用性和稳定性。

1 理论基础

1.1 核主元分析

KPCA的基本思想是利用映射函数将原始数据空间投影到特征空间，再进行线性运算。具体算法如下。

(1)

2) 矩阵ST对应的特征方程为

λV=STV

(2)

其中：λ为特征值；V为特征向量。

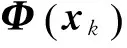
(3)

(4)

其中：aj为相关系数。

将式(4)代入式(3)得

(5)

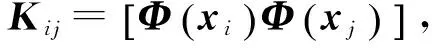
由特征向量a求出ST的特征向量V，得到映射空间F的主元方向。对K对角化，λ1≥λ2≥…≥λp≥…≥λN表示K的特征值，a1,a2,…,ap,…,aN为对应的特征向量。设λp为大于零的最小特征值，对特征向量进行归一化，令

(6)

5) 计算m个测试样本在特征空间中前p个轴的投影为

(7)

其中

对映射数据进行中心化，相应K变为

(8)

其中：lN为系数为1/N的N×N阶单位矩阵。

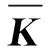
定义累计贡献

(9)

其中：p为输入向量空间维数；ηp为前p个核主元的累计贡献率。

1.2WPHM模型

PHM建立了设备运行状态特征与可靠度之间的数学关系，根据当前实时运行状态特征，得到当前状态的故障率。采用基底函数为威布尔分布的PHM为WPHM，其故障率函数为

(10)

其中：β>0为威布尔分布形状参数；η>0为威布尔分布尺度参数。

可靠性函数和概率密度函数分别为

(11)

(12)

极大似然估计广泛用于估计WPHM的未知参数。 在实际中，一个机械设备有时会运转直至失效，有时会在失效前进行维修，因此数据常常包括失效时间和删失时间。为同时处理这两类数据，似然函数定义为

(13)

其中：n为失效样本个数；m为删失样本个数。

将式(11)和式 (12) 代到式(13)中，其对数似然函数可化简为

(14)

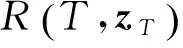
(15)

其中：R0为失效阈值。

剩余寿命误差定义为

(16)

其中：Tp为预测的剩余寿命；Ta为实际剩余寿命。

2 方法步骤

本方法的具体流程如图1所示。

图1 方法流程图Fig.1 Flowchart of the proposed method

具体步骤如下。

1) 选择特征参数：从训练轴承寿命周期数据中提取全寿命周期的时域特征、频域特征和时频域特征参数，从中筛选出能反映轴承性能退化过程的特征参数，构成特征向量。

2) 构建高维训练相对特征集：提取训练轴承的寿命周期样本点，构建相对高维训练特征集。

3) KPCA降维：对高维训练相对特征集进行KPCA降维，选取累计贡献率大于85%的核主元和对应的特征向量。

4) 验证轴承性能退化趋势：构建高维试验相对特征集，通过特征向量映射，得到试验轴承的核主元，验证其能否能够充分表征轴承性能退化过程，若满足，即可将核主元作为WPHM的协变量。

5) 估计模型参数：将训练轴承的核主元作为WPHM的协变量来估计模型的未知参数。

6) 评估可靠性和预测剩余寿命：将试验轴承的核主元作为WPHM的协变量来进行可靠性评估和剩余寿命预测。

3 协变量选取方法

3.1 滚动轴承试验台介绍

本研究中滚动轴承全寿命周期试验数据由美国辛辛那提大学智能系统维护中心(IMS)中心提供[19]。全寿命周期试验台装置如图2所示。

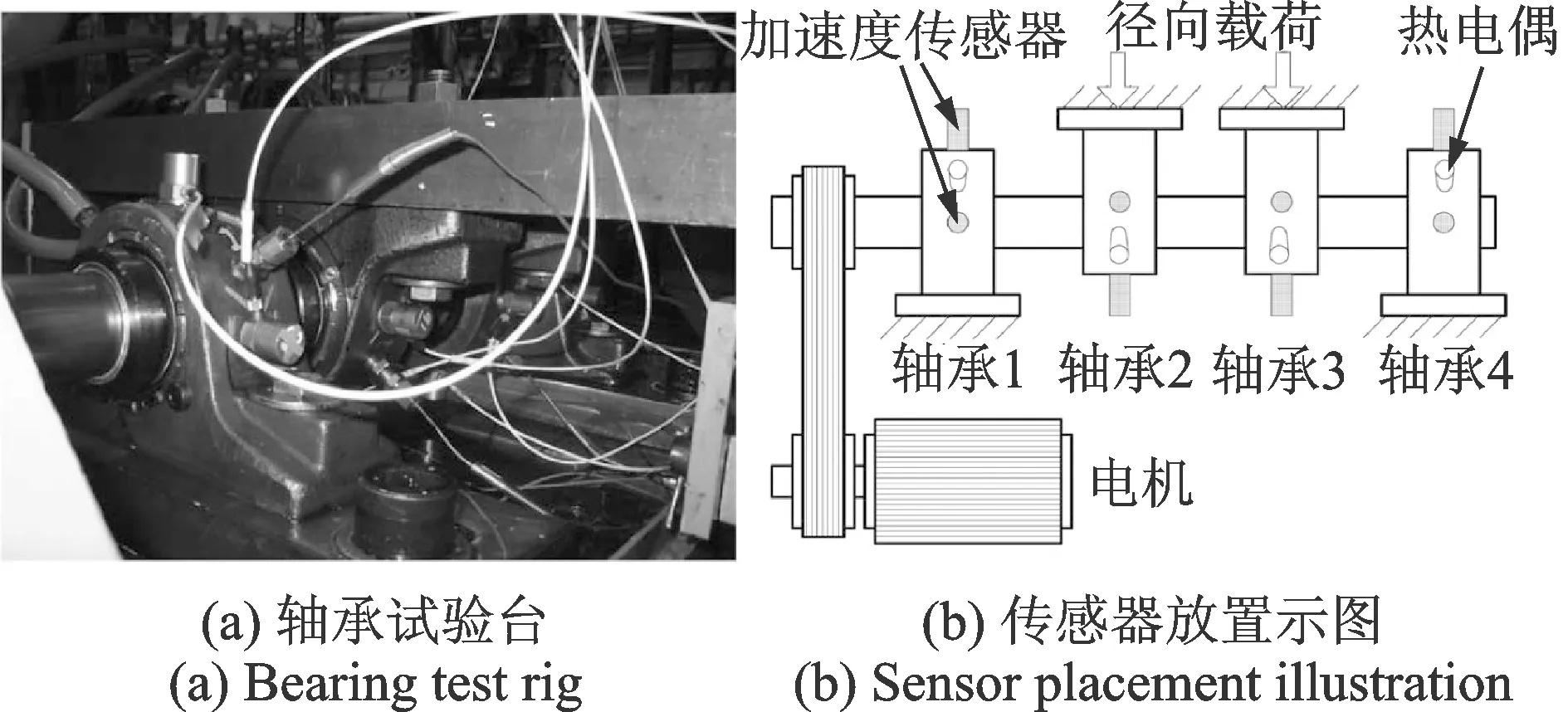
图2 试验台和装置示意图Fig.2 Bearing test rig and sensor placement illustration

在同一轴上安装有4个Rexnord ZA-2115滚动轴承，由直流电机通过皮带联接驱动，轴转速始终保持在2kr/min，轴和轴承共同承受来自弹簧机构施加的26.67kN径向荷载。在油反馈管道安装有磁性螺塞，收集润滑油的碎屑用以验证轴承的性能退化。系统电器开关关闭由磁性螺塞所吸附的金属碎屑量决定，随着轴承性能不断退化，当吸附的碎屑量达到预先设定的阈值，数据采集工作便停止。每个轴承的水平方向和竖直方向各装一个PCB 353B33加速度传感器。振动信号通过美国国家仪器(NI)公司的DAQCardTM-5052E数据采集卡每20 min采集一次，采样率为20kHz，采样点数为20 480个点。试验结果如表1所示。

表1 试验结果

a为内环故障；b为滚动体故障；c为外环故障

以3号轴承(试验1)数据作为试验轴承，其他7个轴承(试验1和试验2)数据作为训练轴承。

3.2 滚动轴承性能退化高维特征集构建

针对7个训练轴承的寿命周期数据，提取各自的时域、频域及时频域等70多个特征参数[20-21]。如果直接对这70多个特征参数进行核主元分析，由于包含大量冗余信息及无用信息，降维后前3个核主元的累计贡献率很低，包含的有用信息较少。为使前几个核主元包含尽可能多的信息，须在进行核主元降维前，保证各维度信息有效性的条件下尽量减少维度。首先，对每个特征绘制随时间变化的全寿命特征图，剔除不能反映退化过程的特征，例如均值、偏斜度等；然后，针对功能或意义相似的特征，通过对比剔除反映性能退化过程效果相对差的特征，例如小波包归一化能量谱与经验模态分解(empirical mode decomposition, 简称EMD)归一化能量谱对比，剔除EMD归一化能量谱等。得到如下11个最能反映轴承性能退化过程的特征参数：

1) 时域包含均方根值、峭度、峰峰值及峰值因子；

2) 频域包含频谱均值、频谱方差及频谱均方根值；

3) 时频域包含3层小波包分解的第3频带归一化小波包能量谱(E3)和第7频带归一化小波包能量谱(E7)，以及第3频带样本熵(S3)和第7频带样本熵(S7)。

考虑到各个轴承制造、安装和实际工况的差异，即使是处于同一工作环境下的同型号轴承，特征参数存在一定的差异。以时域特征参数为例，对1～8号轴承，各自提取正常工作期内一段趋势平稳的时域特征参数，然后求取平均值，如图3所示。

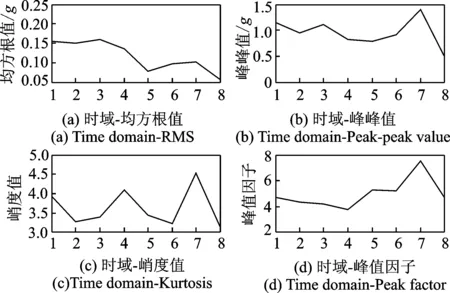
图3 正常期平均时域特征参数Fig.3 The mean time domain features in normal work period

由图3可以明显看出，8个轴承平稳期的时域参数有很大差异。例如图3(a)中，1号轴承正常工作期的平均均方根值为0.154，而5号轴承正常工作期的平均均方根值为0.077。为了降低轴承间特征参数的影响，需要对轴承特征参数进行标准化。首先，选取正常期内一段趋势平稳的特征参数，将该段平均值定为标准值；然后，计算原始特征参数与标准值之比，得到相对特征参数。

对7个训练轴承，每个轴承取100个样本点(每个轴承根据其全寿命过程，选取能反映寿命过程的100个点)，共计700个样本点，构成最终的700×11(11为特征参数个数)的高维训练相对特征集。

对于试验轴承，全寿命周期共有2 152个采样点，构成2 152×11的高维试验相对特征集，如图4所示。其中：(a)～(d)为时域特征；(e)～(g)为频域特征；(h)～(i)为小波包第3，7频带归一化能量谱；(j)～(k)为小波包第3，7频带样本熵；(l)表示全寿命周期轴承数据采集连续情况，间断点为空数据，在此时间内未进行数据采集。

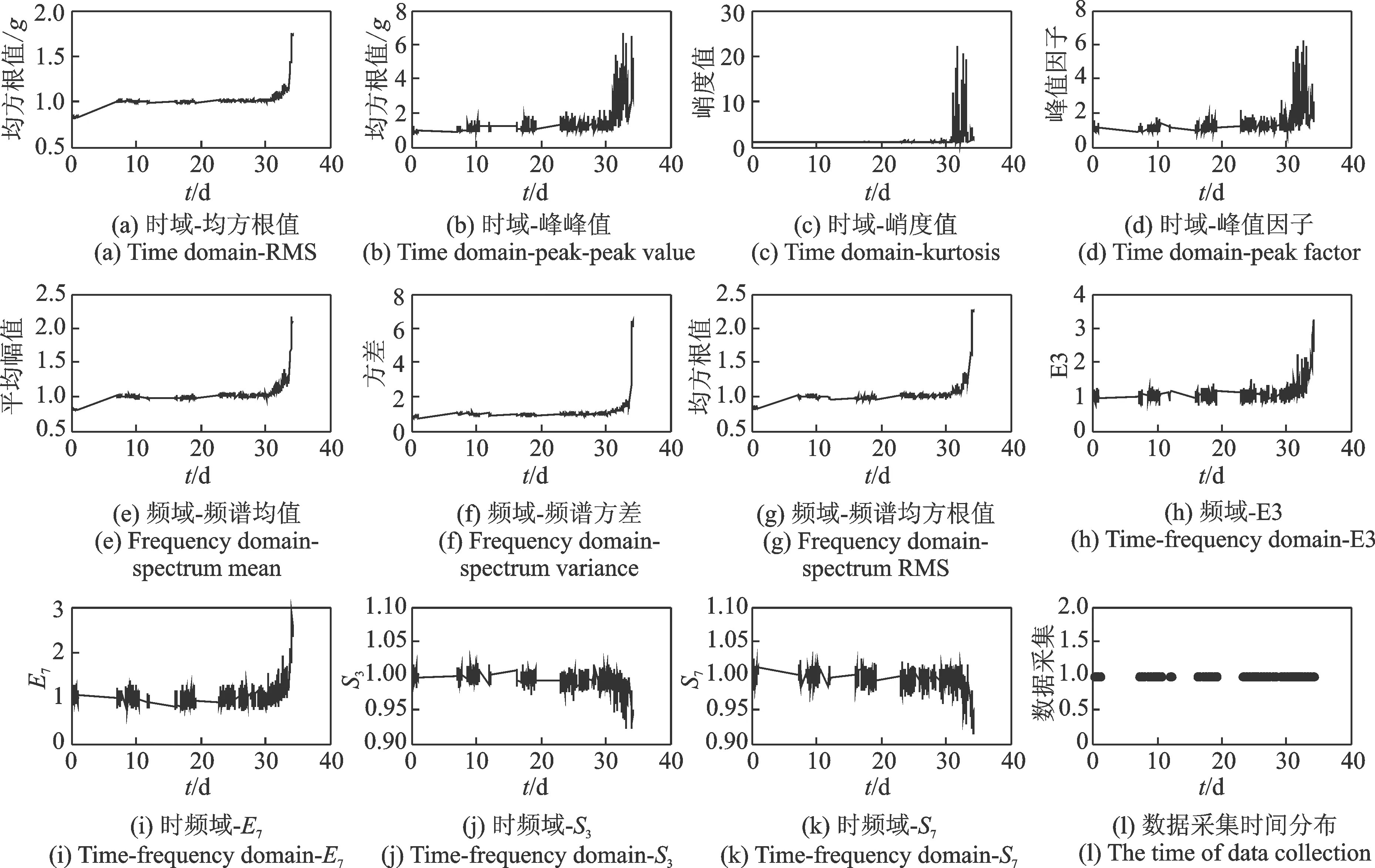
图4 高维试验相对特征集Fig.4 High test relative feature set

3.3 滚动轴承核主元的性能退化评估

分别对特征参数未相对化的高维训练绝对特征集和特征参数相对化的高维训练相对特征集进行核主元分析(σ=57)，前3个核主元的特征值和累计贡献率如表2所示。

表2 核主元分析结果对比

由表2可见，直接对高维训练绝对特征集进行分析，由于轴承制造、安装和工况差异引起数据离散较大，造成前3个核主元的累计贡献率明显低于高维训练相对特征集累计贡献率，即前者降维效果低于后者，因此选择高维训练相对特征集进行核主元分析。

选取前3个核主元特征值对应的特征向量组成投影空间，对高维试验相对特征集进行中心化后投影，得到高维试验相对特征集的核主元。为验证核主元分析效果，将高维试验相对特征集第1至第3核主元投影到三维空间，第1和第2核主元投影到二维空间，分别如图5所示，图中点的位置信息如表3所示。

试验轴承的第1核主元KPC1的贡献率为63.24%，包含了高维试验相对特征集的大部分信息，因此在图5中可以区分轴承性能退化过程的各个阶段；第2核主元KPC2和第3核主元KPC3的贡献率分别为17.47%和8.49%，包含了高维试验相对特征集的少部分信息，因此能区分轴承性能退化的部分阶段。从图5中可以清晰区分出正常工作期、早期故障期、磨损中期和急剧后期，其中经常忽略的恢复期也能在图5中清晰识别。此外，随着时间变化，数据点总体上有明显的趋势走向规律，且变化过程比较平滑。

表3 点的位置信息

图5 核主元投影Fig.5 Kernel principal component projection

为与WPHM常规协变量进行对比，将试验轴承全寿命周期的均方根值和峭度投影到二维空间，如图6所示。从图中可以看出：均方根值虽然能够区分正常工作期、早期故障期、磨损中期和急剧后期，但其仅是时域中的一个特征参数，从包含的特征信息量上来看，远没有核主元包含的信息多，稳定性远低于核主元；峭度值仅对早期故障期区分比较明显，无法区分轴承性能退化过程的其他阶段，且早期故障数据变化范围非常大且随时间不停振荡；而在磨损中期和急剧后期只是比正常工作期略微增大，更适合作为早期故障预警的重要指标，而不能反映性能退化的过程。

图6 均方根值、峭度投影Fig.6 RMS and Kurtosis projection

相比前3个核主元包含了时域、频域、时频域的绝大部分信息，同时在变化趋势方面，图5的数据点变化比图6更加平滑，轴承性能退化过程总体趋势走向更加明显。比如在31.05～33.34 d的早期故障期，由于峰峰值、峭度值及峰值因子等变化范围非常大(图4)，故图5中早期故障期数据点有相对明显的偏移，但相对图6变化趋势更平滑、偏移更小。又如33.49～34.17 d的磨损中期和急剧后期，图5数据点的总体趋势走向比图6更加明显。整体上来说，随着时间的变化，图5的数据点过渡比图6更加平滑，偏移更小。

综上，由于前3个核主元包含时域、频域及时频域绝大部分信息，且兼顾非线性成分，样本点间偏离性相对较小，数据点有明显的趋势走向，因此选择能充分表征轴承性能退化过程的前3个核主元作为WPHM模型的协变量来建立模型更加稳定可靠。

4 剩余寿命预测

4.1 可靠性评估

将高维训练相对特征集中核主元的各轴承全寿命数据和删失数据带入式(14)中，求解模型未知参数的估计值，如表4所示。

表4 WPHM参数

将高维试验相对特征集的核主元带入式(11)计算可靠度，如图7所示。

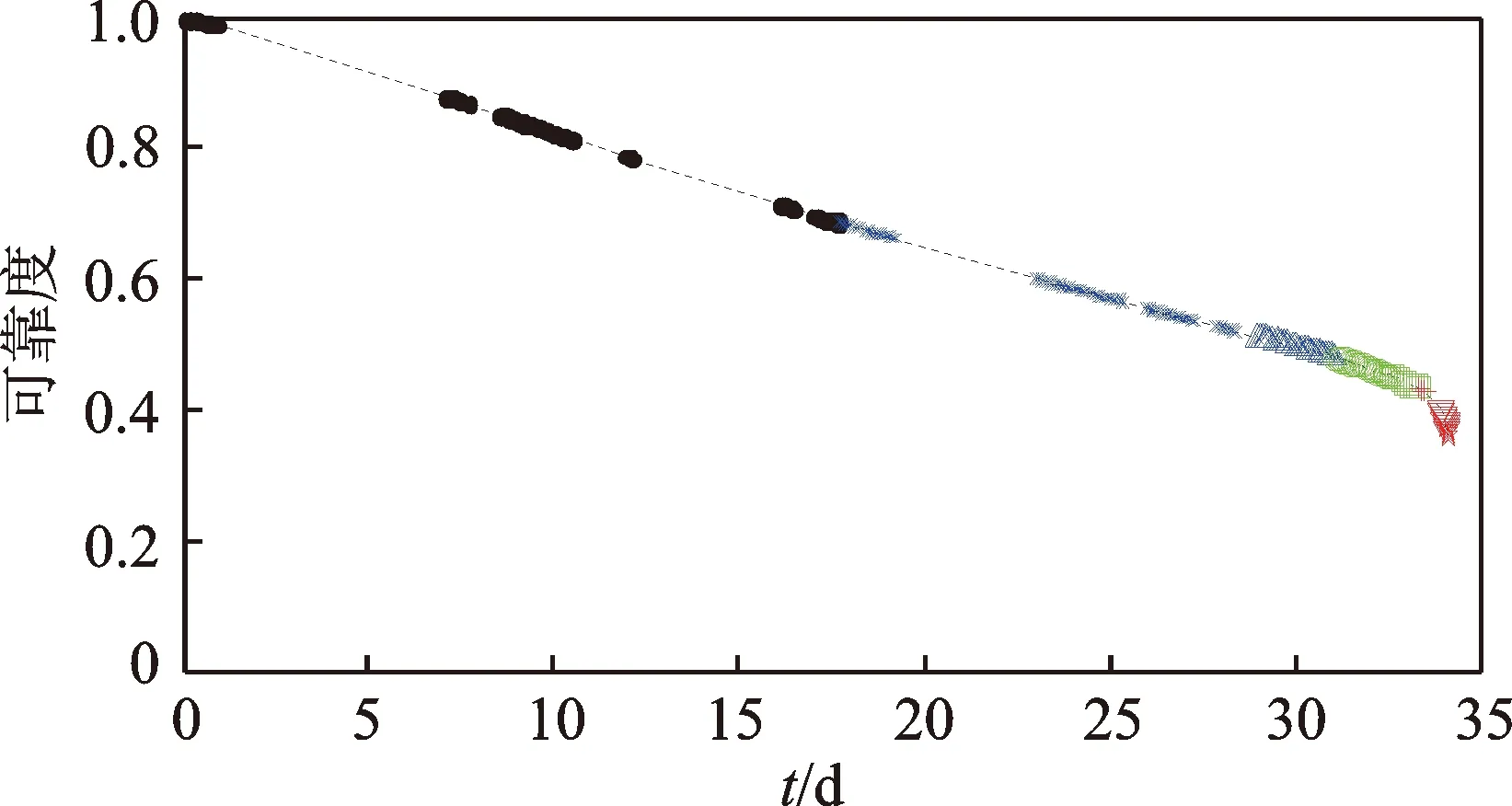
图7 全寿命周期可靠度Fig.7 The reliability of lifetime

由图7可以看出，在正常工作期可靠度的下降速度基本保持不变。早期故障期的下降速度开始增大，磨损中期和急剧磨损期的下降速度急剧增大。由于模型中的协变量是时变性的，任一时刻的可靠度都由历史数据的累积计算得到，不会因为某时刻采集数据突变而突变(如恢复期)，其可信度高于那些仅仅与当前时间有关计算得到的可靠度模型。从可靠度下降趋势变化就能准确区分轴承性能退化的状态。

4.2 剩余寿命预测

为了验证剩余寿命预测方法的准确度，需设置可靠度阈值。它一般由统计学经验设定。由于式(11)中协变量是时变性的，且e-1为特征寿命[23]，由图7可以看出，急剧后期的可靠度值在e-1左右。因此可靠度阈值R0设置为e-1。当然，定义的可靠度阈值并非恒定的，需要依据历史数据的可靠度和设备维修经验来适当的调整。

针对试验轴承，不同退化时期共取4个时间点，预测其剩余寿命，结果如表5所示。依据式(16)得到对应的误差率，如图8所示。可以看出，正常工作期的剩余寿命预测值与真实剩余寿命差别很大，这是因为轴承产生损伤是偶发性的，正常期各项特征处于正常范围内，协变量预测趋势呈线性，以至于正常期的预测误差较大。随着步入早期故障，新退化特征的累积，协变量的预测曲线会越来越准确，剩余寿命预测值也越来越接近真实的剩余寿命，到磨损中期的33.986 8 d的误差率为9.84%(即准确度为1-9.84%= 90.16%)。结果表明，提出的寿命方法可以准确地预测轴承的剩余寿命，以便及时提供有效的维修决议。

表5 剩余寿命预测

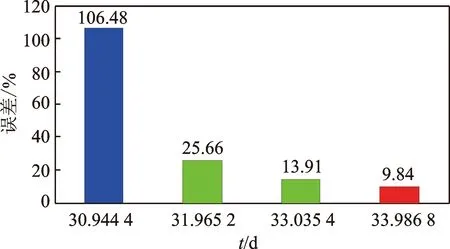
图8 剩余寿命预测误差度Fig.8 The error percent of RUL prediction

5 结 论

1) 基于相对多特征的核主元分析方法，降维后的核主元能够充分表征轴承性能退化过程。

2) 以包含多域信息的核主元作为WPHM协变量，能够准确预测轴承的剩余寿命，及时提供有效的维修决议，极大地优化了WPHM协变量选取的方法。

3) 相对特征降低了轴承制造、安装和实际工况差异的影响，大大增强了该方法的适用性和稳定性。增加新的训练轴承全寿命数据不会引起数据离散，且对新的监测样本求取相对特征，映射后带入模型即可求取可靠度和剩余寿命，为维修计划提供有力的支持。

[1] 郭红.内外膜独立供油径推联合浮环轴承性能分析与实验研究[D].上海：上海交通大学,2009.

[2] Wei Guo, Peter W. A novel signal compression method based on optimal ensemble empirical mode decomposition for bearing vibration signals [J]. Journal of Sound and Vibration, 2013,332(2): 423-441.

[3] Cong Feiyun, Chen Jin, Dong Guangming, et al. Vibration model of rolling element bearings in a rotor-bearing system for fault diagnosis [J]. Journal of Sound and Vibration, 2013,332 (8): 2081-2097.

[4] 张小丽,陈雪峰,李兵,等. 机械重大装备寿命预测综述[J]. 机械工程学报, 2011,47(11): 100-116.

Zhang Xiaoli, Chen Xuefeng, Li Bing, et al. Review on life prediction of machinery major equipment [J]. Chinese Journal of Mechanical Engineering, 2011, 47 (11): 100-116. (in Chinese)

[5] Cox D R. Regression models and life-tables (with discussion) [J]. Journal of the Royal Statistical Society, Series B: Methodological, 1972,34(2): 187-220.

[6] 丁锋,何正嘉,訾艳阳,等. 基于设备状态振动特征的比例故障率模型可靠性评估[J]. 机械工程学报, 2009, 45 (12): 89-94.

Ding Feng, He Zhengjia, Zi Yanyang, et al. Reliability assessment based on equipment condition vibration feature using proportional hazards model [J]. Chinese Journal of Mechanical Engineering, 2009, 45 (12): 89-94. (in Chinese)

[7] Zhang Chao, Wang Shaoping, Bai Guanghan.An accelerated life test model for solid lubricated bearings based on dependence analysis and proportional hazard effect[J].Acta Astronautica,2014,95(1): 30-36.

[8] Zhang Qing, Hua Cheng, Xu Guanghua. A mixture Weibull proportional hazard model for mechanical system failure prediction utilising lifetime and monitoring data [J]. Mechanical Systems and Signal Processing, 2014, 43 (1-2): 103-112.

[9] Janjarasjitt S, Ocak H, Loparo K. Bearing condition diagnosis and prognosis using applied nonlinear dynamical analysis of machine vibration signal [J]. Journal of Sound and Vibration, 2008, 317 (1-2): 112-126.

[10]Scholkopf B, Smola A, Muller k R. Nonlinear component analysis as a kernel eigenvalue problem [J].Neural Computation,1998, 10 (5): 1299-1319.

[11]Liu Wenbin, He Yuxin, Wang Huaqing, et al. Bearing condition recognition based on kernel principal component analysis and genetic programming [J].Applied Mechanics and Materials, 2013, 397-400(1): 1282-1285.

[12]李巍华,廖广兰,史铁林. 核函数主元分析及其在齿轮故障诊断中的应用[J]. 机械工程学报,2003(8):65-70.

Li Weihua, Liao Guanglan, Shi Tielin. Kernel principal component analysis and its application in gear fault diagnosis [J]. Chinese Journal of Mechanical Engineering,2003(8):65-70.(in Chinese)

[13]Lee J, Yoo C, Choi S, et al. Nonlinear process monitoring using kernel principal component analysis [J]. Chemical Engineering Science, 2004, 59 (1)：223-234.

[14]He Qingbo, Yan Ruiqiang, Kong Fanrang, et al. Machine condition monitoring using principal component representations [J]. Mechanical Systems and Signal Processing, 2009, 29 (2): 446-466.

[15]胡金海,谢寿生, 侯胜利,等. 核函数主元分析及其在故障特征提取中的应用[J]. 振动、测试与诊断, 2007, 27 (1): 48-52.

Hu Jinhai, Xie Shousheng, Hou Shengli, et al. Kernel principal component analysis and its application to fault feature extraction [J] Journal of Vibration, Measurement & Diagnosis, 2007, 27 (1): 48-52. (in Chinese)

[16]李学军,李平, 蒋玲莉,等. 类均值核主元分析法及在故障诊断中的应用[J]. 机械工程学报, 2004, 50 (3): 123-129.

Li Xuejun, Li Ping, Jiang Lingli, et al.Class mean kernel principal component analysis and its application in fault diagnosis [J]. Chinese Journal of Mechanical Engineering, 2004, 50 (3): 123-129. (in Chinese)

[17]王新峰,邱静,刘冠军. 核主元分析中核函数参数选优方法研究[J]. 振动、测试与诊断, 2007, 27 (1)：62-64.

Wang Xinfeng, Qiu Jing, Liu Guanjin. The study on the parameter selection of kernel function in kernel principal component analysis [J]. Journal of Vibration, Measurement & Diagnosis, 2007, 27 (1):62-64. (in Chinese)

[18]Lagarias J, Reeds J, Wright M, et al. Convergence properties of the Nelder-Mead simplex method in low dimensions [J]. Society for Industrial and Applied Mathematics Journal on Optimization, 1998, 9 (1): 112-147.

[19]Qiu Hai,Lee J A Y, Lin Jiang, et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics [J]. Journal of Sound and Vibration, 2006, 289 (4-5): 1066-1090.

[20]Wang Fengtao, Sun Jian, Yan Dawen. A feature extraction method for fault classification of rolling bearing based on PCA [J].Journal of Physics: Conference Series, 2015, 628(1):1-7.

[21]苏文胜,王奉涛,朱泓,等. 基于小波包样本熵的滚动轴承故障特征提取[J]. 振动、测试与诊断, 2011,31(2) ：162-166.

Su Wensheng, Wang Fengtao, Zhu Hong, et al. Study on the feature extraction of rolling element bearing fault based on wavelet packet sample entropy [J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(2): 162-166. (in Chinese)

[22]Williams T, Ribadeneira X, Billington S, et al. Rolling element bearing diagnostics in run-to-failure lifetime testing [J].Mechanical Systems and Signal Processing, 2001, 15(5): 979-993.

[23]张志华. 可靠性理论及工程应用[M]. 北京: 科学出版社, 2012: 9-10.

10.16450/j.cnki.issn.1004-6801.2017.03.009

国家自然科学基金资助项目(51375067);航空科学基金资助项目(20132163010)

2016-12-30；

2017-03-15

TH165.3; TH17

王奉涛，男，1974年2月生，博士、副教授。主要研究方向为设备状态监测与故障诊断、振动与噪声。曾发表《基于流形-奇异值熵的滚动轴承故障特征提取》(《振动、测试与诊断》2016年第36卷第2期)等论文。 E-mail：wangft@dlut.edu.cn