高中数学函数单调性教学中学生思维能力提升方法

（广西壮族自治区梧州市藤县第一中学）

摘 要：在高中数学教学中，培养学生思维能力一直都是一项重要的教学任务。特别是在学习函数单调性这一模块的知识时，学生只有拥有了一定程度上的思维能力和思维习惯，才能对这一模块的知识理解得更加深入、更加透彻，从而能够在练习中不断地提升自己的思维能力以及应用技巧。

关键词：高中数学；函数单调性；思维能力；提升方法

函数单调性，简单来说，就是在某一个区间上自变量在函数的增减变化中，函数值的变化规律。高中数学中的函数单调性是比学生在初中接触到的函数知识还要高上一个知识层面的学科内容，同时它作为学生在高中数学学习过程中需要掌握的第一个函数的性质，函数单调性也可以被称为函数的增减性，当f（x）的自变量在定义的区间增大或减小时，f（x）本身也随之增大或减小。在进行函数单调性的学习过程中，教师可以通过创设情境、合理设计作业以及开展数学活动的方式，提升学生对函数单调性的理解，从而提升学生学习函数单调性的思维能力。

一、创设生活化情境教学，提升初步认识

教师通过创设一个符合生活实际的教学情境，能够很好地将学生带入这一情境中，使学生产生浓厚的学习兴趣，并激发学生强烈的求知欲望。数学虽然具有抽象性和严谨的逻辑性，但不可否认的是，数学也是来源于生活的学科，很多理论、概念、公式都是由于生活中的现象经过精确研究计算和推导而得到的，其目的也在于服务生活实际。因此，教师只要在课堂中创造一个符合生活实际的数学函数单调性情境，就能够有效地提升课堂教学效率。

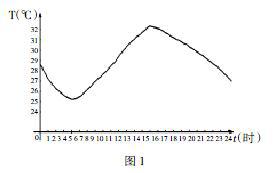
例如，教师以北京奥运会的开幕式为例，通过创设生活化情境的方式提升学生的函数单调性思维能力。教师在课前先布置任务：①由于某种原因，2008年北京奥运会开幕式时间由原定的7月25日推迟到8月8日，请查阅资料说明做出这个决定的主要原因；②通过查阅历史资料研究北京奥运会开幕式当天气温变化情况。通过课堂交流可以得知，开幕式推迟主要是天气的原因，北京的天气到8月中旬，平均气温、平均降雨量和平均降雨天数等均开始下降，比较适宜大型国际体育赛事。那么北京市在8月8日一整天的气温变化就可以用一张曲线图表示，如图1所示。

此时教师应引导学生捕捉重要信息，然后启发学生的思维。

问题1：请同学们观察图，指出该天的气温在如何变化？此题由学生独立思考，不得进行讨论。

问题2：还能举出生活中其他的数据变化情况吗？

对于问题1来说，是典型的通过生活实例，让学生对图象的上升和下降有一个初步的感性认识，让学生感受函数的单调性和我们的生活密切相关，进而激发学生的兴趣，引发学生进一步学习的好奇心。某学生对问题1的回答是：当时间在0～4时，温度呈下降趋势；当时间在4～14时，温度呈上升趋势；当时间在14～24时，温度呈下降趋势。

对于问题2来说，学生可能会由此联想到水位高低、油价波动以及股票波动等等。

对这一案例的归纳为：通过函数单调性的思维，明白了随着自变量的变化，函数值是变大还是变小。而这样设计情境的核心在于通过生活情境进入课堂，以引起学生兴趣。

二、设计综合性的习题作业，培养思维组织性和发散性

高中函数单调性这一模块的知识不仅牵涉到学生在初中所接触的函数知识，还涉及一些对于学生自主学习而言较为复杂和困难的知识，这些知识看似独立，但又有着极其密切的联系，而学生想要掌握这些知识间的关联性，就需要拥有数学思维能力中的组织性和发散性。为此，教师必须引导学生将已经掌握的知识进行条理清晰、层次分明的整理和归纳，完善学生思维能力的组织性，其次还要引导学生能够学会从多个角度去思考问题，促使思维发散性得到提升的空间。

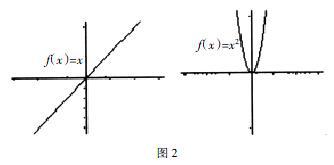
例如：画出y=x和y=x2的函数图象，回答下面两个问题。

问题1：分别指出上面两个函数的图象在哪个区间是上升的，在哪个区间是下降的？

问题2：同学们能用数学语言把这两个函数图象“上升”或“下降”的特征描述出来吗？

对于问题1，可以将两个函数图象画出来，如图2所示。

（左为y=x，右为y=x2）

某学生在作业中这样描述：一次函数的定义域呈整体上升趋势，二次函数呈先下降后上升趋势。教师应评价，这样定义是否准确？另一学生这样回答：一次函数y=x在区间（-∞，+∞）上是“上升”的；二次函数y=x2在区间（-∞，0）上是“下降”的，（0，-∞）上是“上升”的。教师同样进行评价。

对于问题2，学生可能会显得思维混乱，难以下手。此时教师可以通过几何画板将y=x展示出来，显示A点的运动情况，使学生理解x、y的变化。此时，教师应及时提问：请用语言表示y=x图象的“上升”特征。某学生回答：该函数随着x值的增大，y值相应增大。教师要学生评价该生的回答是否准确。另一学生补充回答：该函数在区间（-∞，+∞）上随着x值的增大，y值相应增大。教师应对这名学生的补充回答予以肯定。再提问：函数y=x2呢？第三名学生回答：函数y=x2在区间（-∞，0）上随着x值的增大，y值相应减小；在区间（0，+∞）上是随着x值的增大，y值相應增大。教师最后补充：在数学上，我们把y随着x值的增大而增大，称为增函数；把y随着x值的增大而减小，称为减函数。

三、开展比较分析的教学活动，提升学生数学思维能力

比较分析在学生的生活中很常见，教师可以通过数学活动的方式，引导学生对函数单调性进行比较分析，提升学生的数学思维能力。此外，教师还需要引导学生进行及时的反思。反思作为一种能够较好地促进学生掌握学习方法、养成良好思维方式的学习意识，在比较分析教学中也能够得到较好的运用，这样不仅能促进学生养成比较分析的解题思路，还能提升学生的思维能力。

高中数学函数单调性这一模块的知识作为当前高中生必须掌握的知识点，教师在教学中必须将学生放在主体地位上，利用一切有效的教学方式，激发学生的探究欲望，并设计针对性的习题训练，培养学生思维能力的组织性和发散性，在解决学习困难时引入比较分析法，加强学生对概念性知识的理解程度，最后还需要引导学生对自己的学习过程进行反思，及时发现自身思维方式上的缺陷和学习能力上的问题，以此提高学生的学习效率和教师的教学质量。

参考文献：

[1]崔兴清.关于高中数学函数单调性的教学探讨[J].新课程（中旬），2015（3）：103.

[2]陆华.关于高中数学函数单调性的教学探讨[J].教育观察（下半月），2016，5（5）：59-60.

[3]孙月.对高中函数单调性的解析策略研究[J].新课程（中学），2015（10）：68.

作者简介：韦杰雄（1974—），男，汉族，广西藤县人，中学一级教师，研究方向为高中数学基础函数教学。

编辑 温雪莲