再论Devaney混沌的随机性质

张新敏

(西南石油大学理学院， 四川成都610500)

再论Devaney混沌的随机性质

张新敏

(西南石油大学理学院， 四川成都610500)

拓扑动力系统相关动力性质(如弱混合、拓扑弱混合、敏感性)之间的关系一直是动力系统研究的主要问题。证明利用相关函数定义的弱混合拓扑动力系统必为拓扑弱混合。以此为基础，得到的系统是multi-敏感的和初值敏感依赖的。从而改进了相关文献的主要结果。

弱混合；拓扑弱混合；multi-敏感

引言

贯穿全文，记N={1,2,3,…}，Z+={0,1,2,…}。设(X,d)为非平凡的紧致度量空间，映射f:X→X连续，则称(X,f)为一动力系统。对动力系统混沌行为的数学研究始于Li T Y和Yorke J A[1]，即后来为大家所熟知的Li-Yorke混沌。简而言之，混沌是指系统在沿着时间维度演变的过程中，其微观个体的状态相对于人们预测能力而言的不确定性；它是系统复杂性的重要量度。基于学者们对于复杂性的不同理解，各种各样的混沌定义层出不穷，如Li-Yorke混沌、Devaney混沌、稠混沌、全局混沌、分布混沌、Li-Yorke敏感。其中，比较有影响力的是Devaney混沌。

混沌另外一个显著的特征是对初值的敏感依赖性。称动力系统(X,f)是初值敏感依赖的，如果存在ε>0，使得对任意x∈X及任意δ>0，存在y∈B(x,δ):={y∈X:d(x,y)<δ}及n∈Z+，满足d(fn(x),fn(y))>ε。

定义1[2]称动力系统(X,f)是Devaney混沌的， 如果以下条件得到满足：

(1) (X,f)是拓扑传递的，即对任意非空开子集U,V⊂X，存在n∈Z+，使得fn(U)∩V≠φ；

(2)f的周期点在X中稠密；

(3) (X,f)是初值敏感依赖的。

值得注意的是，Banks等[3]证明了周期点稠密的拓扑传递系统是初值敏感依赖的。文献[4]得到了几乎周期点稠密的拓扑传递系统是初值敏感依赖的。后来，Moothathu[5]引入了更广义的敏感性——syndetic-敏感、cofinite-敏感和multi-敏感。同时证明了非极小的syndetic-传递系统是syndetic-敏感的，并且对于syndetic-传递系统，初值敏感依赖蕴含syndetic-敏感。近来，吴新星等[6]得到了乘积系统是multi-敏感的当且仅当存在某个因子系统multi-敏感的。

集合A={a10，使得对任意i∈N，ai+1-ai≤L。全体syndetic集记为Fs。

集合A⊂Z+是thick的，如果它包含任意长的整数段，即对任意n∈N，存在an∈A，使得{an,an+1,…,an+n}⊂A。全体thick集记为Ft。

对任意U⊂X及任意δ>0，定义

Nf(U,δ)={n∈Z+:diam(fn(U))>δ}

定义2[5]称动力系统(X,f)是

(1) syndetic-敏感的，如果存在δ>0，使得Nf(U,δ)∈Fs。

(2) cofinite-敏感的，如果存在δ>0，使得Nf(U,δ)为有限余的。

(3) multi-敏感的，如果存在δ>0，使得对任意n∈及任意n个非空开子集U1,…,Un⊂X，恒有φ。

1预备知识

如果U,V⊂X，定义回复时间集为

N(U,V)={n∈Z+:fn(U)∩V≠φ}= {n∈Z+:f-n(V)∩U≠φ}

如果乘积系统(X×X,f×f)是拓扑传递的，则称动力系统(X,f)是拓扑弱混合的。

下面命题给出了拓扑弱混合的若干等价刻画：

引理1[7]设(X,f)为动力系统，则以下命题等价：

(1) (X,f)是弱混合的；

(2) 对任意非空开子集U,V⊂X，N(U,U)∩N(U,V)≠φ；

(3) 对任意非空开子集U,V⊂X，N(U,U)∩N(V,U)≠φ；

(4) 对任意非空开子集U,V⊂X，N(U,V)为thick集；

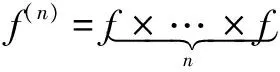
设μ为(X,d)上的Borel-概率测度，满足supp(μ)=X，其中supp(μ)表示测度μ的支撑。 对于定义在X上的连续函数φ,φ，定义它们的相关函数为：

Cφ,φ(n)=∫X(φ°fn)φdμ-∫Xφdμ∫Xφdμ。

Xu Z J等[8]于2004年证明了强混合的动力系统必为拓扑传递和初值敏感依赖的。近来，王涛和贾诺[9]改进了该结果，得到弱混合的动力系统是拓扑传递的; 如果附加周期点稠密性，则该系统必为初值敏感依赖的。吴新星和朱培勇[10-11]系统研究了连续区间映射的敏感依赖性。冯汉等[12-13]研究了动力系统的一些混沌性质及其应用。近来，李瑞佳和朱培勇[14]得到了强传递集的一些基本性质。本文以文献[8-9]为基础，进一步证明了弱混合的的动力系统是拓扑弱混合和multi-敏感的。从而改进了文献[8-9]的主要结论。同时，该结果更加深入地阐述了弱混合和拓扑弱混合之间的联系。

2主要结果

定理1如果动力系统(X,f)是弱混合的，则(X,f)是拓扑弱混合的。

证明任取X的非空开子集U，V，同时令ε=μ(U)μ(V)。由测度μ的正则性(文献[15]定理6.1)知，存在非空闭子集A⊂U，B⊂V，使得μ(A)μ(B)>7ε/8。同时注意到X为正规空间， 由Urysohn-引理得存在连续函数φ:X→ [0,1]和φ:X→[0,1]，使得如下条件成立

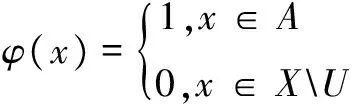
由于(X,f)是弱混合的，所以

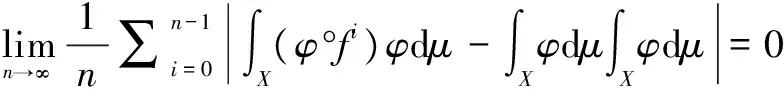
因此

由此结合φ，φ的选取知，

0<∫X(φ°fn)φdμ=∫f-n(V)∩U(φ°fn)φdμ≤μ(f-n(V)∩U)

这说明N(U,V)={n∈Z+:f-n(V)∩U≠φ}⟺P为thick-集(因为P的密度为1)。由引理1自然可得， (X,f)是拓扑弱混合的。

文献[9]定理2证明周期点稠密的弱混合系统是初值敏感依赖的。本文定理2表明，周期点稠密性条件是可去的。文献[5]说明非平凡的拓扑弱混合的系统是multi-敏感的。但是未有证明，为保证本文完整性，给出该结果的详细证明。

定理2如果动力系统(X,f)是弱混合的，则(X,f)是multi-敏感的。特别地，(X,f)是初值敏感依赖的。

证明由定理1知，只须证明拓扑弱混合蕴含multi-敏感性。事实上，由于X为非平凡的空间，所以存在不同的两点x,y∈X。取ε=d(x,y)/4>0，同时取V1=B(x,ε)，V2=B(y,ε)。显然，

dist(V1,V2)=inf{d(z1,z2):z1∈V1,z2∈V2}≥2ε

对任意自然数n，任取n个非空开子集U1,…,Un⊂X，同时令

U=U1×U1×U2×U2×…×Un×Un⊂X2n，V=V1×V2×V1×V2×…×V1×V2⊂X2n

由于f是拓扑弱混合的，由引理1知f(×2n)是拓扑传递的，因此存在m∈Z+，使得

(f(×2n))m(U)∩V≠φ

这说明对任意1≤i≤n，

fm(Ui)∩V1≠φ≠fm(Ui)∩V2

所以diam(fm(Ui))≥2ε,因此，(X,f)是multi-敏感的。

[1] LI T Y,YORKE J A.Period three implies chaos[J].Amer Math Monthly,1975,82:985-992.

[2] DEVANEY R L.An introduction to chaotic dynamical systems[M].Reading:Addison-Wesley,1989.

[3] BANKS J,EROOKS J,CAIRNS G,et al.On Devaney’s definition of chaos[J].Amer Math Monthly,1992,99:332-334.

[4] GLASNER E,WEISS B.Sensitive dependence on initial conditions [J].Nonlinearity,1993,6:1067-1075.

[5] MOOTHATHU T K.Stronger forms of sensitivity for dynamical systems[J].Nonlinearity,2007,20:2115-2126.

[6] WU X,WANG J,CHEN G.F-sensitivity and multi-sensitivity of hyperspatial dynamical systems[J].J Math Anal Appl,2015,429:16-26.

[7] 叶向东,黄文,邵松.拓扑动力系统概论[M].北京:科学出版社,2008.

[8] XU Z J,LIN W,RUAN J.Decay of correlations implies chaos in the sense of Devaney[J].Chaos,Solitons and Fractals,2004,22:305-310.

[9] 王涛,贾诺.Devaney混沌的随机性质[J].数学的实践与认识,2010,40:210-213.

[10] 吴新星,朱培勇.关于连续区间映射的敏感依赖性[J].系统科学与数学,2012(32):215-225.

[11] 吴新星.关于d-跟踪性质的一些注记[J].中国科学:数学,2015,45:273-286.

[12] 冯汉,索宇,朱培勇.基于Logistic映射的迭代式的混沌特性及混沌控制[J].四川理工学院学报:自然科学版,2011,25(1):24-26.

[13] 卢天秀,朱培勇.线性序拓扑空间上不稳定流形的映射性质[J].四川理工学院学报:自然科学版,2009,23(4):32-34.

[14] 李瑞佳,朱培勇.拓扑动力系统中强传递集的一些性质[J].四川理工学院学报:自然科学版,2016,29(6):90-93.

[15] WALTERS P.An Introduction to Ergodic Theory[M].New York:Springer-Verlap Inc.,1982.

Further Study on Stochastic Properties in Devaney’s Chaos

ZHANGXinmin

(School of Sciences, Southwest Petroleum University, Chengdu 610500, China)

The relations among some dynamical properties (for example, weakly mixing, topologically weakly mixing, and sensitivity) are main research for dynamical systems. It is proved that every weakly mixing dynamical system defined using correlation function is topologically weakly mixing. Based on this result, it is obtained that such a system is multi-sensitive and sensitively dependent on initial conditions, improving the main results obtained by Wang Tao and Jia Nuo in 2010.

weakly mixing; topologically weakly mixing; multi-sensitivity

2017-04-11

国家自然科学基金(11601449)；四川省教育厅科学研究基金(14ZB007)

张新敏(1988-)，女，重庆荣昌人，讲师，硕士，主要从事拓扑动力系统方面的研究，(E-mail)zhangxinmin1995@163.com

1673-1549(2017)03-0094-03

10.11863/j.suse.2017.03.19

O189.1

A