任意四边形均匀带电线的空间电势和空间电场计算

邝向军， 贾连宝

(西南科技大学理学院， 四川绵阳621010)

任意四边形均匀带电线的空间电势和空间电场计算

邝向军， 贾连宝

(西南科技大学理学院， 四川绵阳621010)

由位于坐标轴上的均匀带电直线电势表达式出发，给出了均匀带电直线在xy平面内任意空间位置时的电势表达式，然后，利用电场强度与电势梯度的关系，导出了均匀带电直线在xy平面内任意空间位置时的电场强度坐标分量表达式。只需将各个顶点的坐标相应地代入表达式，采取分段计算然后叠加的方法，原则上可以计算任意多边形均匀带电线的电势和电场。实例计算任意四边形均匀带电线的空间电势和空间电场，并讨论了矩形、正方形及其中心轴线上的特殊情况。给出了一个计算任意多边形均匀带电线的普遍方法，具有良好的普适性。所得到的电势分布和电场分布都是空间坐标的函数，具体、准确，便于在工程技术中应用。

任意四边形均匀带电线；分段计算；空间电势；空间电场

引言

一定形状的均匀带电线的空间电势和空间电场计算是电磁学中的一个重要问题，在各种不同的均匀带电线中，具有轴对称性的圆形带电线分布以及与其相关带电体的电势和电场强度的计算研究得比较多[1-9]。矩形和正方形均匀带电线的电势和电场也有研究[10-11]。而对于对称性不高的任意多边形带电线，由于其电势和电场的计算非常复杂，则研究得非常少[12-13]。虽然已经对任意三角形带电线的空间电势和电场进行了计算[12]，但是，该方法不具有普适性。本文从位于坐标轴上的均匀带电直线的电势表达式出发[14]，给出了均匀带电直线在xy平面内任意空间位置时的电势表达式，进而导出了它的电场强度坐标分量表达式。只需将各个顶点的坐标相应地代入该表达式，采取分段计算然后叠加的方法，原则上就可以计算任意多边形均匀带电线的空间电势和电场，具有良好的普适性。实例计算任意四边形均匀带电线的空间电势和空间电场，并讨论了矩形、正方形及其中心轴线上的特殊情况。

1任意位置均匀带电直线的空间电势和空间电场

一均匀带电直线，电荷线密度为λ，长为2l。取带电直线的中点为坐标原点，建立如图1所示的平面坐标系oxy，取无穷远处为电势零点位置，则该带电直线上的dx′在任意场点P(x,y)产生的电势为：

(1)

该均匀带电直线在P(x,y)产生的电势为[14]：

(2)

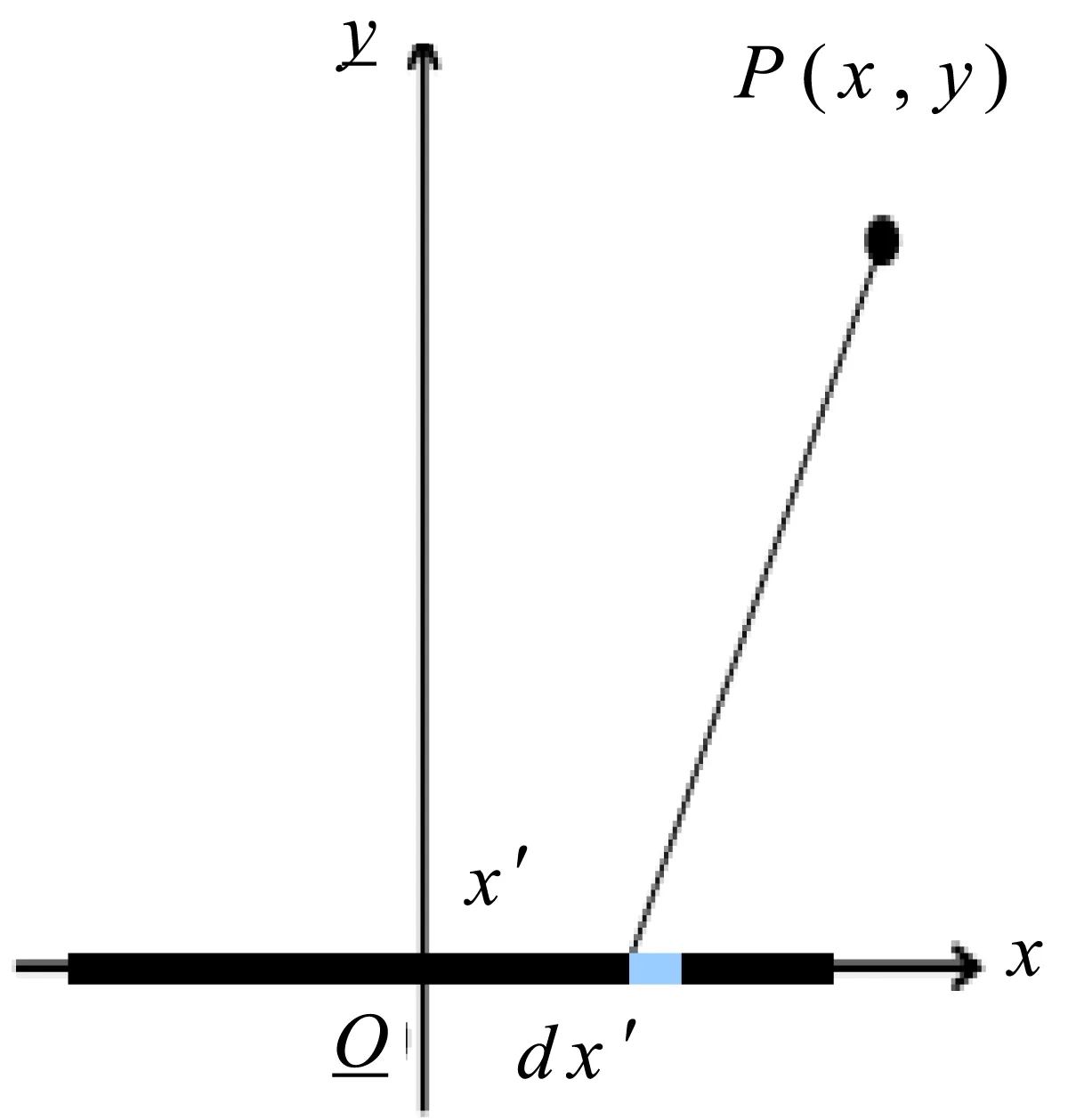
图1有限长均匀带电直线的电势

计算由均匀带电直线组成的带电体的电场时，均匀带电直线未必正好在坐标轴上，因此，需要得到均匀带电直线在空间任意位置时的电势表达式和电场表达式。如图2所示，不失一般性，设均匀带电直线AB位于oxy平面内，两端点的坐标分别为A(x1,y1,0)和B(x2,y2,0)，场点P的坐标为P(x,y,z)，显然有

图2有限长带电直线电场的分量表达式

代入(2)式，有：

(3)

根据电场强度与电势梯度的关系，可得到在空间任意位置时的均匀带电直线的电场强度坐标分量表达式分别为：

(4)

(5)

(6)

2任意四边形均匀带电线的空间电势和空间电场

如图3所示，不失一般性，以任意四边形均匀带电线所在的平面为oxy平面，四个顶点的坐标分别为A(l1,l2,0)、B(l3,l4,0)、C(l5,l6,0)和D(l7,l8,0)，场点坐标为P(x,y,z)，电荷线密度为λ。对AB、BC、CD和DA四条边，分别有：

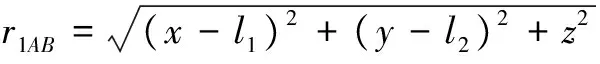
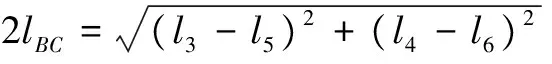
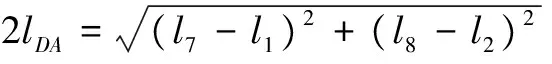
图3均匀带电任意四边形线框的电势和电场

相应地代入(3)式后，可得任意四边形均匀带电线的空间电势为：

(7)

代入式(4)、式(5)和式(6)，可得任意四边形均匀带电线的电场为：

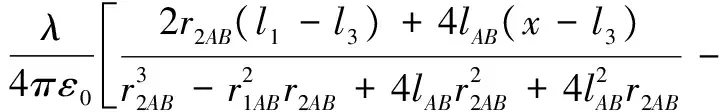
(8)

(9)

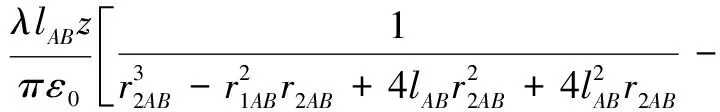
(10)

3讨论

对于长为2l1、宽为2l2矩形线框，l3=l5=-l1，l6=l8=-l2，l4=l2，l7=l1，此时有：

代入(7)式可得矩形均匀带电线的空间电势为：

(11)

代入式(8)、式(9)和式(10)则可得矩形均匀带电线的电场为：

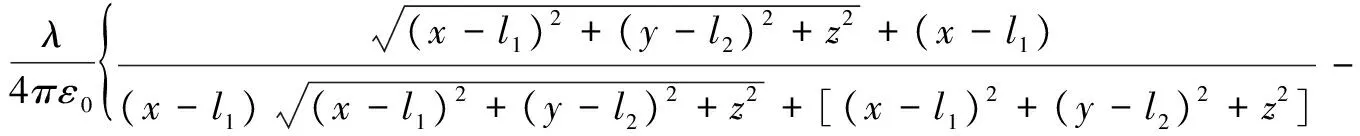
(12)

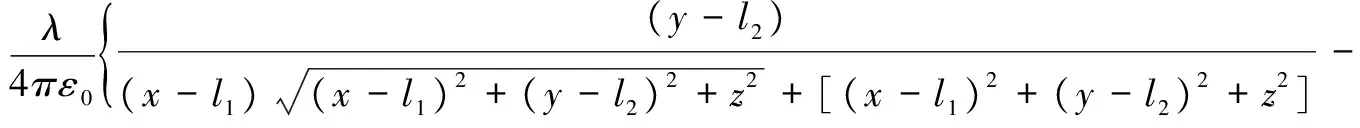
(13)

(14)

若场点P恰好在中心轴线上，则再令x=y=0，可得矩形线框中心轴线上的电势和电场强度分别为：

(15)

EPx=0，

(16)

在上述矩形线框结果的基础上，再令l1=l2=l，就可得到均匀带电正方形线框的空间电势和空间电场分布表达式。若场点P在正方形线框的中心轴线上，则有：

(17)

EPx=0，

(18)

4结束语

本文从位于坐标轴上的均匀带电直线的电势表达式出发，给出了均匀带电直线在xy平面内任意空间位置时的电势表达式，进而利用电场强度与电势梯度的关系，导出了均匀带电直线在xy平面内任意空间位置时的电场强度坐标分量表达式。只需将各个顶点的坐标相应地代入该表达式，采取分段计算然后叠加的方法，原则上利用此表达式可以计算任意多边形均匀带电线的空间电势和电场，提供了一个计算任意多边形均匀带电线的普遍方法，具有良好的普适性。实例计算任意四边形均匀带电线的空间电势和空间电场，并讨论了矩形、正方形及其中心轴线上的特殊情况。

[1] 张连顺,姜万禄.环形线电荷的电场分布[J].大学物理,1998,17(8):21-23.

[2] 程昌林,王慧,李业风.均匀带电细圆环的电场[J].大学物理,2003,22(6):15-17.

[3] 张之翔.电磁学中几个简单问题里的椭圆积分[J].大学物理,2002,21(4):22-24.

[4] 贾秀敏.均匀带电圆环片的空间静电场分布[J].物理与工程,2014,24(2):54-56.

[5] 张之翔.均匀带电圆环的电场强度[J].大学物理,2012,31(5):14-16.

[6] 尹妍妍,梁志强,刘进庆,等.均匀带电细圆环电场的计算机模拟[J].物理与工程,2012,22(4):33-36.

[7] 邝向军.均匀带电圆环的空间电势分布[J].江西师范大学学报,2003,27(6):697-700.

[8] 邝向军.共轴均匀带电薄圆盘间的相互作用力[J].物理与工程,2004,14(3):37-40.

[9] 邝向军.含不稳定源轴对称非静态场的计算[J].大学物理,2006,25(10):30-33.

[10] 樊雅平,黄生学.均匀带电正方形线圈的空间电场分布[J].河池学院学报,2009,29(5):25-28.

[11] 邝向军,张伟.均匀带电矩形线框的空间电场[J].宜宾学院学报,2016,16(12):88-92.

[12] 邝向军,廖旭.任意三角形均匀带电线框的空间电势和空间电场计算[J].大学物理,2016,35(9):7-11.

[13] 袁庆新,杜银霄,曾凡光.任意三角形线电荷的电场分布[J].大学物理,2013,32(8):29-32.

[14] 卢林芳,胡先权,周林,等.有限长直线电荷等电势线和电力线的求解与描绘[J].重庆师范大学学报:自然科学版,2008,25(3):66-69.

Electric Potential and Electric Field Calculations onArbitrarily Quadrilateral Uniformly Charged Coil

KUANGXiangjun,JIALianbao

(School of Science, Southwest University of Science and Technology, Mianyang 621002, China)

Using the expression of electric potential distribution for uniformly charged wire, the electric potential distribution expression for uniformly charged wire at arbitrarily space position is derived. Then, using the relation between electric potential gradient and electric field, the electric field intensity coordinate component expression for uniformly charged wire at arbitrarily space position is gotten. Introducing each vertex coordinates into the above expression accordingly, adopting the method of piecewise calculation and overlay, the electric potential and electric field of arbitrary polygon charge wire can be calculated in principle. As an example, the electric potential and electric field of arbitrarily quadrilateral charged coil are calculated, and the special cases for uniformly rectangular and square charged coil are discussed. A common method for calculating arbitrary polygon charged wire is presented which has good universality. The results of electric potential and electric field distribution is a function of spatial coordinates. It is specific, accurate, and convenient for application in engineering.

arbitrarily quadrilateral uniformly charged coil; subsection calculation; electric potential distribution; electric field distribution

2017-03-19

国家自然科学基金(11505144)

邝向军(1967-)，湖南永州人，教授，博士，主要从事凝聚态物理方面的研究，(E-mail)kuangxiangjun@163.com

1673-1549(2017)03-0079-06

10.11863/j.suse.2017.03.16

O441

A