求解需求可拆分车辆路径问题的人工蜂群算法

姜婷

(1.安徽经济管理学院信息工程系, 合肥230059;2.合肥工业大学管理学院, 合肥230009)

求解需求可拆分车辆路径问题的人工蜂群算法

姜婷1,2

(1.安徽经济管理学院信息工程系, 合肥230059;2.合肥工业大学管理学院, 合肥230009)

研究了需求可拆分的车辆路径问题(SDVRP)的基本数据模型，分析了相关解的基本特点，提出了一种改进的人工蜂群算法进行求解。首先，在不考虑车辆容量和拆分需求的前提下，求出TSP大路径；然后，对TSP大路径进行切割，在切割的地方对客户点的需求进行拆分；最后，在前述操作基础上形成初始解，采用改进人工蜂群算法进行优化。在人工蜂群阶段，三种蜜蜂在全局和邻域范围内不断优化当前解。通过仿真实验与其它算法对比，验证了提出的算法在有效性和稳定性上，具有良好的效果。

需求可拆分；车辆路径问题；人工蜂群算法；路径切割

引言

车辆路径问题(VRP)是物流运输和配送环节的重要前沿问题，但传统的VRP问题大都假设每个客户的配送需求只能由单辆车在单次服务中完成。然而，现实物流中可能出现客户需求量超过车辆的最大载重能力的情况，因此必须对客户需求进行拆分。1989年，DROR等人[1]首度提出需求可拆分车辆路径问题( Split Delivery Vehicle Routing Problem，SDVRP)。Archetti等人[2-4]证明，对客户需求进行合理拆分，会比传统VRP的解决方案减少总运输距离和派车数量，进而降低物流运作的成本。

与传统VRP一样，SDVRP的求解算法分为精确算法和近似算法。精确算法只能求解规模很小的问题，不能适应发展迅猛的物流行业中的车辆路径问题现状，因此求解SDVRP一般采用近似算法，主要是启发式算法和元启发式算法。DROR等人[5]最早提出了采用局部搜索算法解决SDVRP。其后，很多研究者采用禁忌算法求解SDVRP并取得了一定进展。Archetti等人[3]提出了简单领域搜索禁忌算法、Alemant等人[6]提出了词汇构造禁忌探索算法、Berbotto[7]提出了随机粒度禁忌搜索算法、孟凡超等[8]提出了多邻域搜索禁忌算法、熊浩等[9]提出了三阶段禁忌算法分别求解SDVRP。除此之外，也出现了其他启发式算法求解该问题的研究成果。如Boudia[10]提出的基因算法，Wilck[11]提出的遗传算法，隋露斯[12]提出的蚁群算法，刘旺盛等[13]和向婷等[14]提出的聚类算法，汪婷婷[15]、姜婷[16]等提出的蜂群优化算法(BCO)，对SDVRP的求解进行了一些有益的尝试，开拓了新的研究方向。

人工蜂群算法(Artificial Bee Colony, ABC)是群智能算法的一种，于2005年由Karaboga[17]提出，具有参数少，鲁棒性强的特点，在求解NP问题上取得了较好的效果。目前，利用ABC算法求解需求可拆分车辆路径问题的相关研究很少。本文在已有研究成果基础上，将离散人工蜂群算法与SDVRP的特征相结合，探索构造了一种先求解再分组的算法，得到SDVRP的近似最优解。

1SDVRP的数学模型

为简化问题及便于进行算法效果比较，本文设定的研究对象为单车场、单车型、没有时间窗限制、纯装货(或纯卸货)的SDVRP，采用大多文献通用的模型进行研究。具体描述如下：有n个客户，由同一车场最大载重量为W的多辆车进行服务，每个客户的需求可以被一辆或者多辆车满足，求解当总行驶距离最短时每个车辆的行驶路径。

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

其中，式(1)是SDVRP的目标函数，即要求总线路距离最短；式(2)表示进入某点总的车辆数与离开某点总的车辆数相等；式(3)表示每个客户至少被访问一次；式(4)表示线路中的子回路被消除；式(5)表示表示每辆车装载的总量不能超过其运载能力上限；式(6)表示当车辆访问某客户点时该客户才能被服务；式(7)表示客户点需求被完全满足；式(8)表示每条线路满足客户需求量不会超过客户需求的总量。

2求解SDVRP的人工蜂群算法

人工蜂群算法是模拟蜜蜂的采蜜行为提出的算法，将求解问题的目标具体化为个体适应度值进行求解。雇佣蜂、观察蜂和侦查蜂在全局和邻域范围内搜索优质蜜源，通过不断迭代，以适应度高的解不断替代适应度低的解，逐步提高解的质量，直到达到结束条件。

本文求解SDVRP的基本思路是：首先按旅行商问题(Traveling Salesman Problem，TSP)进行求解，构造一个大TSP解。然后以车辆容量为标准对该解进行切割和拆分，寻找最优切割方案使总路径长度最低，得到最优近似解。其中，大TSP解指的是在不考虑车辆容量限制和客户点需求拆分的前提下，包括车场和顾客所有节点的TSP路线组合。如1个车场8个客户点的某个大TSP解是0-1-3-6-2-5-4-7-8-0，切割后的解是0-1-3-6-2-0-5-4-7-8-0。可以看出，从节点2-5的连接处进行了切割，即原本直接连接的节点2和节点5改为分别与车场相连。切割增加的成本为2-5的节约值，即节点2和节点5到车场的距离之和减去节点2至节点5的距离。

2.1解的基本分析

通过对文献[1,3,5,13]研究，假设包括客户点与车场在内所有的点与点距离关系符合三角形不等式(即两边之和大于第三边)，SDVRP的求解被证明有如下特点：

(1)如果客户需求与车辆最大运载能力相等，则该客户点的需求不应拆分。

(2) 客户点被拆分的数量小于路线的总数量。

(3) 如果问题有可行解，则经过优化的解的任意两条线路最多只会存在一个共同点。

根据第(3)点，文献[9]作了相关分析，证明子路径可以在大TSP解的基础上在共同点处进行切割得到，同时对共同点的需求进行拆分。

2.2算法步骤

本文提出的SDVRP的求解方法属于先求解再分组的类型：第一阶段不考虑车辆容量和拆分需求，求出TSP大路径；第二阶段对TSP大路径进行切割，在切割的地方对客户点的需求进行拆分，切割后形成的多条子路径满足容量限制。在此基础上形成初始解，采用人工蜂群算法进行优化。具体步骤如下：

(1) 算法初始化

设置蜂群规模SN、最大迭代次数MaxCycle、邻域最大搜索次数limit。

(2) 问题编码和形成基础结构

将车场和客户点进行编码，车场编号为0,客户编号为自然数。在此基础上，采用2-opt形成TSP大路径。为降低编码难度，该阶段不考虑车辆容量和拆分需求，只提供一个基础结构。

(3) 生成初始解

对TSP大路径进行切割，同时在切割点进行需求拆分，形成子路径。该阶段采用简单切割方法，即累加客户需求量直到达到车辆的最大容量。将不同切割方案形成的路径组合按目标函数值降序排列，取前SN个作为初始解，记为x1,x2,…,xSN。将前一半设为当前解，最优解为x1。

(4) 迭代改进

步骤1针对每一个当前解进行如下操作：将所有的客户节点按照其删除节约代价降序排列并形成序列，然后此基础上进行删除和重新插入操作，选择插入代价最小的与原解进行比较，该步骤相当于雇佣蜂的邻域搜索。如果新解的目标函数值小于原解，则代替原解，否则保持原解不变。该步骤具体过程如算法1所示。

算法1领域搜索算法

输入：当前解s

输出：新解s′

(1)从当前解s中删除客户节点i,将形成的解赋值为s′；

(2)将i重新插入到不同位置，形成序列Li；

(3)计算s′需求被全部服务的最小插入代价minf，路径设为rf；

(4)计算s′需求被部分服务的最小插入代价minp，路径设为rp，计算该路径能满足需求的前m个元素；

(5)比较minf和minp，如果前者小于等于后者，则将节点i的需求拆分并插入到路径rf中；否则将满足需求的前m个元素rp插入到路径rp中；

(6)产生并输出新解s′

步骤2将步骤1产生新解的适应度除以所有解的适应度之和得到跟随蜂的跟随概率。然后继续采用步骤1的局部搜索操作，找到适应度更高的解。

步骤3侦查蜂通过随机方式产生新解，替换掉超过limit次数未发生改变的解；

步骤4记录到目前为止适应度最高的解；

步骤5判断是否满足终止条件，如果满足则输出最优解。

3实验仿真及结果分析

为验证算法有效性，本文采用文献[13]中的数据进行测试，算法由Matlab R2013a实现，在操作系统为Win7、CPU为Intel Core i3 2.6GHZ、内存为4GB的计算机上运行。

实验数据为15个客户点的SDVRP问题，车辆的最大运载量为500，车场的坐标为原点。客户点信息见表1。

表1客户点的信息

本文取种群规模设置为60，最大迭代次数为50，搜索阈值次数为10，算法运行10次。计算采用欧几里得距离。采用本文提出的算法，10次实验结果见表2，最优路径见表3，与其他算法的比较结果见表4。

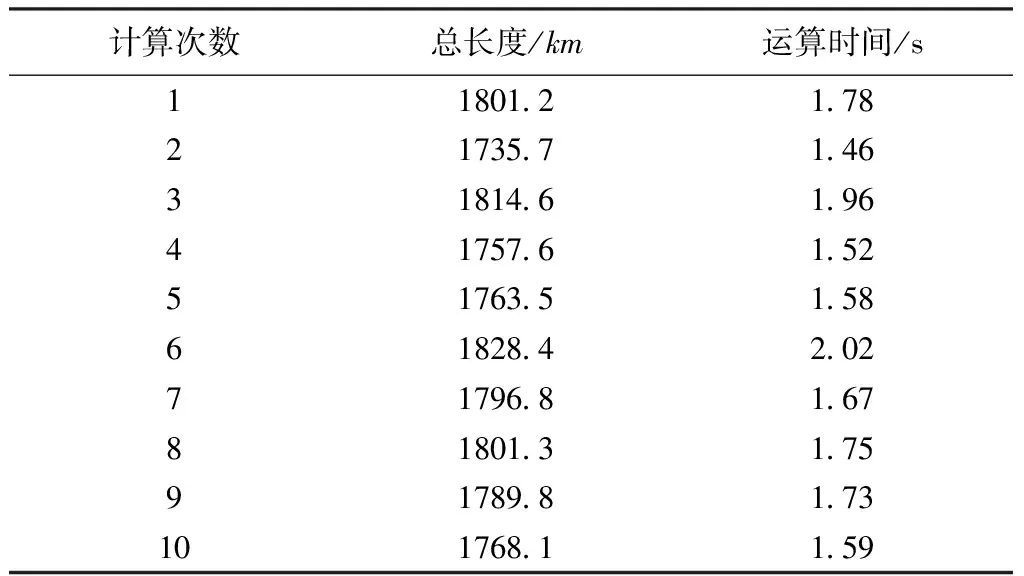
表2本文算法求解结果

表3本文算法求得最优路径

表4不同算法的最优结果

以上实验结果表明，人工蜂群算法在求解SDVRP是有效且稳定的，求解速度较快，为1～2s。最优解为1757.6 km，比传统VRP方法降低了11.68%。本文算法效果优于群智能算法之一的蚁群算法，接近并略好于聚类和BCO算法。实验表明，本文算法说明对客户需求的拆分可以缩短车辆路径，从而让降低物流成本成为可能。

4结束语

需求可拆分的车辆路径问题是对传统VRP的一定改变，客户的需求可以被不止一辆车服务，因此需求可以被拆分，这对节约车辆成本、缩短行驶路径是有益的。本文在已有研究的基础上总结了该问题求解的特点，提出了采用改进的人工蜂群进行求解。该算法首先在不考虑车辆容量限制和拆分需求的前提下使用2-OPT设计大TSP路径，然后对TSP进行切割和拆分，形成初始解。接着，通过雇佣蜂、跟随蜂、侦查蜂在全局和邻域范围内不断优化当前解，直到达到限制条件。本文算法拓宽了SDVRP求解的思路，但算法还有一定的改进空间，还需采用更多的数据案例进行测试并验证。

[1] DROR M,TRUDEAUP.Savings by split delivery routing[J].Transportation Science,1989,23(2):141-145.

[2] ARCHETTIC C,MANSINI R,SPERANZA M G.Complexity and reducibility of the skip delivery problem[J].Transportation Science,2005,39(2):182-187.

[3] ARCHETTICC,SAVELSBERGH M W,SPERANZA M G.Worst-caseanalysis for split delivery vehicle routing problems[J].Transportation Science,2006,40(2):226-234.

[4] ARCHETTIC C,FEILLET D,GENDREAU M,etal.Complexity of the VRP and SDVRP[J].Transportation Research Part C:Emerging Technologies,2011,19(5):741-750.

[5] DROR M,TRUDEAUP.Split delivery routing[J].Naval Research Logistics,1990,37(3):383-402.

[6] ALEMAN R E,HILL R R.A tabu search with vocabulary building approach for the vehicle routing problem with split demands[J].International Journal of Metaheuristics,2010,1(1):55-80.

[7] BERBOTTO L,GARCIA S,NOGALES F J.A randomized granular tabu search heuristic vehicle routing problem with for the split delivery vehiclerouting problem[J].Annals of Operations Research,2014,222(1):153-173.

[8] 孟凡超,陆志强,孙小明.需求可拆分车辆路径问题的禁忌搜索算法[J].计算机辅助工程,2010,19(1):78-83.

[9] 熊浩,鄢慧丽.需求可拆分车辆路径问题的三阶段禁忌算法[J].系统工程理论与实践,2015,35(5):1230-1235.

[10] BOUDIA M,PRINS C,REGHIOUI M.An effective memetic algorithm with population management for the split delivery vehicle routing problem[C]//Proceedings of the 4th International Workshop on Hybrid Metaheuristics(HM 2007),Dortmund,Germany,October 8-9,2007:16-30.

[11] WILCK IV J H, CAVALIER T M.A genetic algorithm for the split delivery vehicle routing problem[J].American Journal of Operations Research,2012,2(2):207-216.

[12] 隋露斯,唐加福,潘震东,等.用蚁群算法求解需求可拆分车辆路径问题[C]//2008年中国控制与决策会议论文集.沈阳:东北大学出版社,2008:997-1001.

[13] 刘旺盛,杨帆,李茂青,等.需求可拆分车辆路径问题的聚类求解算法[J].控制与决策,2012,27(4):535-541.

[14] 向婷,潘大志.求解需求可拆分车辆路径问题的聚类算法[J].计算机应用,2016,36(11):3141-3145.

[15] 汪婷婷,倪郁东,何文玲.需求可拆分车辆路径问题的蜂群优化算法[J].合肥工业大学学报:自然科学版,2014,37(8):1015-1018,1024.

[16] 姜婷.求解配送中心选址的改进人工蜂群算法[J].四川理工学院学报:自然科学版,2016,29(1):24-28.[17] KARABOGA D.An idea based on honey bee swarm for numerical optimization[R].Kayseri:Computer Engineering Department,EngineeringFaculty,Eroiyes University,2005.

Artificial Bee Colony Algorithm for Split Delivery Vehicle Routing Problem

JIANGTing1,2

(1.Department of Information Engineering, Anhui Economic Management College, Hefei 230059, China;2.School of Management, Hefei University of Technology, Hefei 230009, China)

Basic data model of split delivery vehicle routing problem (SDVRP) is studied. Based on the analysis of the basic characteristics of the related solutions, an improved artificial bee colony algorithm is proposed to solve the problem. First,the big TSP path is sought out in the premise without considering the capacity of the vehicle and the requirements of split. Second,the big TSP path is split, meanwhile the customer's needs is cut. Finally,the initial solution is formed on the basis of the above operations.In the phase of artificial bee colony, the current solution is continuously optimized by three kinds of bees in the global scale and neighborhood. Compared with other algorithms, the simulation results show that the proposed algorithm is effective and stable.

split delivery vehicle routing problem; vehicle routing problem; artificial bee colony algorithm; path cut

2017-04-19

国家自然科学基金项目(71271071);安徽省哲学社科规划项目(AHSKY2015D71);安徽省社科创新发展研究课题(A2015020)

姜 婷(1976-),女,安徽滁州人,副教授,博士生,主要从事决策支持系统、群体智能方面的研究,(E-mail)744583170@qq.com

1673-1549(2017)03-0006-04

10.11863/j.suse.2017.03.02

TP391

A