三次样条插值对人工神经网络预测软土固结精确度的影响

王彦之， 王天剑

(1.中南大学地球科学与信息物理学院， 长沙410083；2.贵州财经大学仿真重点实验室， 贵阳550004)

三次样条插值对人工神经网络预测软土固结精确度的影响

王彦之1， 王天剑2

(1.中南大学地球科学与信息物理学院， 长沙410083；2.贵州财经大学仿真重点实验室， 贵阳550004)

软土固结会引起漫长的地基沉降。人工神经网络(ANN)是预测地基沉降的一种常用工具。为了进行预测，需要使用一定的前期沉降观测数据训练ANN。采用两类训练方法：一类是直接使用观测数据训练网络，这是普通方法；一类是在观测数据中借助三次样条插值(CSI)技术进行等时距插值，然后一并利用观测数据和插值训练网络。三次样条插值是通过求解三弯矩方程组，在曲线的非连续数据点之间形成填充数据的技术。借助MatLab的函数Spline，可以完成插值计算过程。结果发现，在不同固结阶段进行预测，引入CSI插值训练的网络预测准确度均高于直接用观测数据训练的网络。这一发现，对于工程实践具有重要意义。

人工神经网络；三次样条插值；固结沉降；精确度；预测

引言

软土乃孔隙比较大、含水量高、可压缩性较高、强度和承载力较低、沉降量较大的软弱土层。按孔隙比，软土可分为软粘性土、淤泥质土、淤泥等。按照成因，软土可分为丘陵谷地相沉积、湖相沉积、三角洲相沉积、泻湖相沉积、滨海相沉积、溺谷相沉积、河漫滩相沉积等不同类型[1]。软土对工程的消极影响主要源于沉降。一般认为，存在三种类型沉降(三个阶段沉降)：瞬时沉降、固结沉降和次固结沉降。由于沉积形成条件的差异，不同区域、不同空间位置的软土特性各异，施工后发生的沉降规律差别很大，预测沉降也因此成了一个重要研究课题[2]。

软土地基沉降预测方法较多，主要包括基于土力学原理的经典方法，基于本构理论的计算方法，以及依托经验数据的推算方法。其中依托经验数据的推算方法又包括指数曲线法、双曲线法、有限元法、多元非线性相关分析法，以及人工神经网络方法等。

人工神经网络(简称“神经网络”)是一种在生物神经网络工作原理启示下构建的一种计算模型。不少研究表明，它可以成功地用于软土沉降或相关参数的预测。Li S L[3]利用软土地基沉降观测数据，借助MatLab仿真，成功地建立了一个BP神经网络沉降预测模型。利用类似方法，Jia L G[4]建立了一个露天采矿影响下附近地表沉降的神经网络预测模型。基于有限元分析结果，Azadi M[5]利用人工神经网络，建立了一个包含多相关变量的方程式，用于预测隧道施工期间附近建筑物沉降。利用三轴试验结果，Liu Y J[6]通过额外的动量因子、自适应学习速率和贝叶斯正则化性能函数，改进普通神经网络，发现经过处理的网络用于软土地基沉降预测时，计算速度更快，精确度更高，泛化能力更强。Ocak I[7]收集了18种不同参数(含土压平衡盾构机操作因素、隧道几何特性，地面特征等)。经过预处理，从中筛选出了最有效的成分，用于表层软土沉降预测。预测方法有三种：人工神经网络，支持向量机，以及高斯过程。结果显示，三种方法均优于当时的其他相关预测技术，能将错误率大幅度降低。根据对水泥土桩复合地基的室内试验结果，Huo T R[8]等利用水泥混合比例、置换率、循环应力比、循环次数等变量，预测复合地基的永久沉降，发现神经网络模型比多元线性回归模型具有更好的预测和泛化功能。

也有研究者用神经网络预测压缩指数和再压缩指数，因为它们是计算细粒土固结沉降的重要参数，而且通过室内压缩仪测得这些参数相对耗时。Moayed R Z[9]使用经遗传算法优化的神经网络，依据初始空隙率，液限和比重的三个变量，预测压缩指数和再压缩指数。根据从伊朗Mazandaran省多个地点收集的300个数据训练网络和测试的结果，研究者发现空隙率和液限分别是对压缩指数和再压缩指数最具影响的因素，比重变化对两个指数同时具有显著影响。Kurnaz T E[10]用神经网络研究的结果与此稍有分歧，发现初始空隙率、液限和塑性指数等虽对压缩指数的预测比较成功，但对再压缩指数的预测不太理想。Oda K[11]利用神经网络和蒙特卡洛模拟技术，估计了某机场全新世软土的特性。结果显示，神经网络对孔隙比以及固结压力和空隙比关系的估计精确度，高于其对压缩指数和先期固结压力估计的精确度，利用孔隙比和固结压力对沉降的预测，比利用压缩指数和先期固结压力的预测更为准确。

在中国CNKI数据库，用“固结”、“沉降”、“神经网络”为线索检索，可以发现64条记录(2016年12月3日检索)。这些研究大都通过实例验证了神经网络的应用价值，这里不再赘述。

上述研究中，有些学者侧重于探索神经网络优化技术，有些聚焦于神经网络与其他平行技术的比较。预测的对象不仅包括软土固结沉降本身，也包括可用于沉降计算的参数及其关系等。部分研究发现存在一定的分歧，这可能与研究程序、土质特性等因素有关。这些研究从不同方面考查了神经网络的功能。但是，既往相关文献很少涉及插值预测技术。为了进行有效预测，一般需要充足的数据训练神经网络，而实践中可能会存在数据不足，或者数据分布不均衡等现象，这就需要用到插值技术弥补。本研究将通过实例，着重考查三次样条插值技术对优化BP神经网络的功效。

1人工神经网络和三次样条插值的原理

1.1人工神经网络

人工神经网络是基于大脑加工信息的启示，构建的一种计算模型。人工神经网络有不同类型，如感知器网络、线性神经网络、BP神经网络、反馈神经网络、径向基神经网络、自组织竞争网络、随机神经网络等。不同网络结构各异，工程领域常用的BP神经网络模型如图1所示。

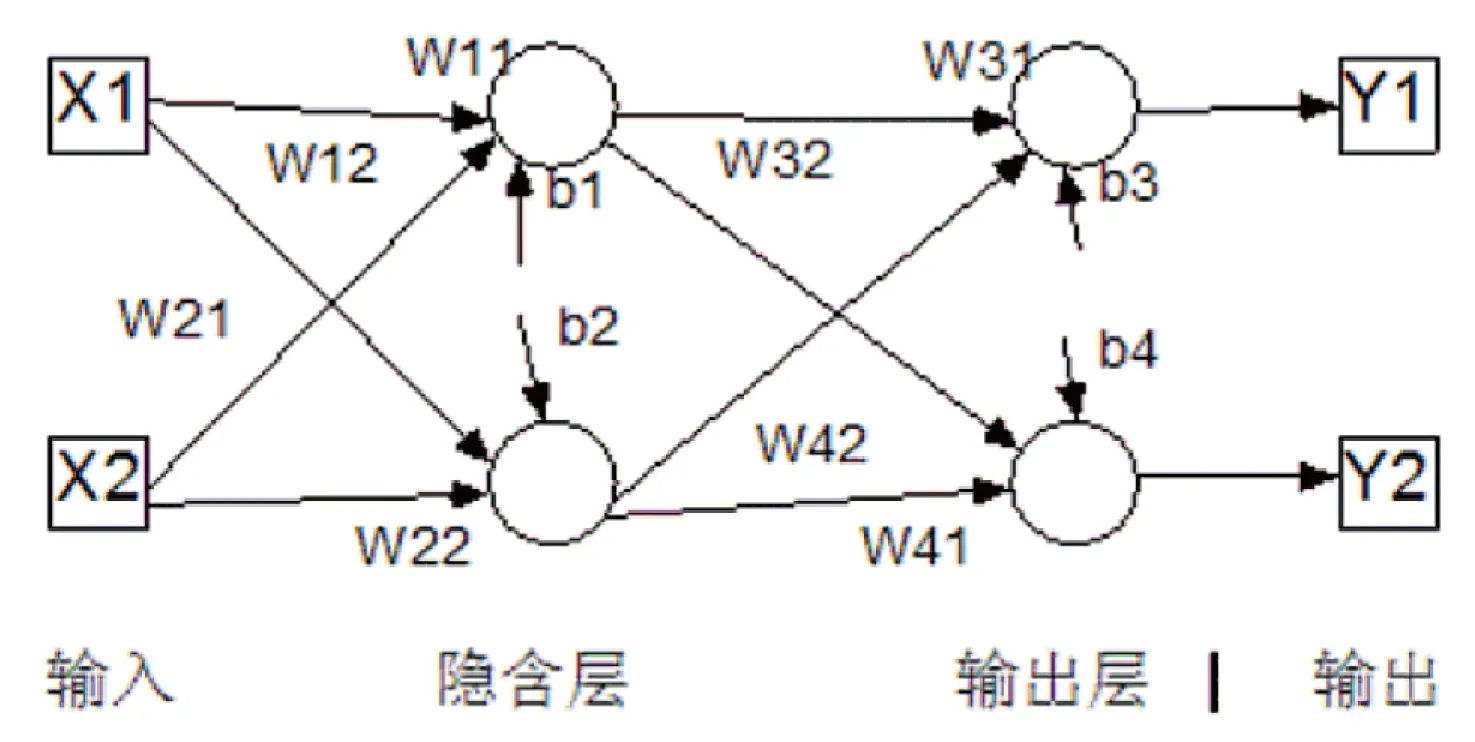
图1BP人工神经网络模型简图

图1中X1和X2代表输入的二维向量(相当于神经刺激)，圆圈代表神经元(相当于细胞核)，Y1和Y2代表输出的两个向量(或标量)(相当于神经网络的反应)。箭头代表影响，W代表影响权重，b代表偏值(是对输入的调剂变量，相当于回归方程中的常数项)。每一个神经元接收到的输入总量是：

(1)

即输入总量为各个输入乘以其权重，然后求和，外加一个偏值。每一个神经元向后层传递影响时，其数值将再次通过一个传递函数进行。

不同神经网络采用的传输函数可能不同。BP人工神经网络一般采用Sigmoid或者线性函数作为传递函数。Sigmoid又分为Log-Sigmoid(式2)和Tan-Sigmoid(式3)：

(2)

(3)

采用Log-Sigmoid，函数值介于0到1之间，采用Tan-Sigmoid，函数值介于1到-1之间。输出层向后传递输出时，一般采用线性函数，因为若采用Sigmoid函数，结果输出会被压缩在0到1或者1到-1范围内。

BP人工神经网络的输入和输出可以是1维，也可以是多维；隐含层从1层到多层不等；从输入、隐含层到输出层，BP人工神经网络中前面的信息可以跨层后传。

1.2三次样条插值

工程师制图过程中，会把富有弹性的细木条(“样条”)用铁钉固定于样点之上，在其他地方使其随意弯曲，此后沿该木条勾画曲线，即“样条曲线”。三次样条插值是借助数学方法(求解三弯矩方程组)，在样点之间形成填充数据，以获得平画曲线的方法。其数学定义是：如果函数S(x)∈C2[a,b]，在区间[a,b]中存在数据节点a=x0

(4)

其中，I=0,1,…n-1。令

di=6f[xi-1,xi,xi + 1]

可得

(5)

矩阵(5)求解，代入式(4)，便可得到每一个亚区间内三次样条插值的表达式[12-13]。在实际应用中，可利用MATLAB软件的spline函数，完成上述复杂计算。

2实例分析

2.1数据资料与分析目的

表1是某工程沉降过程原始数据[14-15]。本研究将利用神经网络，依据测量时间预测对应的沉降量。为了检验三次样条插值的功效，将在不同预测条件下，同时对比插值处理数据训练的网络，与非插值处理数据训练的网络，在预测中的准确度和错误率。

表1不同时间观测到的沉降量

注：固结度 = (特定时间的沉降量 / 最终沉降量)× 100%，其中最终沉降为244 mm。

2.2分析程序

(1)构建神经网络模型程序。本研究采用newff函数创建神经网络模型。因输入和输出均为一维向量，采用包含一个隐含层的网络即可满足需要。具体程序如下：

x=[…]; %用于网络训练的观测时间

y=[…]; %用于网络训练的沉降数据

xp=[…]; %用于仿真预测的时间

rand('seed',2); %网络运算初始随机数种子

net=newff(x,y,[n]); %网络模型

net=train(net,x,y); %网络训练指令

yp=sim(net,xp);%沉降仿真预测指令

(2)选择和处理网络训练数据。本研究将分别利用固结达到36%、82%和91%对应的数据进行网络训练。在每一种条件下，分别采用原始数据和经过三次样条插值处理过的数据进行网络训练。插值的频率为每隔10天插入一个数据。例如：

若利用原始数据训练时采用的是：

x = [0 29 64…]

y = [0 14 18…]

则利用三次样条插值处理后的数据训练时采用的将是(插值借助MatLab自带函数工具计算)：

x=[0 10 20 29 30 40 50 60 64…]

y=[0 7.4917 11.9036 14 14.1539 15.1610 15.8430 17.1182 18…]

(3)训练网络并进行仿真预测检验。

2.3分析结果

2.3.1利用36%固结度之前的数据预测

(1)网络模型

根据表1，第154天观测沉降为88 mm，固结度达到36%。此前共6组数据。预测时采用的网络模型含有一个输入(x向量)，一个隐含层(1个神经元)，一个输出层，以及一个输出向量(y)。

(2)预测结果

图2是预测结果，横轴为时间，纵轴为沉降量(垂线之前为训练数据曲线，垂线之后为预测数据曲线)。带“o”曲线对应于实际沉降，带“*”曲线对应于6组原始数据训练网络后预测的沉降，带“Δ”曲线对应于6组原始数据加上三次样条插值训练网络后预测的沉降。

图2原始数据预测、插值处理数据预测与实测(36%固结之后的沉降)

根据图2可知，利用36%固结度之前的纯原始数据训练网络，结果没有意义。第154天的沉降量是88 mm，向后预测出的沉降值(mm)依次是：72.6900，72.7366，72.7403，72.7409，72.7410，72.7410…。出现这种现象的原因是原始数据较少，对曲线走向没有约束力。曲线震荡较大，走向没有规律。从88 mm跌落到72.6900 mm之后，虽然有回

升趋势，但幅度极其微小，粗略看就是一条直线(讨论部分有更多介绍)。利用经过插值处理的数据训练网络，误差虽然较大，但比前者几乎减半，且没有出现明显的跌宕，收敛过程基本合理。

2.3.2利用82%固结度之前的数据预测

(1)网络模型

根据表1，第244天观测沉降为199 mm，固结度达到82%。此前共8组数据。预测时采用的网络模型与“3.3.1”相同。

(2)预测结果

结果如图3所示(垂线之前为训练数据曲线，垂线之后为预测曲线)。原始数据和经过插值处理的数据训练的网络，预测结果都很接近观测值。

图3原始数据预测、插值处理数据预测与 实测(82%固结)

为了考查细微差别，将原始数据训练的网络与经过插值处理数据训练的网络预测的数值，与实测数据进行对比，并计算各自平均误差和错误率。结果见表2。

表2实测、原始数据预测与插值处理数据预测结果(82%固结)

注：错误率=平均误差/实测均值×100%

根据表2，原始数据训练的网络平均误差12.9 mm，错误率5.5%。经过插值处理的数据训练的网络，平均误差9.3 mm，错误率3.9%。可见插值处理对BP网络具有优化作用。

2.3.3利用91%固结度之前的数据预测

(1)网络模型

根据表1，第313天观测的沉降量221 mm，对应于91%固结度。此前共10组数据。由于数据增多，隐含层一个神经元的模型已经明显不适应，需要改为隐含层6个神经元的模型。其原因是，数据越多，需要拟合的关系越复杂，用到的调剂变量越多。每一个神经元相当于一个调剂变量，用于调整模型与数据的关系。

(2)预测结果

结果如图4所示(垂线之前为训练数据曲线，垂线之后为预测曲线)。原始数据和经过插值处理的数据训练的网络，预测曲线与观测曲线基本吻合，即预测结果和观测值基本一致。

图4原始数据预测、插值处理数据预测与 实测(91%固结)

为了考查细微差别，将原始数据训练的网络与经过插值处理数据训练的网络预测的数值，与实测数据进行对比，并计算各自平均误差和错误率。结果见表3。

表3实测、原始数据预测与插值处理数据

根据表3，原始数据训练的网络平均误差9.1 mm，错误率3.9%。经过插值处理的数据训练的网络，平均误差3.1 mm，错误率1.3%。插值处理数据训练的网络优于原始数据训练的网络。

3讨论

本研究考查了神经网络对软土地基沉降的预测效果。分别以36%、82%和91%固结度对应时间之前的数据为依托，对比了采取原始数据预测和插值处理数据预测的异同。结果表明，插值处理数据训练的网络在各种条件下都优于原始数据训练的网络。这可以通过图5予以解释。

图5神经网络拟合曲线在训练数据点间的波动

图5中的横轴代表预测条件，纵轴代表预测目标。神经网络在拟合曲线时，并不是按平滑走向进行的，数据点之间可能存在种种波动。训练网络时，尽管可以让曲线覆盖所有训练数据，但数据点越少，点与点之间波动的可能性越大，训练出来的网络在预测应用时，出错的可能性越大。这就是所谓的“局部适配”，泛化不足现象。通过三次样条插值，插入的数据是按平滑走向分布的。这些数据点，对拟合曲线会产生“约束”作用，减少其波动机会。因此插值训练的网络，拟合出的曲线走向更有规律性，更能预测如地基沉降之类的规律性变化。

4结论

本研究介绍了神经网络的基本结构，通过实例，在不同条件下检验了三次样条插值的预测功效，结论如下：

(1)神经网络模型用于预测软土地基固结沉降时，训练的数据越多，网络预测越准确。

(2)训练网络的数据覆盖完成82%固结度对应时间区间时，网络预测可以达到较高准确度。

(3)经三次样条插值处理的数据训练的网络，比未经处理的数据训练的网络预测精确度更高。

(4)随着训练数据规模的增加，网络隐含层神经元数目可能需要进行一定的调整。

本研究对工程实践具有重要意义，因为它可以使有限的预测条件，发挥更大的预测价值。由于数据有限，本研究所得结论有待更大样本检验。

[1] 董康.软土地基的力学特性及其处治方法[J].山西建筑,2014(23):108-110.

[2] 张帆.某运营高速公路软基区路基开裂监测及其成因分析[J].四川理工学院学报:自然科学版,2017,30(1):79-83.

[3] LI S L,HE S Y,WANG X T,et al.Prediction of soft ground settlement by BP neural network[J].Applied Mechanics & Materials,2014,608-609:825-828.

[4] JIA L G,SUN K H.Neural network prediction of ground surface settlement under the influence of open pit mining[J].Advanced Materials Research,2014,1073-1076:2128-2134.

[5] AZADI M,POURAKBAR S,KASHFI A.Assessment of optimum settlement of structure adjacent urban tunnel by using neural network methods[J].Tunnelling & Underground Space Technology,2013,37(2):1-9.

[6] LIU Y J,LI Z M,WANG Y,et al.Study on deformation property of soft soil based on neural networks[J].Applied Mechanics & Materials,2013,353-356:270-273.

[7] OCAK I,SEKER S E.Calculation of surface settlements caused by EPBM tunneling using artificial neural network,SVM,and Gaussian processes[J].Environmental Earth Sciences,2013,70(3):1263-1276.

[8] HUO T R,BAI S G.Permanent settlement prediction of composite foundation improved by cement-soil piles under cycle loading[J].Advanced Materials Research,2012,482-484:1205-1208.

[9] MOAYED R Z,KORDNAEIJ A,MOLA-ABASI H.Compressibility indices of saturated clays by group method of data handling and genetic algorithms[J].Neural Computing & Applications,2016,25(6):1-14.[10] KURNAZ T F,DAGDEVIREN U,YILDIZ M,et al.Prediction of compressibility parameters of the soils using artificial neural network[J].Springerplus,2016,5(1):1801.[11] ODA K,YOKOTA K,Bu L D.Stochastic estimation of consolidation settlement of soft clay layer with artificial neural network[J].Japanese Geotechnical Society Special Publication,2016,74(2):2529-2534.

[12] 张凯选,马传宁.结合三次样条和时序模型的桥墩沉降预测[J].测绘科学,2016,41(12):229-232.

[13] 李谆,金鼎沸.基于三次样条插值和GM(1,1)模型的高速公路路基沉降预测[J].公路工程,2015,40(2):221-225.

[14] 顾乐民.最小一乘法在岩土地基沉降中的应用[J].岩土力学,2016,37(8):2366-2372.

[15] 朱志铎,周礼红.软土路基全过程沉降预测的 Logistic 模型应用研究[J].岩土工程学报,2009,31(6):965-969.

The Effect of Cubic Spline Interpolation on the Prediction ofSoft Soil Settlement with Artificial Neural Network

WANGYanzhi,WANGTianjian

(1.School of Geosciences and Info-Physics, Central South University, Changsha 410083, China；2.GuizhouKey Laboratory of Economics Simulation, Guizhou University of Finance and Economics, Guiyang 550004, China)

The consolidation of soft soil may cause a long-term settlement. BP artificial neural network (BP-ANN) is a general technique for the prediction of settlement. Teaching the BP-ANN with a certain amount of settlement data is indispensible for the purpose of prediction. Two types of network teaching methods are employed: one involving the use of pure measurement records, and the other involving the use of both the measurement records as well as data produced by cubic spline interpolation(CSI). CSI is a technique for producing data between recorded data interval on a curve by means of solving tridiagonal linear equation. The results show that the prediction by the latter is consistently better than the prediction with the former. The finding is of great practical significance in engineering.

settlement; prediction; artificial neural network; cubic spline interpolation

2017-04-13

国家自然科学基金项目(F030203)

王彦之(1993-)，男，河南南阳人，硕士生，主要从事地质工程方面的研究，(E-mail)821240185@qq.com； 王天剑(1968-)，男，贵州贵阳人，教授，博士，硕士生导师，主要从事网络仿真方面的研究，(E-mail)daka777@qq.com

1673-1549(2017)03-0067-06

10.11863/j.suse.2017.03.14

TU 433

A