单调有界准则的推广与级数的敛散性

杜先云， 任秋道， 文华燕， 王敏

(1.成都信息工程学院数学学院， 成都610225；2.绵阳师范学院数学与物理学院， 四川绵阳621000；3.西南科技大学城市学院， 四川绵阳621000)

杜先云1， 任秋道2， 文华燕3， 王敏2

(1.成都信息工程学院数学学院， 成都610225；2.绵阳师范学院数学与物理学院， 四川绵阳621000；3.西南科技大学城市学院， 四川绵阳621000)

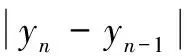
数列；数列收敛；级数收敛

引言

1单调有界准则的推广及应用

对于有界数列{yn}，如果它不单调，有如下结论：

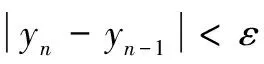
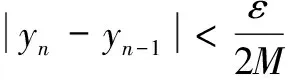
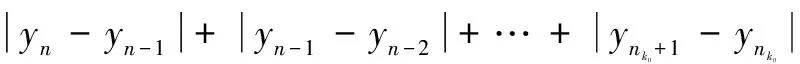
于是

因此，数列{yn}收敛。证毕。

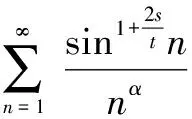
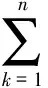
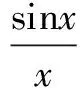
由此可见，当N∈Z+越大时，近似值越精确。

用类似的方法可以得到如下的结论：

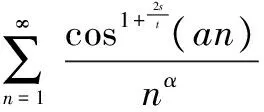
根据推论3、推论4，可得：

容易得到更一般的结论：

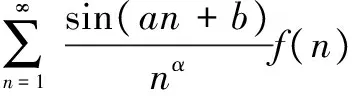
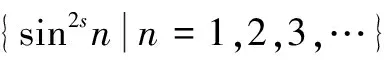
sin2snk=max{sin2s(k′+1),sin2s(k′+2),

sin2s(k′+3)，sin2s(k′+4)}0因此，下确界。从而

用同样的方法可以得到如下的结论：

证明对s进行归纳。(1)当s=1时，(a-2kπ)2+(b-2lπ)2>0,k,l∈Z，则有

根据推论5，结论成立。

(2)假设s结论成立。同样有

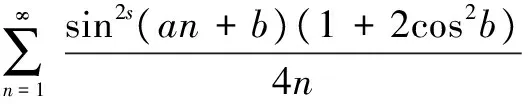
从而s+1时，结论成立。因此，结论成立。证毕。

[1] 王昆扬.数学分析[M].北京:北京师范大学出版社,2002.

[2] 陈传樟.数学分析[M].北京:高等教育版社,1983.

[3] 裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2006.

[4] 宋小迪.正项级数收敛性判别法研究[J].山东教育学院学报,1999,23(2):77-80.

[5] 杨丽.有关级数敛散性的几个问题[J].锦州师范学院学报,2003,24(2):63-64.

[6] 杜争云.压缩数列及其收敛性[J].荆楚理工学院学报:自然科学版,2010,36(7):33-36.

[7] 杨云苏,万冰蓉.一类数列收敛性的证明[J].高等数学研究,2004,12(7):34-44.

[8] 林银河.V-型函数的周期点[J].四川师范大学学报:自然科学版,2015,56(4):132-135.

[9] 杨钟玄.双比值判别法与对数判别法[J].四川师范大学学报:自然科学版,2004,47(8):57-60.

[10] 岳静.有关数列极限的几个典型例题[J].数学教学研究,2011(2):54-57.

[11] 李进,郭军.一类特殊的幂指函数极限求法[J].高等函授学报,2008(6):82-84.

[12] 冯海容,王建华.利用函数思想解决不等式“猜想”问题[J].数学教学,2008,32(10):23-25.

[13] 王远民.关于迭代生成数列的极限求法[J].商丘职业职术学院学报,2008(2):83-85.

[14] 杜先云,任秋道.如何利用构造法培养学生的创新思维[J].绵阳师范学院学报:自然科学版,2015,34(11):126-130.

[15] 杜先云,任秋道,文华燕.树的边带宽与叶子数[J].湖北民族学院学报:自然科学版,2016,34(3):1-4.

DUXianyun1,RENQiudao2,WENHuayan3,WANGMin2

(1.College of Mathematics, Chengdu University of Information Technology, Chengdu 610225, China;2.Department ofMathematics and Physics, Mianyang Normal University, Mianyang 621000, China; 3.City College,Southwest University Science and Technology, Mianyang 621000,China)

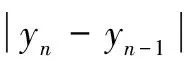
sequence; sequence convergence; series convergence

2017-03-18

四川省教育厅基金项目(16ZB0314)

杜先云(1964-)，男，四川三台人，教授，主要从事应用数学方面的研究，(E-mail)duxy2011@foxmail.com

1673-1549(2017)03-0085-04

10.11863/j.suse.2017.03.17

O186.1

A