函数列的黎曼积分的极限定理及其应用
邢家省, 杨义川, 王拥军
(1.北京航空航天大学数学与系统科学学院, 北京100191;2.数学、信息与行为教育部重点实验室, 北京100191)
函数列的黎曼积分的极限定理及其应用
邢家省1,2, 杨义川1,2, 王拥军1,2
(1.北京航空航天大学数学与系统科学学院, 北京100191;2.数学、信息与行为教育部重点实验室, 北京100191)
考虑函数列在广义积分下的极限问题,运用函数列的极限理论,在函数列的内闭一致收敛条件下和函数列的一致有界条件下,给出了黎曼可积函数列积分的极限定理的结果;在函数列的广义积分一致收敛的条件下,给出了广义积分下函数列积分的极限定理结果的充分条件,给出了广义积分下函数列积分的控制收敛定理的叙述和证明,并将这些理论方法应用于一些重要问题的解决,给出了系统的一般化理论方法,推进了理论发展和提高认识。
函数列的极限理论;广义积分;内闭一致收敛;含参变量广义积分的一致收敛;广义积分控制收敛定理
函数列积分的极限问题是分析学中的重要内容[1-16],然而,此重要问题在数学分析的经典教材中一般是没有给予充分系统的讨论,没有给出系统一般性的深刻的结果,但在数学分析的经典习题中,又出现了大量的练习题目,使人们不得不用最原始的证法去重复给出解答[6-9],没有形成一般性的理论方法。研究发现,函数列积分的极限理论完全可以在数学分析中给予系统完整的介绍,用已有的知识基础,就能得到深刻的理论结果,达到理论上应有的发展高度,并能解决大量的问题。在现有函数列的极限理论方法的基础上,充分发掘它的功能和潜力,就能得到函数列的广义积分的极限定理,使广义积分下的函数列积分的极限理论得到丰富发展,便于应用。
文献[1-16]中对函数列的积分的极限理论,从多个不同方面进行了研究,得到了一些结果,但不系统、不明确,没有发展到应有的理论高度。本文在现有研究成果的基础上,进行了系统的一般化处理,形成了一套系统的严密理论方法,丰富发展了经典理论,达到新的认识高度。
1函数列的黎曼积分的极限定理的经典结果
定理1[1-6]设{fn(x)}是[a,b]上的连续函数列,如果{fn(x)}在[a,b]上一致收敛于f(x)。则有
(1)f(x)在[a,b]上连续;
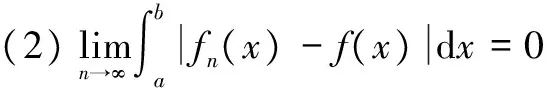

定理2[2,4,13]设{fn(x)}是[a,b]上的黎曼可积函数列,如果{fn(x)}在[a,b]上一致收敛于f(x)。则有
(1)f(x)在[a,b]上黎曼可积;
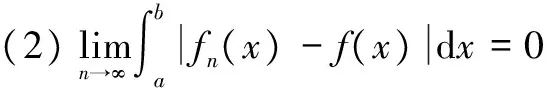

定理3[1-2,4,6]设{fn(x)}是[a,b]上的黎曼可积函数列,且满足如下条件:
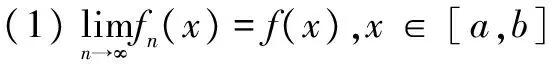
(2)存在常数M>0,使得|fn(x)|≤M,对x∈[a,b],n=1,2,…;
(3)对任意a 定理4[2,4,6]设函数列{fn}的每一项都在区间[a,b]上黎曼可积,且满足如下条件: 定理3的结论在数学分析的经典教材[1-6]中是不曾明确写出的,这样导致对大量习题[1-9]不得不用原始办法去解答,对这些习题如果套用定理3的结果就能非常简单的解决。定理3的表述方式和证明方法,具有一般性的理论意义。 如果满足条件: (1)对任意a 由定理5的叙述和证明过程可以发现,定理5中的区间[a,b)可为有限区间,也可以是无限区间,即b可为有限,或为+∞。类似地,可得: 如果满足条件: (1)对任意a 定理6的积分下限a可为有限,也可以是-∞。 (1)对任意a 定理7中的区间(a,b)可为有限区间,也可为无限区间。 如果满足条件: (1)对任意B>A>a,{fn(x)}在[A,B]上一致收敛于f(x),即{fn(x)}在(a,+∞)上内闭一致收敛于f(x); 注意定理8中的积分下限a可以为有限的,a也可以是-∞。 如果满足条件: (1)对任意B>A>a,{fn(x)}在[A,B]上一致收敛于f(x),即{fn(x)}在(a,+∞)上内闭一致收敛于f(x); 定理7和定理8常被使用的情形是控制收敛定理。 如果满足条件: (1)对任意a 定理10中的区间(a,b)可为有限区间,也可为无限区间。 如果满足条件: (1)对任意B>A>a,{fn(x)}在[A,B]上一致收敛于f(x); 定理5~定理11虽然是以函数列的极限形式叙述的,但完全可以写出其它极限过程的相应结论[3-4,8-9]。 定理7~定理11中条件的叙述方式,来源于文献[4,6]中的启发,现有文献中是不曾给出明确表述的,这里给出了具体明确的表述方式。 于是 故 例1的结果在文献[6,9]中是用原始的证法给出的,这里直接套用了函数列积分的极限定理的结果,方法上具有一般性。 例2的结果在文献[6-9]中是用原始的证法给出的,并在历史上多次作为考试题目。这里直接套用了函数列积分的控制收敛定理,给出了简便解决办法。 记 对任意A>0,{fn(x)}在[0,A]上一致收敛于f(0)φ(x),利用函数列广义积分的控制收敛定理,得 例5设φ(x)在(-∞,+∞)上连续且有界,f(x,t)在(-∞,+∞)×[0,T]上连续且有界,令 证明由于 显然右端的两个积分是一致收敛的,且被积函数是连续的,应用一致收敛的含参变量积分的连续性定理[1-5]或者函数列积分的控制收敛定理,可得 本文给出的函数列积分的极限理论方法和解决问题的过程,可以将文献[1-9]中涉及的函数列积分的极限问题,给予系统的一般化的简化处理,而不必每次按照原始方式重复给出[6-9]。新的理论结果方便于应用,达到新的认识高度,推进了理论发展和完善。 [1] 菲赫金哥尔茨.微积分学教程(第二卷)[M].8版.北京:高等教育出版社,2006. [2] 卓里奇.数学分析(第二卷)[M].4版.北京:高等教育出版社,2006. [3] 裴礼文.数学分析中的典型问题与方法[M].2版.北京:高等教育出版社,2009. [4] 汪林.数学分析中的问题研究和反例[M].北京:高等教育出版社,2015. [5] 匡继昌.Dirichlet积分九种解法的思路分析[J].高等数学研究,2012,15(4):61-64. [6] 匡继昌.实分析与泛函分析(续论)(上册)[M].北京:高等教育出版社,2015. [7] 匡继昌.实分析与泛函分析(续论)(下册)[M].北京:高等教育出版社,2015. [8] 邢家省,杨小远,白璐.两无穷区间上积分交换次序充分条件的改进及其应用[J].四川理工学院学报:自然科学版,2016,29(1):87-92. [9] 邢家省,杨小远.广义菲涅尔积分的积分交换次序计算方法[J].四川理工学院学报:自然科学版,2016,29(3):85-92. [10] 邢家省,杨小远,白璐.菲涅尔积分计算中的一致收敛性的证明方法[J].吉首大学学报:自然科学版,2016,37(5):1-9. [11] 邢家省,杨义川,王拥军.菲涅尔积分的几种计算方法[J].四川理工学院学报:自然科学版,2016,29(5):88-96. [12] 邢家省,杨义川,王拥军.函数列的广义积分的极限定理及其应用[J].吉首大学学报:自然科学版,2016,37(6):1-9. [13] 许宁.Dirichlet积分及其应用[J].高等数学研究,2014,17(3):15-19. [14] 许宁.级数求和的复分析方法[J].南京师大学报:自然科学版,2014,37(4):20-27. [15] 吴崇试.计算含三角函数无穷积分的新方法[J].大学物理,2011,30(2):53-57. [16] 邢家省,张愿章.函数列的黎曼积分极限定理的应用[J].高等数学研究,2010,13(6):50-53. Limit Theorem and Application of Functional Sequence’s Riemann-integral XINGJiasheng1,2,YANGYichuan1,2,WANGYongjun1,2 (1.School of Mathematics, Beihang University, Beijing 100191,China;2.LMIB of the Ministry of Education,Beihang University, Beijing 100191,China) Considering the functional sequence’s limit problems of generalized integral and using the limit theorem of functional sequence, for the functional sequence with uniform sector and local uniform convergence, the limit theorem for the Riemann-integral functional sequence is given. For the generalized integral of functional sequence with uniform convergence, the limit theorem for the integral functional sequence is given. And the integral dominated convergence theorem is also given. By applying all the results into solving some problems, systematical and general theory methods are proposed. limit theorem of functional sequences; generalized integral; uniform convergence; uniform convergence of generalized integral with parameter; generalized integral dominated convergence theorem 2017-02-16 国家自然科学基金资助项目(11271040);北京航空航天大学校级重大教改项目(201403) 邢家省(1964-),男,河南泌阳人,副教授,博士,主要从事偏微分方程、微分几何方面的研究,(E-mail)xjsh@buaa.edu.cn; 杨义川(1970-),男,甘肃天水人,教授,博士,主要从事逻辑代数、序代数、软计算及其应用方面的研究,(E-mail)ycyang@buaa.edu.cn 1673-1549(2017)03-0073-06 10.11863/j.suse.2017.03.15 O177.2 A



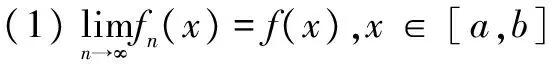


2函数列的广义积分的极限定理的几种形式










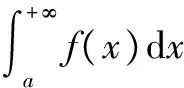

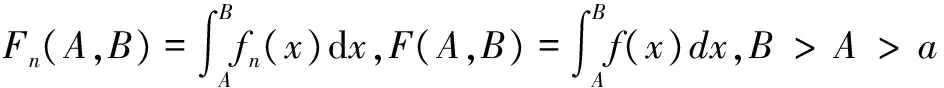
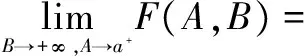



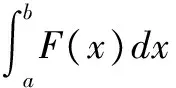

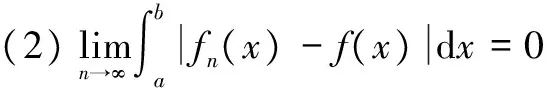
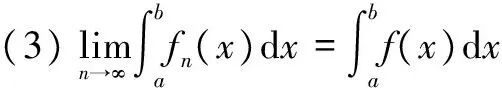

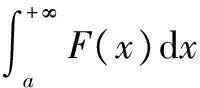



3函数列广义积分的极限定理的应用举例


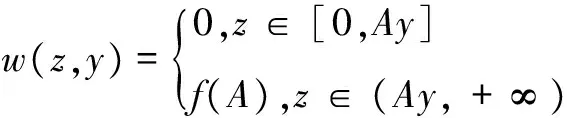











4结束语

