一道希腊阿基米德竞赛不等式试题的加强推广
2017-06-28 15:47:14福建省福清第三中学350315
中学数学研究(江西) 2017年6期
福建省福清第三中学 (350315) 何 灯
一道希腊阿基米德竞赛不等式试题的加强推广
福建省福清第三中学 (350315)
何 灯
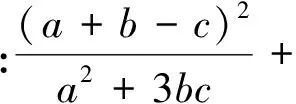
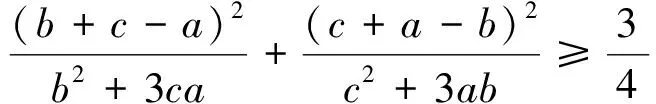
这是2017年希腊阿基米德数学竞赛试题中的一道,本文拟给出上述不等式的一个加强推广.
结论 设a,b,c>0,0≤λ≤3,则有
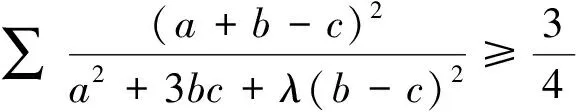
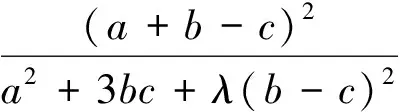
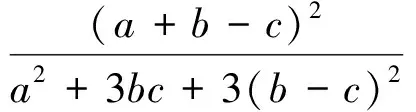
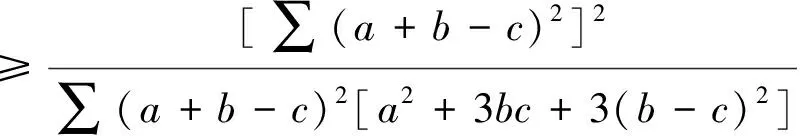
注意到3∑a4+3∑a2b2-6∑a3b
=3a2∑(a2-2ab+b2),(2)
24∑a2b2-12∑a3b-12∑ab3
=-12ab∑(a2-2ab+b2),(3)
27∑b4+27∑a2b2-54∑ab3
=27b2∑(a2-2ab+b2),(4)
2∑a2b2-2abc∑a=∑b2c2+∑c2a2-2abc∑c=c2∑(a2-2ab+b2),(5)
将式(2)-(5)左右两边分别相加,可得30∑a4+56∑a2b2-18∑a3b-66∑ab3-2abc∑a=(3a2-12ab+27b2+c2)∑(a-b)2,由基本不等式得

猜你喜欢
哈尔滨商业大学学报(自然科学版)(2022年4期)2022-08-18 13:07:30
中学生数理化·八年级物理人教版(2022年5期)2022-06-05 06:57:44
中学生数理化·八年级物理人教版(2021年5期)2021-11-22 07:57:48
中学生数理化·八年级物理人教版(2021年5期)2021-11-22 07:57:46
吉林大学学报(理学版)(2020年3期)2020-05-29 06:31:40
三峡大学学报(自然科学版)(2019年5期)2019-10-17 02:24:22
中学数学研究(江西)(2019年6期)2019-07-08 10:47:04
海峡姐妹(2019年6期)2019-06-26 00:52:32
中学生数理化·八年级物理人教版(2017年5期)2017-11-13 03:12:24
海峡姐妹(2017年4期)2017-05-04 04:03:52

