用基本不等式巧证2017年数学奥林匹克试题

江西省南昌市第十四中学 (330003) 吴倩倩

用基本不等式巧证2017年数学奥林匹克试题

江西省南昌市第十四中学 (330003)
吴倩倩

本文旨在给出2017年国际数学奥林匹克不等式题的巧妙且通俗的证明，供老师和同学学习和参考.

例1 (2017年土耳其数学奥林匹克)已知a,b,c是满足a+b+c=3的正数，求证：a3b+b3c+c3a+9≥4(ab+bc+ca).

证明：由均值不等式可得a3b+b3c+c3a+9=a3b+b3c+c3a+(a+b+c)2=(a3b+b2)+(b3c+c2)+(c3a+a2)+2(ab+bc+ca)≥4(ab+bc+ca).

注1：此题证明的关键是大方向明确，依序进行.

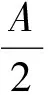
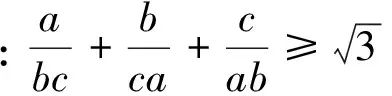
注3：合理分析，步调一致.

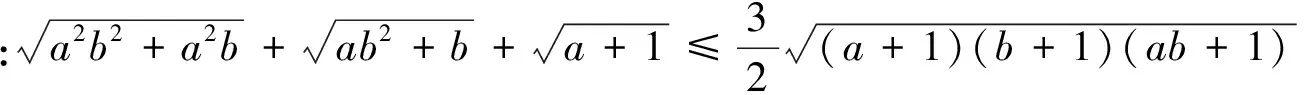
证明：由均值不等式可得

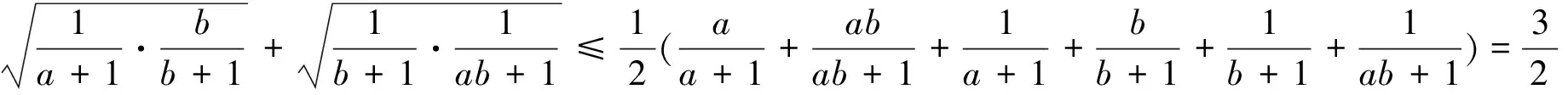
注4：还是恒等变形唱主角.

例5 (2017年摩尔多瓦数学奥林匹克)

已知n是正整数，求证：

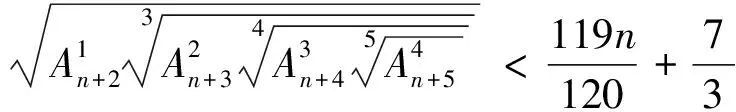
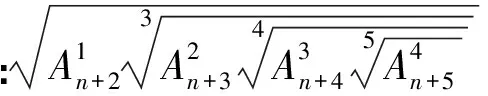
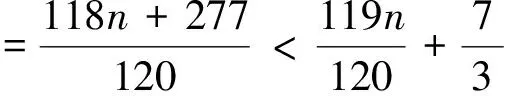
注5：做题得细心,而且要有耐心.

例6 (2017年IMO中国国家队选拔考试三试题1)已知x1,x2,…,xn(n≥4)是满足x1+x2+…+xn=1的非负实数，求x1x2x3+x2x3x4+…+xnx1x2的最大值.

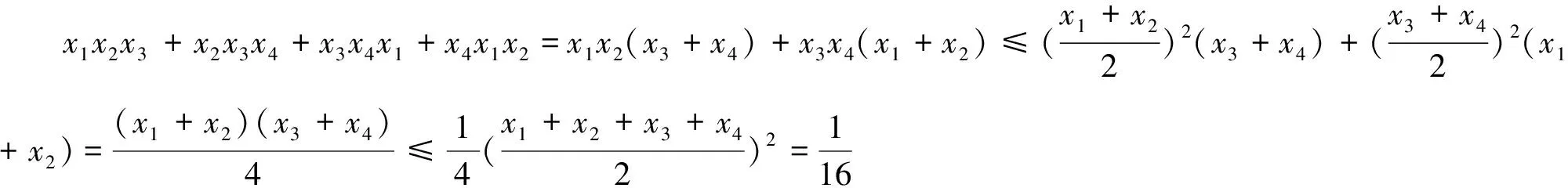
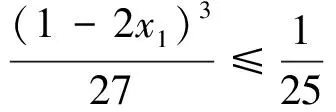
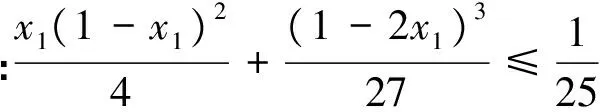
注6：题目虽然难，但是证明的工具只是基本不等式.