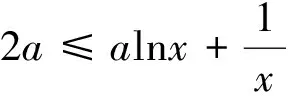重视导数题的审题减少思维定势

江苏省启东市汇龙中学 (226200) 殷春华

重视导数题的审题减少思维定势

江苏省启东市汇龙中学 (226200)
殷春华

导数是高考的必考内容之一，经过高三几轮复习，教师与学生都非常重视.很多学生慢慢形成思维定式，因而失去对导数题应有的思考.拿到函数题，学生就会一味的求导，有时反而失去简单的思路.下面仅从两个函数问题着手，分析审题、注重转化，简化解题.希望能让遇到导数题就求导的学生，有所感悟.

例1 已知函数f(x)=(x+1)lnx-x+1.

(1)若xf′(x)≤x2+ax+1对任意x∈(0,+∞)恒成立，求实数a的取值范围；

(2)求证：(x-1)f(x)≥0.

此处，解得函数y=lnx-x的最大值为-1.由最大值的定义可知lnx-x≤-1，即lnx-x+1≤0.

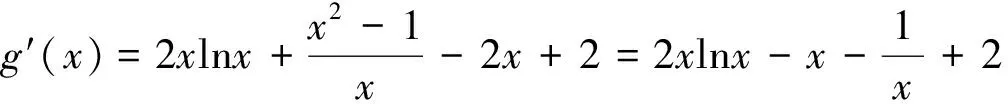
如果直接构造函数求导不易处理，应该分析题意，认真审题，换位思考，要证明不等式(x-1)f(x)≥0，只需证明x-1与f(x)的符号相同.由函数f(x)的定义域可知x>0.所以，只需对x与1进行讨论.

法一：①当0

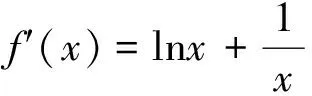
②当x=1时，显然(x-1)f(x)=0；

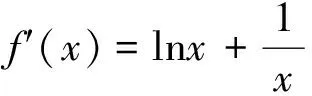
综上，不等式(x-1)f(x)≥0成立.

法二：①当0

②当x=1时，显然(x-1)f(x)=0；

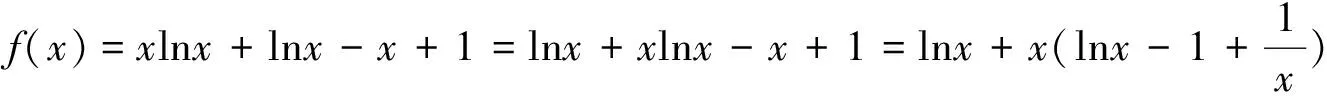
综上,不等式(x-1)f(x)≥0成立.

评析：法二利用(1)中解题过程中的结论，避开二次求导，使得问题容易解决.因此，在具体解题时，不能固于定式，要认真观察，有时题目中的(1)(2)是相互联系的，因而有时用(1)的结论解也许思路更简单.

(1)求函数f(x)的单调区间和极值；

(2)若对∀x>0，均有ax(2-lnx)≤1，求实数a的取值范围.

(2)是一个恒成立问题，首先想到的是求函数g(x)=ax(2-lnx)在区间(0,+∞)的最大值.但求导发现，无法顺利求出函数g(x)的最大值，因而解题受阻.

法二：利用本题第一小题的结论解题