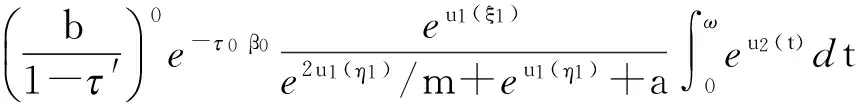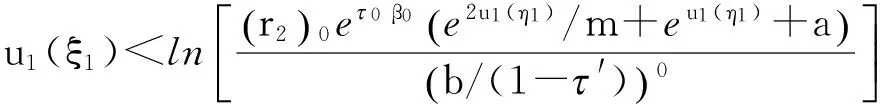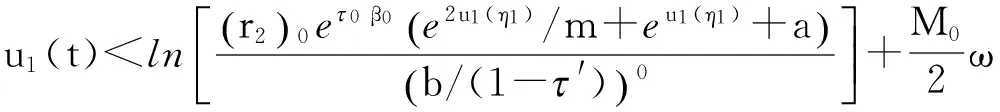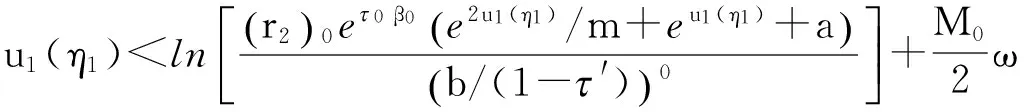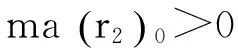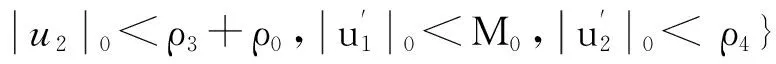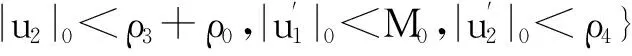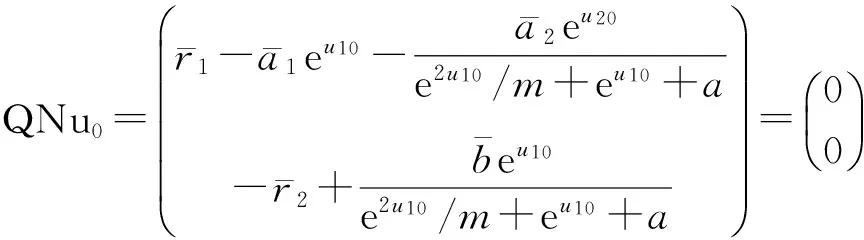具有阶段结构的中立型捕食系统的正周期解

姚晓洁， 秦发金

(广西科技师范学院数学与计算机科学学院，来宾 546100)

具有阶段结构的中立型捕食系统的正周期解

姚晓洁*， 秦发金

(广西科技师范学院数学与计算机科学学院，来宾 546100)

研究具有功能反应和时滞阶段结构的中立型捕食系统存在多个正周期解有着非常重要的意义. 提出了一类具有HollingIV类功能反应和时滞阶段结构的中立型捕食系统. 通过利用重合度理论中的延拓定理和一些不等式分析技巧,细致分析系统的解的界,给出了2种可能情形,获得了该系统至少存在2个正周期解的充分条件.

HollingIV类功能反应; 时滞阶段结构； 中立型捕食系统； 多个正周期解； 重合度

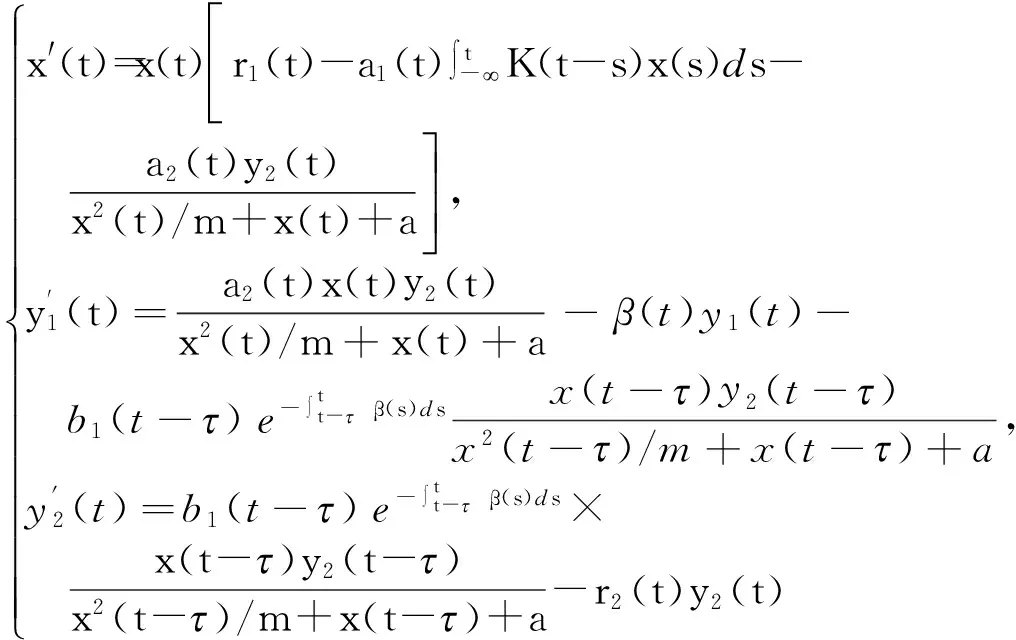
(1)

的周期解问题，利用重合度理论和不等式分析技巧，获得了系统(1)至少存在2个正周期解的充分条件. 另一方面,对中立型捕食系统周期解的研究也引起许多学者的广泛关注[6-10]. 虽然，对生物种群系统具有多个正周期解的研究有许多结果[11-13]，但自然界中生物种群的增长一般都要经历一个生长的发育过程，且在不同的生长阶段可能会有不同的特性，因此，研究具有阶段结构和功能反应的中立型捕食系统的多个周期解具有十分重要的意义. 目前对具有阶段结构的中立型生物种群系统具有多个周期解却很少研究成果，因此，本文在文献[4]的基础上加入中立型项，研究如下一类具有第Ⅳ类功能反应的时滞阶段结构时滞中立型捕食系统的周期解的存在性问题，其中x(t)表示食饵种群在时刻t的密度，y1(t)和y2(t)分别表示捕食者种群的幼年和成年在时刻t的密度，r1(t)、a1(t)、a2(t)、b(t)、r2(t)、β(t)、、σ和δ都是连续的正ω-周期函数，ω>0、m>0、a>0均为常数，b(t-表示幼年捕食者从时刻t-(t)到时刻t转化为成年捕食者的数量，q,δC1(R,[0,+)),σC2(R,R). 系统(2)的初始条件为

(2)

x(t)=φ(t),yi(t)=φi(t)(i=1,2;-θ≤t≤0),

φ(0)>0,φi(0)>0,φ,φiC1([-θ,0],[0,))

(i=1,2),

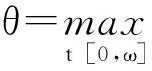
为了方便研究，对任意连续ω-周期函数f(t)，我们引入下列记号：

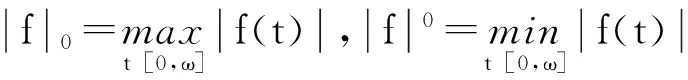
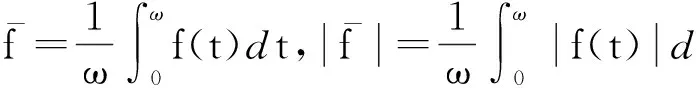
本文总假设：

(A1)σ′(t)<1,δ′(t)<1,′(t)<1，且φ(t)>0，这里φ1(p)是p=t-δ(t)的反函数.

(A2)eBq0<1，这里

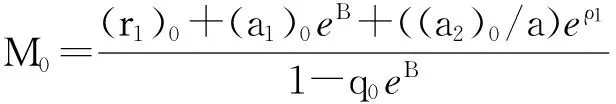
1 准备知识

为得到本文的结果，先引入Mawhin延拓定理.

设X和Z是赋范向量空间，L:DomL⊂X→Z为线性映射，N:X→Z为连续映射，如果dimKerL=codimImL<+，且ImL为Z中的闭子集，则映射L称为零指标的Fredholm映射. 如果L是零指标的Fredholm映射，且存在连续投影P:X→X及Q:Z→Z使得ImP=KerL，ImL=KerQ=Im(I-Q)，则可逆，设其逆映射为KP. 设Ω为X中有界开集，若QN()有界且KP(I-Q)N:→X是紧的，则称N在上是L-紧的. 由于ImQ与KerL同构，因而存在同构映射J:ImQ→KerL.

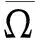
(i)对任意的(0,1)，方程Lx=N(x)的解满足x∂Ω；

(ii)QNx≠0,∀x∂Ω∩KerL；

(iii)deg{JQNx,Ω∩KerL}≠0.

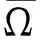
引理2[15]设gC1(R,R)且g(t)=g(t+ω)，则

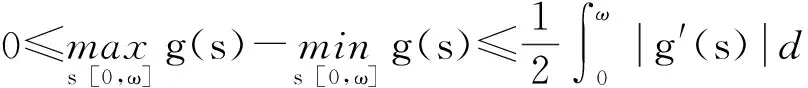
引理3[4]若α(t)和g(t)是ω-周期函数，则系统y′(t)=α(t)y(t)+g(t)有唯一的周期解，且此周期解可表示为

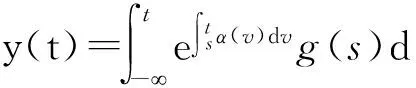
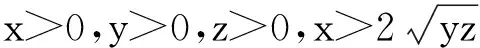
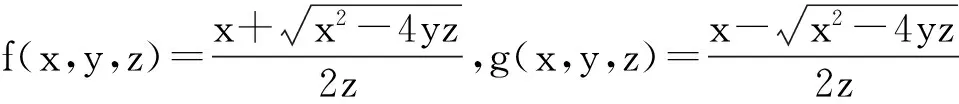
有下列结论:

(i)f(x,y,z)和g(x,y,z)在x[0,+)上关于x分别是单调递增和单调递减的;

(ii)f(x,y,z)和g(x,y,z)在y[0,+)上关于x分别是单调递减和单调递增的;

(iii)f(x,y,z)和g(x,y,z)在z[0,+)上关于x分别是单调递减和单调递增的.

为了方便证明,引进如下正数:

2(r2)0,

2(r2)0,

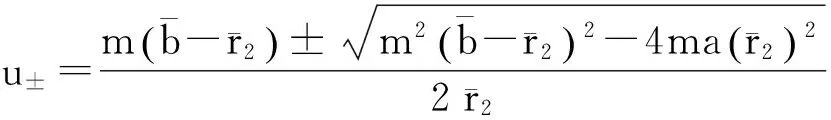
注意到系统(2)的第1、3个方程可以从整个系统分离出来，因此，我们考虑系统(2)的如下子系统

(3)

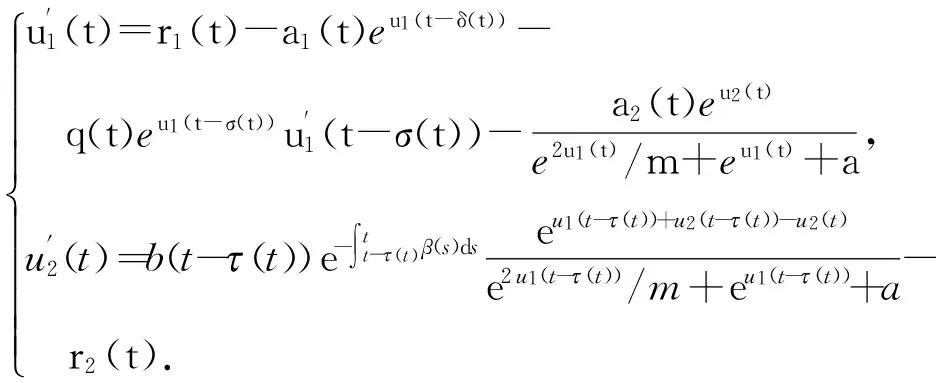
(4)

取X={u=(u1(t),u2(t))TC1(R,R2):ui(t+ω)=ui(t),tR,i=1,2}，Z={u=(u1(t),u2(t))TC(R,R2):ui(t+ω)=ui(t),tR,i=1,2}. 定义‖u‖1=,‖u‖，则X和Z在范数‖·‖1和‖·‖都是Banach空间.

定义

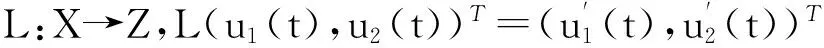
N:X→Z,Nu=

易知P和Q是连续的投影且使得ImP=KerL,KerQ=ImL=Im(I-Q)，从而，广义逆(L)KP:ImL→KerP∩DomL是

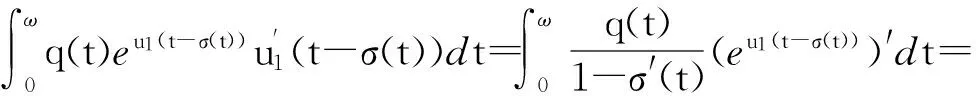
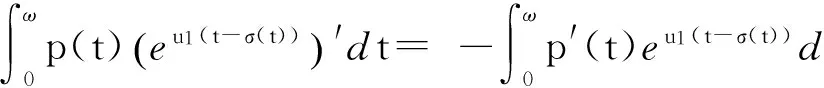
(5)

则

QNu=

KP(I-Q)N(u)=

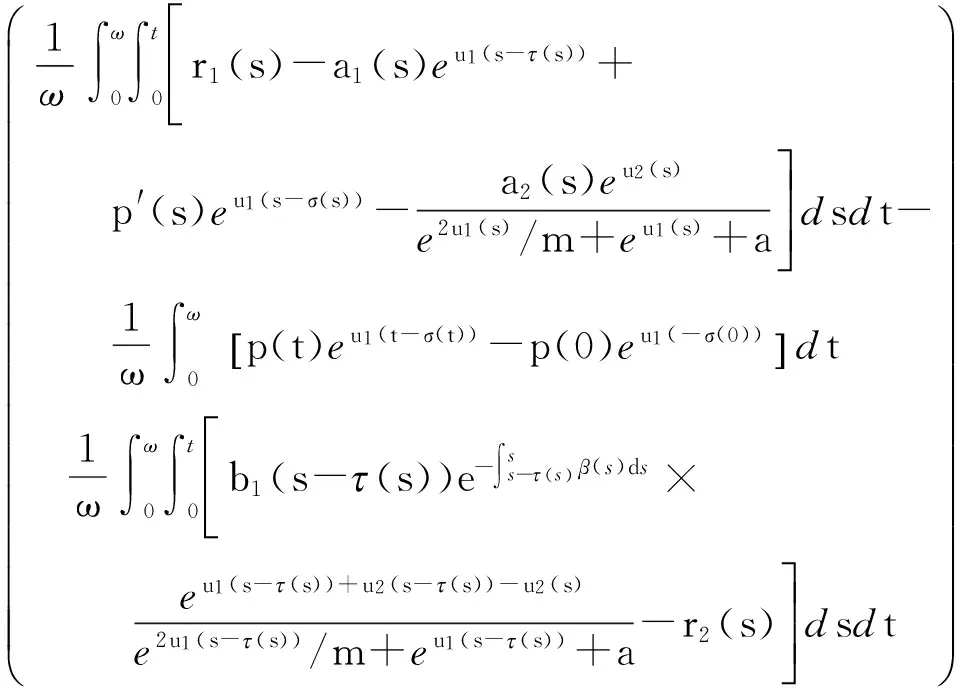
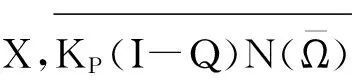
2 主要结果

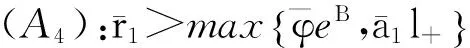
证明 根据前面的分析,我们只需证明系统(4)周期解的存在性.考虑算子方程Lu=Nu，(0,1)，即

(6)

假设(u1(t),u2(t))TX是式(6)相应于某个(0,1)的解，结合式(5)，将式(6)从0到ω积分得

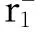
(7)

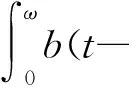
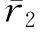
(8)

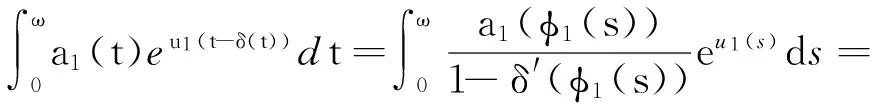
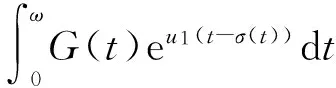
结合式(7)可得

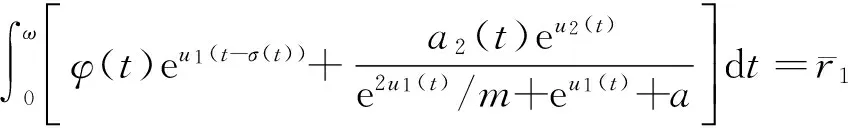
(9)

从而由式(6)及式(9)可得

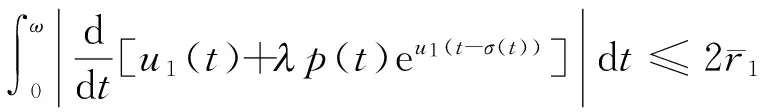
(10)

由式(9)可得

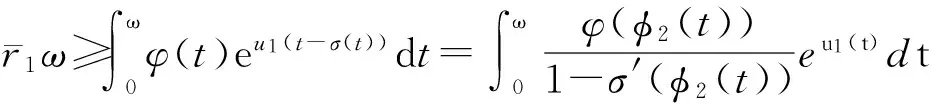
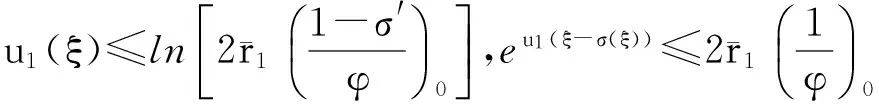
(11)

由式(9)、(10)和引理2可得

u1(t)+p(t)eu1(t-σ(t))≤u1(ξ)+p(ξ)eu1(ξ-σ(ξ))+

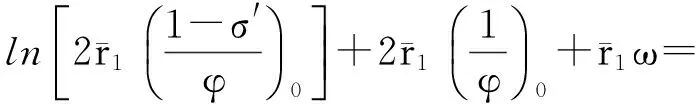
u1(t)≤B,∀t[0,ω].

(12)

由式(6)、(8)可得

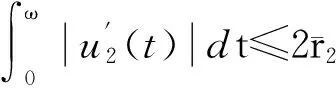
(13)

由于(u1(t),u2(t))TX，则可选择ξi,ηi[0,ω](i=1,2)，使得

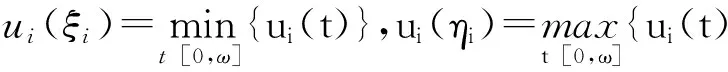
(14)

由式(9)、(12)和式(14)可得

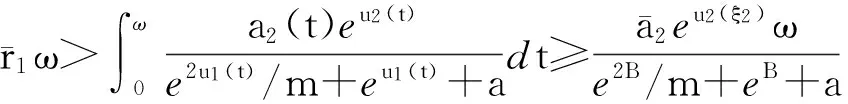
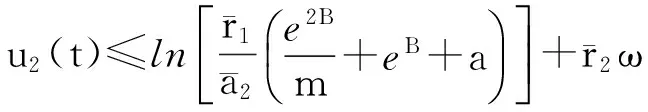
(15)

再由式(9)、(12)和式(14)可得

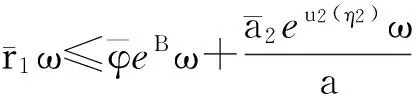
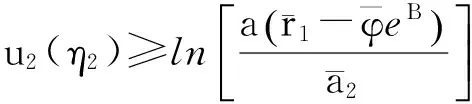
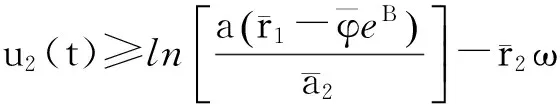
(16)

由式(15)、(16)可得

(17)

由式(6)、(11)和式(15)得

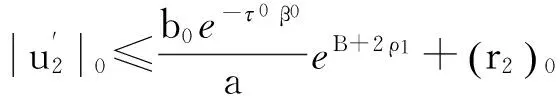
(18)

由式(6)、(11)和式(15)可得

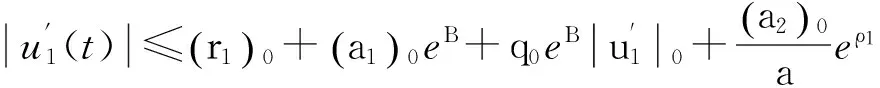
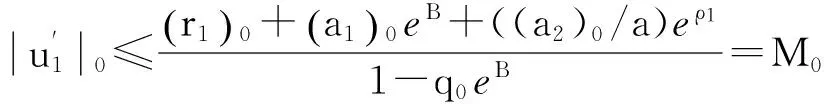
(19)

由式(6)的第2个方程可得

(20)

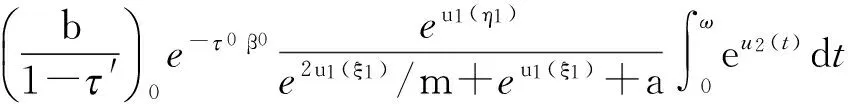
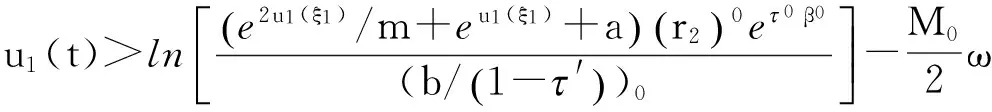
特别有

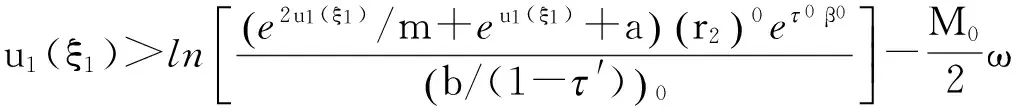
也即

这意味着

lnl-

(21)

再由式(14)、(20)得

特别有

这意味着u1(η1)lnh+. 显然，l±、h±、ρ3、ρ4、M0、B与选取无关. 定义

Ω1={u=(u1,u2)TX|u1(t)(lnl-,lnh-),

Ω2={u=(u1,u2)TX|u1(t)(lnh+,max{lnl+,B}),

显然,Ωi(i=1,2)是X上的有界开集,且Ωi∩Ωj=∅(i≠j),从而Ωi(i=1,2)满足引理1的条件(i). 现在证明引理1的条件(ii)也成立，即证若u∂Ωi∩KerL=∂Ωi∩R2时有QNu≠0. 用反证法. 假设存在u0=(u10,u20)T∂Ωi(i=1,2),使得QNu0=0,即

(22)

显然，根据定理1的条件可知，方程(22)有2个不同的解：

直接计算可得

[1] 陈凤德,陈晓星,张惠英. 捕食者具有阶段结构Holling Ⅱ类功能性反应的捕食模型正周期解的存在性以及全局吸引性[J]. 数学物理学报,2006,26A(1):93-103.

CHEN F D,CHEN X X,ZHANG H Y. Positive periodic solutions of delayed predator-prey system with Holling type Ⅱ functional response and stage structure for predator [J]. Acta Mathematica Scientia,2006,26A(1):93-103.

[2] 秦发金. 一类具有收获率和扩散的时滞阶段结构捕食系统的多重正周期解[J]. 数学物理学报,2009,29A(6):1613-1622.

QIN F J. Multiple periodic solutions for a delayed stage-structure predator-prey systems with harvesting rate and diffusion[J]. Acta Mathematica scientia,2009,29A(6):1613-1622.

[3] 秦发金,姚晓洁,黄燕革. 一类具有收获率的时滞阶段结构捕食系统的多重正周期解[J]. 数学的实践与认识,2010,40(4):120-127.

QIN F J,YAO X J,HUNAG Y G. Multiple periodic solutions for a delayed stage-structure predator-prey systems with harvesting rate[J]. Mathematics in Practice and Theory,2010,40(4):120-127.

[4] XIA Y H,CAO J D,CHENG S S. Multiple periodic solutions for a delayed stage-structure predator-prey model with non-monotone functional response[J]. Applied Mathematical Modelling,2007,31:1947-1959.

[5] 高巧琴,雒志江. 一类具有时滞和基于比率的阶段结构捕食扩散模型[J]. 生物数学学报,2014,29(1):136-142. GAO Q Q, LUO Z J. Astage-structure predator-prey diffusive system with time delays and ratio-dependent[J].Journal of Biomathematics,2014,29(1):136-142.

[6] 陈凤德,陈晓星,林发兴,等. 一类具有功能性反应的中立型捕食者-食饵系统全局正周期解的存在性[J]. 数学物理学报,2005,25A(7):981-989.

CHEN F D,CHEN X X,LIN F X,et al. Global existence of positive periodic solution of a neutral type predator-prey system with Holling Ⅱ functional response[J]. Acta Mathe-matica Scientia,2005,25A(7):981-989.

[7] 李建东. 具有比率依赖的中立型捕食-被捕食系统的周期正解[J]. 数学的实践与认识，2014,44(6):279-284.

LI J D. Positive periodic solutions to neutral ratio-dependentpredator-prey system[J]. Mathematics in Practice and Theory,2014,44(6):279-284.

[8] 姚晓洁,秦发金. 具有比率和单调功能反应的中立型捕食系统的正周期解[J]. 数学的实践与认识,2014,44(3):274-280.

YAO X J,QIN F J. Positive periodic solutions for a kind of neutralpredator-prey system with ratio-dependent and monotonic functional response[J]. Mathematics in Practice and Theory,2014,44(3):274-280.

[9] LIU G,YAN W,YAN J. Positive periodic solutions for a class of neutral delay Gause-type predator-prey system[J].Nonlinear Anal,2009,71:4438-4447.

[10] 李志宏. 比率依赖的中立型Holling-Tanner的周期正解[J]. 太原师范学院学报(自然科学版),2014,13(2):29-34.

LI Z H. Existence of positive periodic solution of neutral Holling-Tanner functional response[J]. Journal of Taiyuan Normal University(Nature Science Edition),2014,13(2):29-34.

[11] 姚晓洁. 具有收获率和2个功能反应的捕食系统的多个正周期解[J]. 华南师范大学学报(自然科学版),2015,47(6):105-110.

YAO X J. Multiple positive periodic solutions for predator-prey system with harvesting terms and two functional responses[J]. Journal of South China Normal University(Nature Science Edition),2015,47(6):105-110.

[12] 刘子珍,刘秀湘. 具有迁移效应和收获率的Hassell-Varley-Holling 捕食者一食饵系统的周期解[J]. 华南师范大学学报(自然科学版),2014,46(2):10-16.

LIU Z H,LIU X X. Periodic solutions in a Hassel-Varley-Holling predator-prey system with dispersal and harves[J]. Journal of South China Normal University(Nature Science Edition),2014,46(2):10-16.

[13] 魏凤英. 具Ⅱ类功能反应及捕获的两斑块扩散捕食系统多个周期解的存在性[J]. 东北师大学报(自然科学版),2012,44(3):9-14.

WEI F Y. Existence of multiple positive periodic solutions for two-patch diffusive predator-prey system with harvesting and HollingⅡtype functional respons[J]. Journal of Northeast Normal University(Nature Science Edition), 2012,44(3):9-14.

[14]GAINES R E,MAWHIN J L. Coincidence degree and nonlinear differential equation[M]. New York:Springer,1977.

[15]WANG Q,DAI B X,CHEN Y M. Multiple periodic solutions of an impulsive predator-prey model with Holling-type IV functional response[J]. Mathematical & Computer Modelling,2009,49(9/10):1829-1836.

[16]ZHAO K H,YE Y. Four positive periodic solutions to a periodic Lotka-Volterra predatory-prey system with harvesting terms[J]. Nonlinear Analysis:Real World Applications,2010,11(4):2448-2455.

【中文责编：庄晓琼 英文责编:肖菁】

PositivePeriodicSolutionsofNeutralPredator-PreySystemswithStageStructure

YAO Xiaojie*， QIN Fajin

(College of Mathematics and Computer Science, Guangxi Science & Technology Normal University, Laibin 546100， China)

It is very important to study the existence of multiple positive periodic solutions of neutral predator prey systems with functional response and delay stage structure. A system is proposed to a neutral predator-prey system with Holling type IV functional response and time delay and stage structure. By using a continuation theorem based on coincidence degree theory and some inequality analysis techniques, the bounds of solutions of this system are analyzed in detail. Two possible cases are given and some sufficient conditions of the at least two positive periodic solutions for the system are established.

Holling IV functional response; delayed stage structure; neutral predator-prey system; multiple positive periodic solution; coincidence degree

2015-10-16 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

广西壮族自治区自然科学基金项目(2013GXNSFAA019022)；广西壮族自治区高校科学技术研究项目(YB2014468,2013YB282,2013YB243)

O

A

1000-5463(2017)03-0102-07

*通讯作者:姚晓洁，副教授，Email:yaoxiaojie1970@163.com.