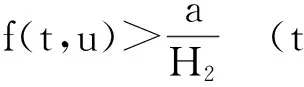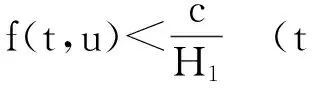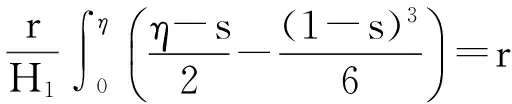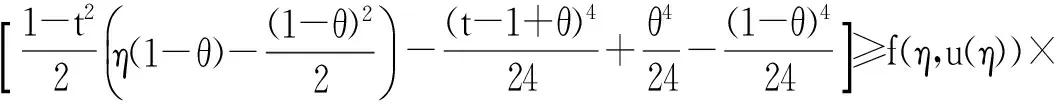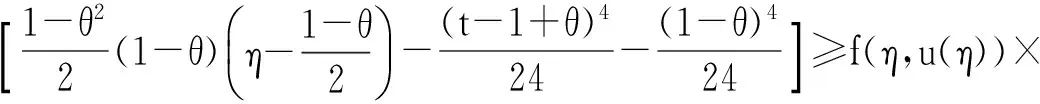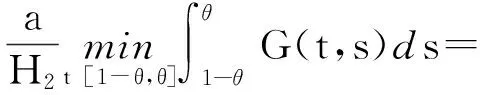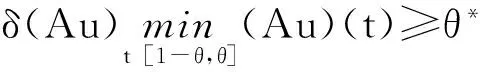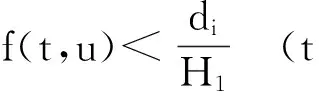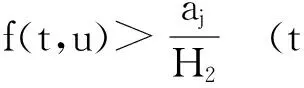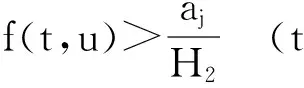带变号格林函数的四阶三点边值问题的多个正解的存在性
达举霞, 霍 梅, 韩晓玲
(西北师范大学数学与统计学院, 兰州 730070)
带变号格林函数的四阶三点边值问题的多个正解的存在性
达举霞, 霍 梅, 韩晓玲*
(西北师范大学数学与统计学院, 兰州 730070)
应用Leggett-Williams不动点定理研究了四阶三点边值问题
多个正解的存在性,其中f:[0,1]×[0,+∞)→[0,+∞)连续,η为常数. 尽管Green函数是变号的,对任意的正整数m,该问题仍有正解且至少有2m-1个正解.
四阶三点边值问题; 变号Green函数; 多个正解
u(4)(t)=f(t,u(t)) (t[0,1]),
u′(0)=u″(η)=u‴(0)=u(1)=0,
wheref:[0,1]×[0,+∞)→[0,+∞) is continuous,η.Theexistenceofatleast2m-1positivesolutionsforarbitrarypositiveintegermisobtainedwhiletheproblemhasthesign-changingGreen’sfunction.
Keywords:fourth-orderthree-pointboundaryvalueproblem;sign-changingGreen’sfunction;multiplepositivesolutions
弹性梁是工程建筑的基本构件,弹性力学和工程物理常用四阶常微分方程边值问题来刻画弹性梁的平衡状态,由于这类问题的普遍性和重要性,四阶两点边值问题和四阶多点边值问题深受学者关注.
2008年,YAO[1]运用Krasnoselskli不动点定理获得了四阶三点边值问题
u(4)(t)+F(t,x(t),x″(t))=0 (t[0,1]),
x″(0)=x″(1)=0,x(η)=B,x′(η)=C (0<η<1)
n个正解的存在性结果.
2009年,GRAEF等[2]运用锥上的不动点定理研究了四阶三点边值问题
u(4)(t)=g(t)f(u(t)) (t[0,1]),
(1)
u(0)=u′(0)=u″(β)=u‴(1)=0
(2)
2014年,ZHOU等[3]运用不动点指数理论获得了四阶三点边值问题
u(4)(t)=g(t)f(u(t)) (t[0,1]),
u(0)=u′(0)=u″(β)=u″(1)=0
以上结果都是在Green函数非负的情况下获得的. 2012年,SUN和ZHAO[4]运用Leggett-Williams不动点定理在Green函数变号时获得了问题
u‴(t)=f(t,u(t)) (t[0,1]),
u′(0)=u″(η)=u(1)=0多个正解的存在性结果,这里fC([0,1]×[0,+∞)),η).
更多详细结果见文献[5-11]. 受前人启发,本文在Green函数变号的情况下运用Leggett-Williams不动点定理研究问题
(3)多个正解的存在性,这里fC([0,1]×[0,+∞),[0,+∞)),η,推广了文献[4]的主要结果.
1 预备知识
设E是Banach空间,P是E上的锥. 对任意的x,yP,t[0,1],若有δ(tx+(1-t)y)≥tδ(x)+(1-t)δ(y),则映射δ:P→(-∞,+∞)是一个凹函数. 设a和b是2个常数且0 Pa={xP:‖x‖≤a}, P(δ,a,b)={xP:a≤δ(x),‖x‖≤b}. (2)‖Ax‖ ‖x1‖ u″(t)≤0,t[0,η]; u″(t)≥0,t[η,1]. (5)在 u(1)≤0的情况下,由式(5)可知u′(t)≤0,t[0,1], u(1)=0 ,这意味着 u(t)≥0,t[0,1]. 因此,在 E 上定义一个锥如下:E:u(t)≥0且u单调递减,t[0,1],u′(1)≤0}. u(4)(t)=y(t) (t[0,1]), (6) u′(0)=u″(η)=u‴(0)=u(1)=0. 在[0,t]上给式(6)两边积分,得到 (7) 在[0,t]上给式(7)两边积分,得到 (8) 继续在[0,t]上给式(8)两边积分,得到 (9) 最后再在[0,t]上给式(9)两边积分,得到 从而式(6)的格林函数的表达式G(t,s)如下: (1)当s≥η时,有 max{G(t,s):t[0,1]}=G(1,s)=0; 对于s<η,有 max{G(t,s):t. 可得 则 本文假定f:[0,1]×[0,+∞)→[0,+∞)是连续的并且满足如下条件: (C1)对每一个x[0,+∞),映射t→f(t,x)是递减的; (C2)对每一个t[0,1],映射 x→f(t,x)是递增的. 显然,如果u是A在P上的不动点,则u是式(3)的非负解. 为了方便,记 定理2 设存在数d、a和c,0 (10) (11) (12) (13) 综上,Leggett-Williams不动点定理的所有条件都被满足. 因此,A至少有3个不动点,即式(3)至少有3个正解u、v和w并满足 定理3 设m是任意正整数,假设存在di(1≤i≤m)和aj(1≤j≤m-1),且0 (14) (15) (16) 例1 考虑BVP u(4)(t)=f(t,u(t)) (t[0,1]), (18) (19) 其中 f(t,u)= [1]YAOQL.Existenceandmultiplicityofpositivesolutionstononlinearfourth-orderthree-pointboundaryvalueproblem[J].JournalofZhejiangUniversity,2008,35:378-380. [2]GRAEFJR,HENDERSONJ,YANGB.Positivesolutionstoafourthorderthreepointboundaryvalueproblem[J].DiscreteandContinuousDynamical,2009,285:269-275. [3]ZHOUSH,WUHP,HANXL.Existenceofpositivesolutionsofthefourth-orderthree-pointboundaryvaluepro-blems[J].JournalofSichuanUniversity,2014,51:11-15. [4]SUNJP,ZHAOJ.Multiplepositivesolutionsforathird-orderthree-pointBVPwithsign-changingGreen’sfunction[J].JournalofMathematicalAnalysisandApplications,2012(118):1-7. [5]LEGGETTRW,WILLIAMSLR.MultiplepositivefixedpointsofnonlinearoperatorsonorderedBanachspaces[J].IndianaUniversityMathematicsJournal,1979,28(4):673-688. [6]SUNJP,ZHAOJ.Iterativetechniqueforathird-orderthree-pointBVPwithsign-changingGreen’sfunction[J].JournalofMathematicalAnalysisandApplications,2013,215:1-9. [7]SUNYP.Positivesolutionsforthird-orderthree-pointnonhomogeneousboundaryvalueproblems[J].AppliedMathematicsLetters,2009,22(1):45-51. [8] 达佳丽,韩晓玲. 三阶三点边值问题3个正解的存在[J]. 华南师范大学学报(自然科学版),2015,47(3):148-150. DAJL,HANXL.Existenceofthreepositivesolutionsforathird-orderthree-pointboundaryvalueproblem[J].JournalofSouthChinaNormalUniversity(NaturalScienceEdition),2015,47(3):148-150. [9]YAOQL.Theexistenceandmultiplicityofpositivesolutionsforathird-orderthree-pointboundaryvaluepro-blem[J].JournalofMathematicalAnalysisandApplications,2003,288:1-14. [10]FENGXF,FENGHY,BAIDL.Eigenvalueforasingularthird-orderthree-pointboundaryvalueproblem[J].AppliedMathematicsandComputation,2013,219(18):9783-9790. [11]DUZJ,GEWG,LINXL.Existenceofsolutionsforaclassofthird-ordernonlinearboundaryvalueproblems[J].JournalofMathematicalAnalysisandApplication,2004,294(1):104-112. 【中文责编:庄晓琼 英文审校:肖菁】 Existence of Multiple Positive Solutions for A Fourth-Order Three-Point BVP with Sign-Changing Green’s Function DAJuxia,HUOMei,HANXiaoling* (College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China) By applying Leggett-Williams fixed point theorem,the fourth-order three-point boundary value problem is studied: 2015-11-20 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n 国家自然科学基金项目(11561063) u(4)(t)=f(t,u(t)) (t[0,1]), u′(0)=u″(η)=u‴(0)=u(1)=0 O175.8 A 1000-5463(2017)03-0109-05 *通讯作者:韩晓玲,教授,Email:hanxiaoling9@163.com.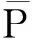
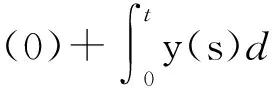



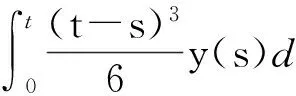

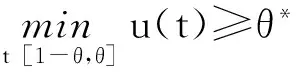
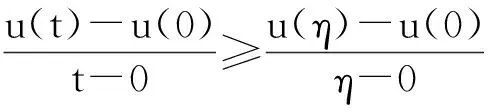

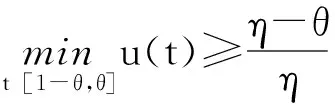
2 主要结果