一类解析函数的Fekete-Szegö不等式

郭 栋， 李宗涛

(1. 滁州职业技术学院基础部，滁州 239000； 2. 广州民航职业技术学院基础部，广州 510403)

一类解析函数的Fekete-Szegö不等式

郭 栋1*， 李宗涛2

(1. 滁州职业技术学院基础部，滁州 239000； 2. 广州民航职业技术学院基础部，广州 510403)

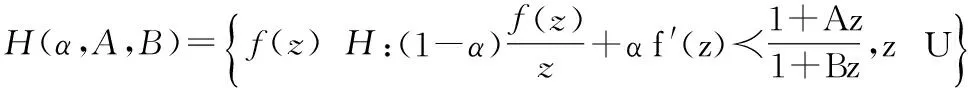
单叶函数; H(α,A,B)函数;Fekete-Szegö不等式

Keywords：univalentfunction; H(α,A,B)function;Fekete-Szegöinequality

令H表示形如

f(z)=z+a2z2+a3z3+…

(1)

FEKETE和SZEGÖ[1]证明了：设f(z)S， f(z)由式(1)给出，0≤u<1，则

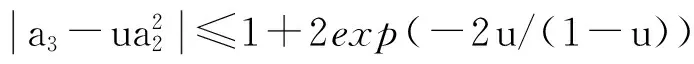
且对每个u等号都成立.

1994年,何维明[2]引入了函数类

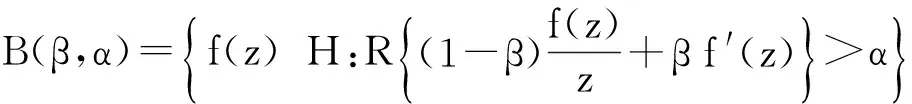
并且研究了此函数类的Fekete-Szegö不等式.

仿照函数类B(β,α),本文定义函数类H(α,A,B)：

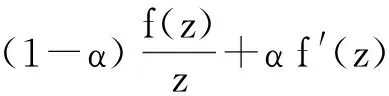
(2)

记函数f(z)H(α,A,B),其中幂函数取主值.

当函数类H(α,A,B)的参数取一些特殊值时,就得到我们熟知的函数类,例如[2-3]：

(1)当A=1-2ρ,B=-1时,

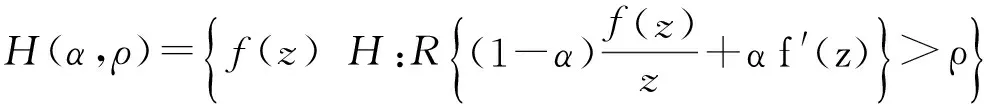
其中0≤ρ<1.

(2)当A=1-2α,B=-1,α=β时, H(β,1-2α,-1)=B(β,α).

(3)当A=1-2α,B=-1,α=1时,H(1,1-2α,-1)=P(α).

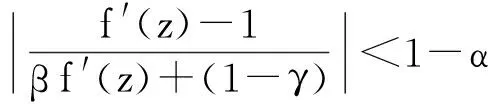
文献[5-9]研究了H中一些子类的Fekete-Szegö问题. 本文利用施瓦兹函数的Fekete-Szegö不等式，得到了H(α,A,B)上的Fekete-Szegö不等式，并推广了一些结果.

引理1[10]设ω(z)=d1z+d2z2+…在zU时解析,且|ω(z)|≤|z|,则对任意的复数t,有}. 等号在函数ω(z)=z2和ω(z)=z时成立.

引理2[11]设ω(z)=d1z+d2z2+…在zU时解析,且|ω(z)|≤|z|,则对任意的实数t有

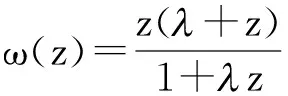
和

引理3[12]设p(z)=1+p1z+p2z2+…在U={z:|z|<1}内解析且满足Rep(z)>0，则

下面给出本文的主要结果及证明.

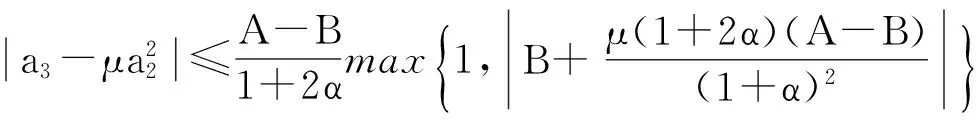
且对所有的μ等号都成立.

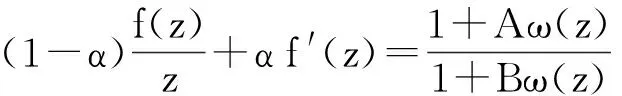
(3)

将f(z)、ω(z)的幂级数展开式代入式(3)，并比较恒等式两边z和z2两项的系数，可得

(4)

所以

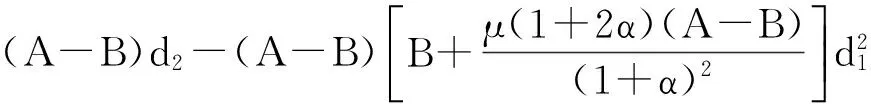
(5)

当α≠0时，相应的极值函数为

或

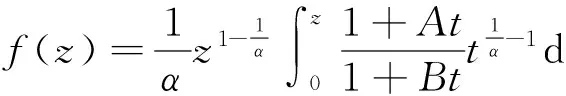
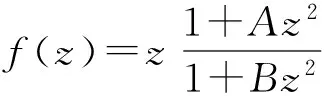
且对所有的μ等号都成立.

注1 推论1中令α=β,ρ=α，H(α,ρ)就变为文献[2]的函数类B(β,α)，μ由实数推广到复数.

由定理1的证明过程及引理2可得：

若μ1≤μ≤μ2，由引理2，定理2可以改进为：

且对所有的μ等号都成立，其中μ3=-B(1+α)2/[(A-B)(1+2α)].

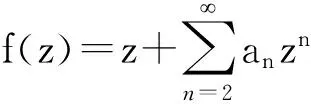
且对所有的μ等号都能成立.

类似于定理1的证明,可以证明定理4,此处略.

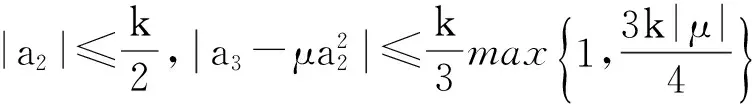
且对所有的μ等号都能成立.

注2 推论2中令k=1，得文献[4]中R(0,0,0)的Fekete-Szegö不等式.

[1]FEKETEM,SZEGÖG.EineBermerkunguberungeradeschlichtefunktionen[J].JournaloftheLondonMathematicalSociety,1933,8(1):85-89.

[2] 何维明. 某族解析函数的Fekete-Szegö不等式[J]. 长沙交通学院学报,1994,10(3):13-17.

HEWM.TheFekete-Szegöinequalytiesforcertainclassanalyticfunctions[J].JournalofChangshaCommunicationsInstitute,1994,10(3):13-17.

[3]OWAS,AOUFMK,NASRMA.Noteoncertainsubclassofclose-to-convexfunctionsoforderα[J].InternationalJournalofMathematics&MathematicalSciences,1990,13(1):189-192.

[4] 高纯一. 近于凸函数族的一个子类[J]. 长沙交通学院学报,1994,10(4):1-7.

GAOCY.Asubclassofclose-to-convexfunctions[J].JournalofChangshaCommunicationsInstitute,1994,10(4):1-7.

[5]LIUMS.Oncertainclassofanalyticfunctionsdefinedbydifferentialsubordination[J].ActaMathematicaScientia,2002,22B(3):388-392.

[6] 刘名生,崔志峰. 一类解析函数子类的Fekete-Szegö不等式[J]. 华南师范大学学报(自然科学版)，2010(1):1-4.

LIUMS,CUIZF.Fekete-Szegöinequalitiesforsomesubclassesofanalyticfunctions[J].JournalofSouthChinaNormalUniversity(NaturalScienceEdition),2010(1):1-4.

[7] 鲍春梅,李书海. 一类β级扩展的Bazilevic函数及其Fekete-Szegö问题[J]. 华南师范大学学报(自然科学版)，2010(3):7-10.

BAOCM,LISH.AclassofβrankexpandedBazilevicfunctionandFekete-Szegöproblem[J].JournalofSouthChinaNormalUniversity(NaturalScienceEdition),2010(3):7-10.

[8] 郭栋,李宗涛,杨家稳. 一类解析函数类的Fekete-Szegö问题[J]. 华南师范大学学报(自然科学版)，2012,44(4):28-30.

GUOD,LIZT,YANGJW.TheFekete-Szegöinequlitityforsomesubclassesanalyticfunctions[J].JournalofSouthChinaNormalUniversity(NaturalScienceEdition),2012,44(4):28-30.

[9] 崔志峰,刘名生. 用卷积定义的解析函数子类的Fekete-Szegö不等式[J]. 数学杂志，2011，31(5):954-961.CUIZF,LIUMS.Fekete-Szegöinequalitiesforcertainsubclassesofanalyticfunctionsdefinedbyconvolution[J].JournalofMathematics,2011,31(5):954-961.

[10]KEOGHFR,MERKESEP.Acoefficientinequalityforcertainclassofanalyticfunctions[J].ProceedingsoftheAmericanMathematicalSociety,1969,20:8-12.

[11]PROKHOROVDV,SZYNALJ.Inversecoefficientsfor(α,β)-convexfunctions[J].AnnalesUniversitatisMariaeCurie-SklodowskaA,1981,35:125-143.

[12] 刘名生. 某类解析函数的Fekete-Szegö不等式[J]. 数学物理学报,2002,22A(1):8-14.

LIUMS.TheFekete-Szegöinequalityforcertainclassofanalyticfunctions[J].ActaMathematicaScientia,2002,22A(1):8-14.

【中文责编：庄晓琼 英文责编：肖菁】

TheFekete-SzegöInequalityforASubclassofAnalyticFunctions

GUODong1*，LIZongtao2

(1. Foundations Department, Chuzhou Vocational and Technical College, Chuzhou 239000, China；2. Foundations Department, Guangzhou Civil Aviation College, Guangzhou 510403, China)

2016-01-12 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

安徽省高校自然科学基金重点资助项目(KJ2015A372)

O

A

1000-5463(2017)03-0114-03

*通讯作者:郭栋，副教授,Email：Gd791217@163.com.