高阶多元Markov链联合稳定分布向量的扰动界

郑 华, 林彩凤, 祝长华*

(1. 韶关学院数学与统计学院, 韶关 512005;2. 华南师范大学数学科学学院, 广州 510631)

高阶多元Markov链联合稳定分布向量的扰动界

郑 华1, 林彩凤2, 祝长华1*

(1. 韶关学院数学与统计学院, 韶关 512005;2. 华南师范大学数学科学学院, 广州 510631)

给出了高阶多元Markov链联合稳定分布向量的几个扰动界:结合高阶多元Markov链概率转移矩阵左、右特征向量的相关性质,得到高阶多元Markov链联合稳定分布向量的扰动界,新的扰动界结果是一阶多元Markov链联合稳定分布向量扰动界结果的推广;利用高阶多元Markov链概率转移矩阵的特殊性,给出其联合稳定分布向量可计算形式的扰动界,也是已有一阶多元Markov 链联合稳定分布向量相应扰动界结果的推广;结合Paz不等式,通过分析高阶多元Markov链联合稳定分布向量的分量扰动,得到了联合稳定分布向量基于分量形式的扰动界,便于观察高阶多元Markov 链中具体某条链某个状态的扰动.

高阶多元Markov链; 联合稳定分布向量; 扰动界

Markov链模型[1]在现实生活中已经广泛地应用于各个领域,如排队模型[2]、工业系统[3]和存储系统[4]等. 在许多实际应用问题中,往往需要对几类数据进行分析,即同时考虑多条Markov链,称多元Markov链[5],简化的多元Markov链模型也广泛应用于各个领域,如市场需求预测[4]、基因布尔网络的建立[6]等. 进一步地，还需要考虑多步之间的关系和刻画各条链之间、每条链内部的相互关系, 即高阶Markov 链[7]以及高阶多元Markov链[8].

Markov链模型中的参数通过解某些线性优化问题[5]或最小二乘问题[9]来估计,不同的估计方法得到不同的模型参数,从而影响模型的稳定性,因此需要分析其稳定分布向量在转移矩阵受到微小扰动后的变化,即给出扰动界. 关于Markov链联合稳定分布向量的扰动理论结果已经有很多[10-14],但关于高阶多元Markov链联合稳定分布向量的扰动分析目前还没有相关的理论结果.

本文将在文献[5]、[8]、[14]的基础上给出高阶多元Markov链联合稳定分布的3个扰动界结果,包括可计算的扰动界,并得到了分量形式的扰动界.

1 预备知识

本节回顾高阶多元Markov链模型[8]的相关概念和性质. 在后续讨论中,1l表示元素全为1的l维列向量,0l表示元素全为0的l维列向量;对于矩阵M,ρ(M)表示M的谱半径,M(i)表示矩阵M去掉第i 行后剩下的子矩阵,M*k表示矩阵M的第k列,Mk*表示矩阵M的第k行,Mj表示M去掉第j行和第j列后的顺序主子阵.

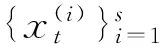
(1)

其中

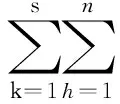
(2)

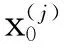
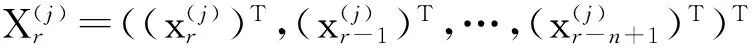
(j=1,2,…,s;r=n,n+1,…).

Xt+1=QXt,

其中

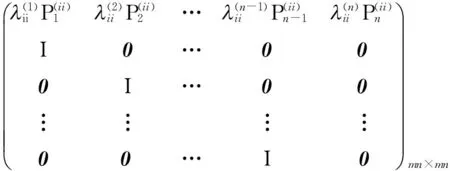
(3)

当i≠j时，有B(ij)=

(4)

此处Q称为联合转移矩阵.

注1 特别地，当n=1时，模型(1)就转化为一阶多元Markov链模型[5].

引理1[8]如果对于所有的1≤j,k≤s和1≤h≤n都有不可约,则

(i)矩阵Q有一个特征值为1,Q的模最大特征值小于等于1,且存在正向量v和u,使得

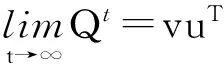
(5)

(ii)存在唯一的正向量Π,使得

QΠ=Π,‖Π‖1=ns,

(6)

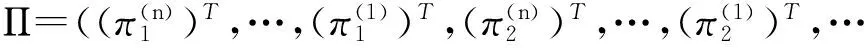
(7)

且

(8)

(iii)存在唯一正向量X,使得

XTQ=XT,‖X‖1=nm,

(9)

其中

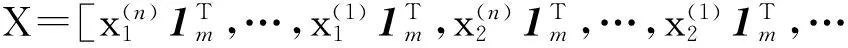
(10)

2 主要结果

首先给出高阶多元Markov链联合稳定分布向量的扰动界.

证明 由Perron-Frobenius定理,1是Q的单特征值,因此其对应的特征子空间维数是1,又X和Π分别是Q对应于1的左、右特征向量,因此存在k和l使得v=kΠ,u=lX (k,l>0),结合式(5)和式(8)有

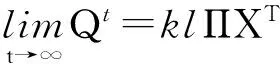
(11)

vuT=klΠXT=klQΠXT=klQtΠXT.

(kl)2nΠXT,即klΠXT=(kl)2nΠXT,因此kl=1/n,结合式(11)得：

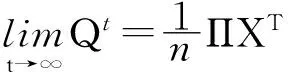
(12)

另一方面，由式(6)和式(9),用数学归纳法可得

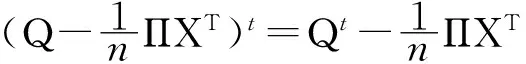
结合式(12)就有

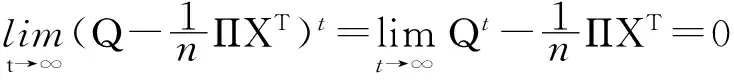
(13)

证明

由式(6)可得

(14)

结合XTΠ=n, 有

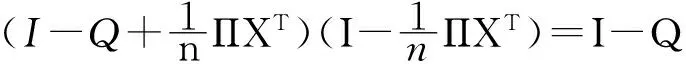
则

(15)

由式(9)易得

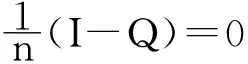
(16)

在式(14)的两边同时左乘B,结合式(15)和式(16),有

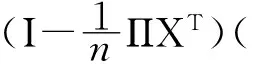
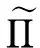
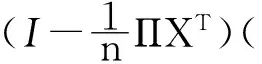
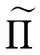
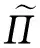
注2 定理1得到了高阶多元Markov链联合稳定分布向量的扰动界(13). 当n=1时,扰动界(13)即转化为一阶多元Markov链联合稳定分布向量的扰动界[14].

扰动界(13)中含有联合稳定分布向量的信息, 这将导致其难以计算,下面给出高阶多元Markov链联合稳定分布向量可计算的扰动界.

定义1[15]设ARn×n,并且可表示为A=sI-B(s>0,B≥0),如果s≥ρ(B),则称A为M矩阵;如果s>ρ(B),则称A为非奇异M矩阵.

引理3[15]设A是一个n阶奇异不可约的M矩阵,则A的秩为n-1,且A的所有顺序主子阵(不包含A自身)都是非奇异的M矩阵.

由引理3易得：

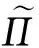
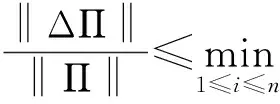
(17)

证明 从式(6)和式(8)可得：

(18)

且

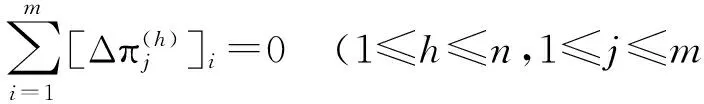
(19)

结合式(18)和式(19)有:

(20)

两边取范数后对右端取最小化即得到了式(17).证毕.

注3 当n=1时，扰动界(17)即转化为一阶多元Markov链稳定分布向量的扰动界[14].

注4 和扰动界(13)相比,扰动界(17)未包含联合稳定分布向量信息,因此是可计算的扰动界.

接下来推导基于联合稳定分布向量分量形式的扰动界.

引理5[16](Paz不等式)设zT=(z1,z2,…,zN), 如果对于n维非零向量δ,有δT1N=0,则

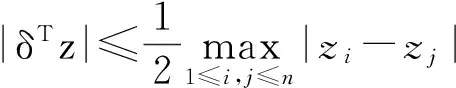
定理3 沿用和定理2相同的记号和假设,以下不等式成立:

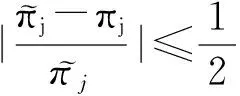
(21)

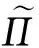
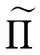
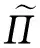
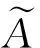
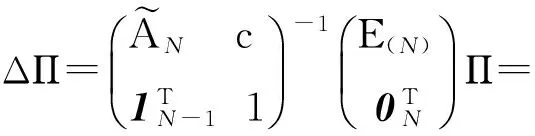
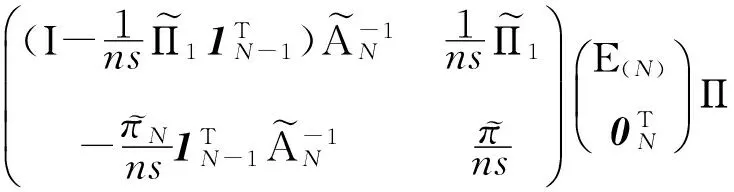
(22)

考虑式(22)的第N个元素,即得

进一步得到

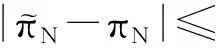
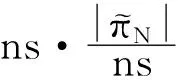
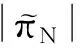
(23)

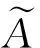
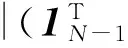
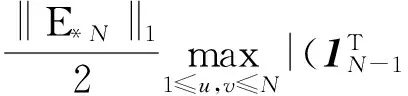
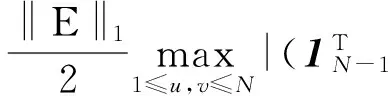
结合式(23),可得

从而式(21)成立.

注5 定理3的意义是:对于给定的某条链中的某个状态,可以由式(21)给出扰动界.

注6 式(21)也是可以计算的扰动界.

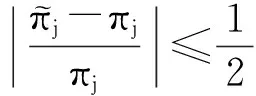
3 小结

本文给出了几个高阶多元Markov链联合稳定分布向量的扰动界,其中结合概率转移矩阵特征向量得到了扰动界(13),进一步得到可计算形式的扰动界(17),它们都是已有一阶多元Markov链相应扰动界结果的推广,最后还得到了基于分量形式的扰动界(21),极大地丰富了高阶多元Markov链的理论.

[1]CHINGWK,NGM.Markovchains[M].Berlin:Springer,2006.

[2]CHINGWK.Iterativemethodsforqueuingandmanufacturingsystems[M].Berlin:Springer,2001.

[3]BUZACOTTJA,SHANTHIKUMARJG.Stochasticmo-delsofmanufacturingsystems[M].EnglewoodCliffs:PrenticeHall,1993.

[4]CHINGWK,FUNGE,NGM.Ahigher-orderMarkovchainmodelfortheNewsboy’sproblem[J].JournaloftheOperationsResearchSociety,2003,54:291-298.

[5]CHINGWK,FUNGE,NGM.AmultivariateMarkovchainmodelforcategoricaldatasequencesanditsapplicationsindemandpredictions[J].IMAJournalofManagementMathematics,2002,13:187-199.

[6]CHINGWK,FUNGE,NGM,etal.OnconstructionofstochasticgeneticnetworksbasedonGeneexpressionsequences[J].InternationalJournalofNeuralSystems,2005,15:297-310.

[7]CHINGWK,FUNGE,NGM.Higher-orderMarkovchainmodelsforcategoricaldatasequences[J].NavalResearchLogistics,2004,51:557-574.

[8]CHINGWK,NGM,FUNGE.Higher-ordermultivariateMarkovchainsandtheirapplications[J].LinearAlgebraandItsApplications,2008,428:492-507.

[9]ZHUD,CHINGWK.MultivariateMarkovchainmodelsforproductionplanning[J].InternationalJournalofIntelligentEngineeringInformatics,2011,1:156-173.

[10]CHOG,MEYERC.ComparisonofperturbationboundsforthestationarydistributionofaMarkovchain[J].LinearAlgebraandItsApplications,2001,335:137-150.

[11]FUNDERLICR,MEYERC.PerturbationboundsforthestationarydistributionvectorforanergodicMarkovchain[J].LinearAlgebraandItsApplications,1986,76:1-17.

[12]IPSENI,MEYERC.UniformstabilityforMarkovchains[J].SIAMJournalonMatrixAnalysisandApplications,1994,15:1061-1074.

[13]KIRKLANDS,NEUMANNM,SHADERB.ApplicationsofPaz’sinequalitytoboundsforMarkovchains[J].LinearAlgebraandItsApplications,1998,268:183-196.

[14]LIW,JIANGL,CHINGWK,etal.PerturbationboundsforjointstationarydistributionsofmultivariateMarkovchainsmodels[J].EastAsianJournalonAppliedMathematics,2013,3:1-17.

[15]BERMANA,PLEMMONSRJ.Nonnegativematricesinthemathematicalsciences[M].Philadelphia:SIAM,1994.

[16]SENETAE.Non-negativematricesandMarkovchains[M].NewYork:Springer,1981.

【中文责编：庄晓琼 英文编校：肖菁】

The Perturbation Bounds of the Joint Stationary Distribution Vector of the High-Order Multivariate Markov Chains

ZHENG Hua1, LIN Caifeng2, ZHU Changhua1*

(1. School of Mathematics and Statistics, Shaoguan University, Shaoguan 512005, China;2. School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China)

The perturbation bounds of the joint stationary distribution vector of the high-order multivariate Markov chains are established. By the properties of the left and right eigenvectors of the probability transition matrix of the high-order multivariate Markov chains, the perturbation bound of the joint stationary distribution vector of the high-order multivariate Markov chains is obtained, which generalizes the results of the existing perturbation bounds of the joint stationary distribution vector of one-order multivariate Markov chains. Then the computational perturbation bound is given by the characteristic of the probability transition matrix of the high-order multivariate Markov chains, which also generalizes the corresponding perturbation bound of the joint stationary distribution vector of one-order multivariate Markov chains. Moreover, considering the perturbation in the item of the joint stationary distri-bution vector of high-order multivariate Markov chains, the perturbation bound of the joint stationary distribution vector based on component form is established by Paz’s inequality, to observe the perturbation of a state in a chain of the high-order multivariate Markov chains.

high-order multivariate Markov chains; joint stationary distribution vector; perturbation bounds

2016-09-08 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(11601340)；中山大学广东省计算科学重点实验室开放基金项目(2016005)；广东省数据科学工程技术研究中心开放基金项目(2016KF11)； 韶关学院科研项目(S201501018)

O241.1

A

1000-5463(2017)03-0092-05

*通讯作者:祝长华,讲师,Email:sguzhuchanghua@163.com.